카이제곱 분포

R2026b

개요

카이제곱(χ²) 분포는 1-모수 곡선족입니다. 카이제곱 분포는 일반적으로 가설검정, 특히 피팅의 적합도에 대한 카이제곱 검정에 사용됩니다.

Statistics and Machine Learning Toolbox™에서는 다음과 같이 카이제곱 분포를 사용하는 여러 방법을 제공합니다.

• 지정된 분포 모수를 이용해 분포 전용 함수(chi2cdf, chi2inv, chi2pdf, chi2rnd, chi2stat)를 사용합니다. 분포 전용 함수는 여러 카이제곱 분포의 모수를 받을 수 있습니다.

• 일반 분포 함수(cdf, icdf, pdf, random)를 지정된 분포 이름('Chisquare') 및 모수와 함께 사용합니다.

모수

카이제곱 분포는 다음 모수를 사용합니다.

모수	설명	지원
ν	자유도	ν = 1, 2, 3,...

자유도 모수는 일반적으로 정수이지만, 카이제곱 함수는 임의의 양수 값을 받습니다.

자유도 ν₁과 ν₂를 갖는 두 카이제곱 확률 변수의 합은 자유도가 ν = ν₁ + ν₂인 카이제곱 확률 변수입니다.

확률 밀도 함수

카이제곱 분포의 확률 밀도 함수(pdf)는 다음과 같습니다.

$$y=f\left(x|\nu \right)=\frac{x^{\left(\nu -2\right)/2}{e}^{-x/2}}{2^{\frac{\nu }{2}}\Gamma \left(\nu /2\right)},$$

이는 x > 0인 경우에 적용되며, 여기서 ν는 자유도이고 Γ( · )는 감마 함수입니다.

예제는 카이제곱 분포 pdf 계산하기 항목을 참조하십시오.

누적 분포 함수

카이제곱 분포의 누적 분포 함수(cdf)는 다음과 같습니다.

$$p=F(x|\nu )={\displaystyle {\int }_0^x\frac{t^{(\nu -2)/2}{e}^{-t/2}}{2^{\nu /2}\Gamma (\nu /2)}dt},$$

이는 x ≥ 0인 경우에 적용되며, 여기서 ν는 자유도이고 Γ( · )는 감마 함수입니다. 결과 p는 자유도가 ν인 카이제곱 분포에서 단일 관측값이 구간 [0, x]에 속할 확률입니다.

예제는 카이제곱 분포 cdf 계산하기 항목을 참조하십시오.

역누적 분포 함수

카이제곱 분포의 역누적 분포 함수(icdf)는 다음과 같습니다.

$$x=F^{-1}(p|\nu )=\{x:F(x|\nu )=p\},$$

여기서

$$p=F(x|\nu )={\displaystyle {\int }_0^x\frac{t^{(\nu -2)/2}{e}^{-t/2}}{2^{\nu /2}\Gamma (\nu /2)}}dt,$$

ν는 자유도이고 Γ( · )는 감마 함수입니다. 결과 p는 자유도가 ν인 카이제곱 분포에서 단일 관측값이 구간 [0, x]에 속할 확률입니다.

기술 통계량

카이제곱 분포의 평균은 ν입니다.

카이제곱 분포의 분산은 2ν입니다.

예제

카이제곱 분포 pdf 계산하기

자유도가 4인 카이제곱 분포의 pdf를 계산합니다.

x = 0:0.2:15;
y = chi2pdf(x,4);

pdf를 플로팅합니다.

figure;
plot(x,y)
xlabel('Observation')
ylabel('Probability Density')

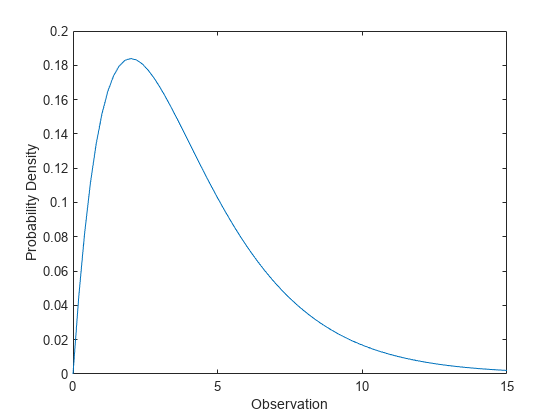
카이제곱 분포는 특히 자유도가 적은 경우 오른쪽 꼬리가 더 깁니다.

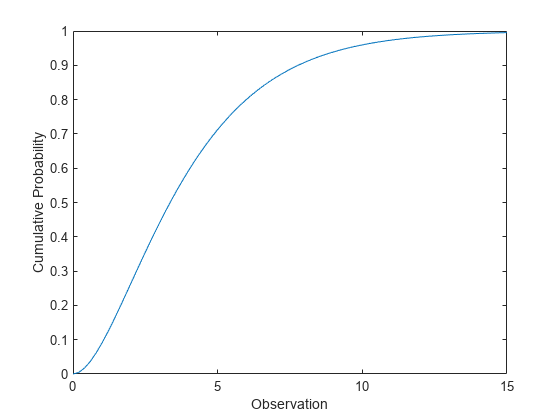
카이제곱 분포 cdf 계산하기

자유도가 4인 카이제곱 분포의 cdf를 계산합니다.

x = 0:0.2:15;
y = chi2cdf(x,4);

cdf를 플로팅합니다.

figure;
plot(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')

관련 분포

• F 분포 — F 분포는 모수 ν₁(분자 자유도)과 ν₂(분모 자유도)를 갖는 2-모수 분포입니다. F 분포는 $$F=\frac{\raisebox{1ex}{${\chi }_1^2$}\!\left/ \!\raisebox{-1ex}{${\nu }_1$}\right.}{\raisebox{1ex}{${\chi }_2^2$}\!\left/ \!\raisebox{-1ex}{${\nu }_2$}\right.}$$ 비율로 정의할 수 있습니다. 여기서 χ²₁과 χ²₂는 둘 다 독립적이며 각각 자유도가 ν₁과 ν₂인 카이제곱 분포입니다.

• 감마 분포 — 감마 분포는 모수 a(형태)와 b(스케일)를 갖는 2-모수 연속 분포입니다. 카이제곱 분포는 2a = ν 및 b = 2인 감마 분포와 같습니다.

• Noncentral Chi-Square Distribution — 비중심 카이제곱 분포는 모수 ν(자유도)와 δ(비중심성)를 갖는 2-모수 연속 분포입니다. 비중심 카이제곱 분포는 δ = 0인 경우 카이제곱 분포와 같습니다.

• 정규분포 — 정규분포는 모수 μ(평균)와 σ(표준편차)를 갖는 2-모수 연속 분포입니다. μ = 0이고 σ = 1이면 표준 정규분포가 발생합니다.

  Z₁, Z₂, …, Z_n이 독립적인 표준 정규 확률 변수이면 $${\displaystyle \sum _{i=1}^n{Z}_i{}^2}$$는 자유도가 ν = n – 1인 카이제곱 분포를 갖습니다.

  관측값이 n개인 하나의 세트가 분산 σ²과 표본 분산 s²으로 정규분포되어 있는 경우 $$\frac{\left(n-1\right)s^2}{{\sigma }^2}$$은 자유도가 ν = n – 1인 카이제곱 분포를 갖습니다. 이 관계는 함수 normfit에서 정규 모수 σ²의 추정값에 대한 신뢰구간을 계산하는 데 사용됩니다.

• 스튜던트 t 분포 — 스튜던트 t 분포는 모수 ν(자유도)를 갖는 1-모수 연속 분포입니다. Z가 표준 정규분포를 갖고 χ²이 자유도가 ν인 카이제곱 분포를 갖고 Z와 χ²이 독립적인 경우 $$\text{t = }\frac{Z}{\sqrt{{\chi }^2/\nu }}$$는 자유도가 ν인 스튜던트 t 분포를 갖습니다.

• Wishart Distribution — 위샤트 분포는 카이제곱 분포와 유사하되 차원이 더 높은 분포입니다.

참고 문헌

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.

[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.

참고 항목

chi2cdf | chi2pdf | chi2inv | chi2stat | chi2gof | chi2rnd

도움말 항목

• 확률 분포 사용하기
• 지원되는 분포