mldivide, \
x에 대한 선형 연립방정식 Ax = B의 해 구하기
설명
x = A\BA*x = B의 해를 구합니다. 행렬 A와 B의 행 개수는 동일해야 합니다. A가 준특이 행렬(badly scaled)이거나 유사 특이 행렬(Nearly Singular)이면 MATLAB®에서 경고 메시지가 표시되지만, 계산은 이에 관계없이 수행됩니다.
A가 스칼라인 경우A\B는A.\B와 동일합니다.A가 정사각n×n행렬이고B가n개 행을 갖는 행렬이면,x = A\B는 방정식A*x = B의 해가 존재하는 경우 그 해가 됩니다.A가m ~= n인 직사각m×n행렬이고B가m개 행을 갖는 행렬이면,A\B는 연립방정식A*x= B에 대한 최소제곱해(Least-squares Solution)를 반환합니다.x는 최소 노름 해가 아닐 수 있습니다.
예제
입력 인수
출력 인수
팁
연산자
/와\는 등식B/A = (A'\B')'의 관계에 있습니다.A가 정사각 행렬인 경우A\B는 대략적으로inv(A)*B와 같지만 MATLAB에서는A\B를 이와 다르게 더욱 견고한 방식으로 처리합니다.A의 랭크가A의 열 개수보다 작은 경우,x = A\B가 반드시 최소 노름 해가 되지는 않습니다.x =또는lsqminnorm(A,B)x =를 사용하여 최소 노름 최소제곱해를 계산할 수 있습니다.pinv(A)*B각기 다른 우변을 갖는 선형 시스템을 효율적으로 여러 번 풀려면
decomposition을 사용하십시오.decomposition객체를 사용하면 계수 행렬 분해를 여러 번 수행할 필요가 없으므로, 반복적으로 해를 구해야 하는 문제를 풀 때 적합합니다.
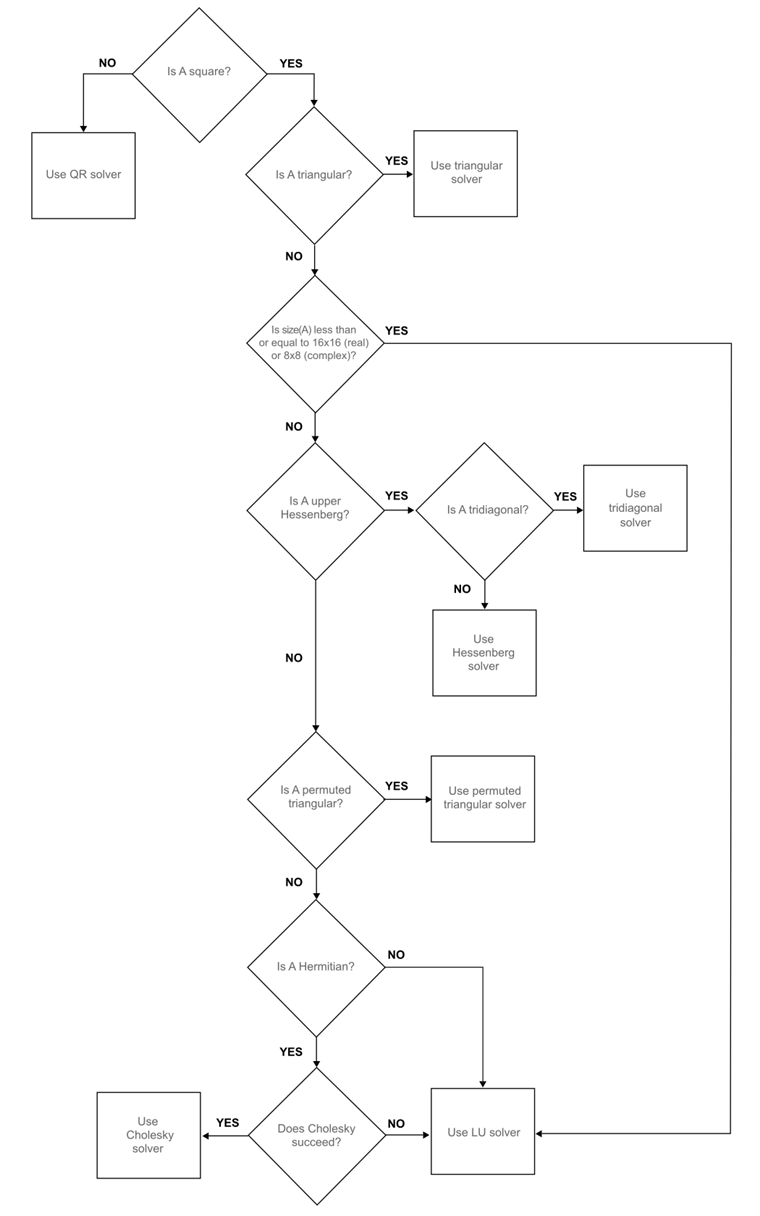
알고리즘
참고 문헌
[1] Gilbert, John R., and Tim Peierls. “Sparse Partial Pivoting in Time Proportional to Arithmetic Operations.” SIAM Journal on Scientific and Statistical Computing 9, no. 5 (September 1988): 862–874. https://doi.org/10.1137/0909058.
[2] Anderson, E., ed. LAPACK Users’ Guide. 3rd ed. Software, Environments, Tools. Philadelphia: Society for Industrial and Applied Mathematics, 1999. https://doi.org/10.1137/1.9780898719604.
[3] Davis, Timothy A. "Algorithm 832: UMFPACK V4.3 – an unsymmetric-pattern multifrontal method." ACM Transactions on Mathematical Software 30, no. 2 (June 2004): 196–199. https://doi.org/10.1145/992200.992206.
[4] Duff, Iain S. “MA57---a Code for the Solution of Sparse Symmetric Definite and Indefinite Systems.” ACM Transactions on Mathematical Software 30, no. 2 (June 2004): 118–144. https://doi.org/10.1145/992200.992202.
[5] Davis, Timothy A., John R. Gilbert, Stefan I. Larimore, and Esmond G. Ng. “Algorithm 836: COLAMD, a Column Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 377–380. https://doi.org/10.1145/1024074.1024080.
[6] Amestoy, Patrick R., Timothy A. Davis, and Iain S. Duff. “Algorithm 837: AMD, an Approximate Minimum Degree Ordering Algorithm.” ACM Transactions on Mathematical Software 30, no. 3 (September 2004): 381–388. https://doi.org/10.1145/1024074.1024081.
[7] Chen, Yanqing, Timothy A. Davis, William W. Hager, and Sivasankaran Rajamanickam. “Algorithm 887: CHOLMOD, Supernodal Sparse Cholesky Factorization and Update/Downdate.” ACM Transactions on Mathematical Software 35, no. 3 (October 2008): 1–14. https://doi.org/10.1145/1391989.1391995.
[8] Davis, Timothy A. “Algorithm 915, SuiteSparseQR: Multifrontal Multithreaded Rank-Revealing Sparse QR Factorization.” ACM Transactions on Mathematical Software 38, no. 1 (November 2011): 1–22. https://doi.org/10.1145/2049662.2049670.