stftLayer
Description
An STFT layer computes the short-time Fourier transform of the input. Use of this layer requires Deep Learning Toolbox™.
Creation
Description
layer = stftLayerstftLayer must be a real-valued dlarray (Deep Learning Toolbox) object in
"CBT" format with a size along the time dimension greater than the
length of Window. stftLayer formats the output as
"SCBT".
For more information, see Layer Output Format.
Note
When you initialize the learnable parameters of stftLayer, the
layer weights are set to the analysis window used to compute the transform. It is not
recommended to initialize the weights directly.
layer = stftLayer(PropertyName=Value)
Note
You cannot use this syntax to set the Weights
property.
Properties
STFT
This property is read-only.
Analysis window used to compute the STFT, specified as a vector with two or more elements.
Example: (1-cos(2*pi*(0:127)'/127))/2 and
hann(128)
Data Types: double | single
This property is read-only.
Number of overlapped samples, specified as a positive integer strictly smaller
than the length of Window.
The stride between consecutive windows is the difference between the window length and the number of overlapped samples.
Data Types: double | single
This property is read-only.
Number of frequency points used to compute the discrete Fourier transform, specified as a positive integer greater than or equal to the window length. If not specified, this argument defaults to the length of the window.
Data Types: double | single
Layer transform mode, specified as one of these:
"mag"— STFT magnitude"squaremag"— STFT squared magnitude"logmag"— Natural logarithm of the STFT magnitude"logsquaremag"— Natural logarithm of the STFT squared magnitude"realimag"— Real and imaginary parts of the STFT, concatenated along the channel dimension
Data Types: char | string
Layer
Layer weights, specified as [], a numeric array, or a
dlarray object.
The layer weights are learnable parameters.
You can use initialize (Deep Learning Toolbox)
to initialize the learnable parameters of a dlnetwork (Deep Learning Toolbox) that includes
stftLayer objects. When you initialize the layers,
initialize sets Weights to the analysis
window used to compute the transform. For more information, see Initialize Short-Time Fourier Transform Layer. (since R2025a)
It is not recommended to initialize the weights directly.
Data Types: double | single
Multiplier for weight learning rate, specified as a nonnegative scalar. If not
specified, this property defaults to zero, resulting in weights that do not update
with training. You can also set this property using the setLearnRateFactor (Deep Learning Toolbox) function.
Data Types: double | single
Layer name, specified as a character vector or a string scalar.
For Layer array input, the trainnet (Deep Learning Toolbox) and
dlnetwork (Deep Learning Toolbox) functions automatically assign
names to unnamed layers.
The stftLayer object stores this property as a character vector.
Data Types: char | string
This property is read-only.
Number of inputs to the layer, stored as 1. This layer accepts a
single input only.
Data Types: double
This property is read-only.
Input names, stored as {'in'}. This layer accepts a single input
only.
Data Types: cell
This property is read-only.
Number of outputs from the layer, stored as 1. This layer has a
single output only.
Data Types: double
This property is read-only.
Output names, stored as {'out'}. This layer has a single output
only.
Data Types: cell
Examples
Generate a signal sampled at 600 Hz for 2 seconds. The signal consists of a chirp with sinusoidally varying frequency content. Store the signal in a deep learning array with "CTB" format.
fs = 6e2;
x = vco(sin(2*pi*(0:1/fs:2)),[0.1 0.4]*fs,fs);
dlx = dlarray(x,"CTB");Create a short-time Fourier transform layer with default properties. Create a dlnetwork object consisting of a sequence input layer and the short-time Fourier transform layer. Specify a minimum sequence length of 128 samples. Run the signal through the predict method of the network.
ftl = stftLayer; dlnet = dlnetwork([sequenceInputLayer(1,MinLength=128) ftl]); netout = predict(dlnet,dlx);
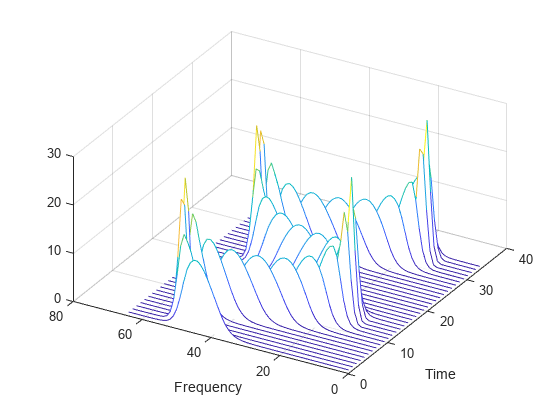
Convert the network output to a numeric array. Use the squeeze function to remove the length-1 channel and batch dimensions. Plot the magnitude of the STFT. The first dimension of the array corresponds to frequency and the second to time.
q = extractdata(netout); waterfall(squeeze(q)') set(gca,XDir="reverse",View=[30 45]) xlabel("Frequency") ylabel("Time")
Generate a 3 × 160 (× 1) array containing one batch of a three-channel, 160-sample sinusoidal signal. The normalized sinusoid frequencies are π/4 rad/sample, π/2 rad/sample, and 3π/4 rad/sample. Save the signal as a dlarray, specifying the dimensions in order. dlarray permutes the array dimensions to the "CBT" shape expected by a deep learning network.
nch = 3;
N = 160;
x = dlarray(cos(pi.*(1:nch)'/4*(0:N-1)),"CTB");Create a short-time Fourier transform layer that can be used with the sinusoid. Specify a 64-sample rectangular window, 48 samples of overlap between adjoining windows, and 1024 DFT points. By default, the layer outputs the magnitude of the STFT.
stfl = stftLayer(Window=rectwin(64), ... OverlapLength=48, ... FFTLength=1024);
Create a two-layer dlnetwork object containing a sequence input layer and the STFT layer you just created. Treat each channel of the sinusoid as a feature. Specify the signal length as the minimum sequence length for the input layer.
layers = [sequenceInputLayer(nch,MinLength=N) stfl]; dlnet = dlnetwork(layers);
Run the sinusoid through the forward method of the network.
dataout = forward(dlnet,x);
Convert the network output to a numeric array. Use the squeeze function to collapse the size-1 batch dimension. Permute the channel and time dimensions so that each array page contains a two-dimensional spectrogram. Plot the STFT magnitude separately for each channel in a waterfall plot.
q = squeeze(extractdata(dataout)); q = permute(q,[1 3 2]); for kj = 1:nch subplot(nch,1,kj) waterfall(q(:,:,kj)') view(30,45) zlabel("Ch. "+string(kj)) end

Since R2025a
Initialize short-time Fourier transform (STFT) layer weights to window, update deep learning neural network, and reset learnable parameters.
Define an array of seven layers: a sequence input layer, an STFT layer, a 2-D convolutional layer, a batch normalization layer, a rectified linear unit (ReLU) layer, a fully connected layer, and a softmax layer. There is one feature in the sequence input. Set the minimum signal length in the sequence input layer to 512 samples. For the STFT layer, use a 256-sample Hamming window and an overlap length of 128 samples.
win = hamming(256); layers = [ sequenceInputLayer(1,MinLength=512) stftLayer(Window=win,OverlapLength=128,Name="stft") convolution2dLayer(4,16,Padding="same") batchNormalizationLayer reluLayer fullyConnectedLayer(3) softmaxLayer];
Create a deep learning neural network from the layer array. By default, the dlnetwork function initializes the network at creation. For reproducibility, use the default random number generator.
rng("default")
net = dlnetwork(layers);Display the table of learnable parameters. The network weights and bias are nonempty dlarray objects.
tInit1 = net.Learnables
tInit1=7×3 table
Layer Parameter Value
___________ _________ ____________________
"stft" "Weights" {256×1 dlarray}
"conv" "Weights" { 4×4×1×16 dlarray}
"conv" "Bias" { 1×1×16 dlarray}
"batchnorm" "Offset" { 1×16 dlarray}
"batchnorm" "Scale" { 1×16 dlarray}
"fc" "Weights" { 3×2064 dlarray}
"fc" "Bias" { 3×1 dlarray}
Compare the initialized weights of the STFT layer from the list of learnable parameters with the Window property of the STFT layer. The stftLayer weights are single precision and initialized to the specified window.
isequal(tInit1.Value{1},single(net.Layers(2).Window))ans = logical
1
Set the learnable parameters to empty arrays.
net = dlupdate(@(x)[],net); net.Learnables
ans=7×3 table
Layer Parameter Value
___________ _________ ____________
"stft" "Weights" {0×0 double}
"conv" "Weights" {0×0 double}
"conv" "Bias" {0×0 double}
"batchnorm" "Offset" {0×0 double}
"batchnorm" "Scale" {0×0 double}
"fc" "Weights" {0×0 double}
"fc" "Bias" {0×0 double}
Reinitialize the network. Display the network and the learnable parameters. The network weights and bias are nonempty dlarray objects.
net = initialize(net); tInit2 = net.Learnables
tInit2=7×3 table
Layer Parameter Value
___________ _________ ____________________
"stft" "Weights" {256×1 dlarray}
"conv" "Weights" { 4×4×1×16 dlarray}
"conv" "Bias" { 1×1×16 dlarray}
"batchnorm" "Offset" { 1×16 dlarray}
"batchnorm" "Scale" { 1×16 dlarray}
"fc" "Weights" { 3×2064 dlarray}
"fc" "Bias" { 3×1 dlarray}
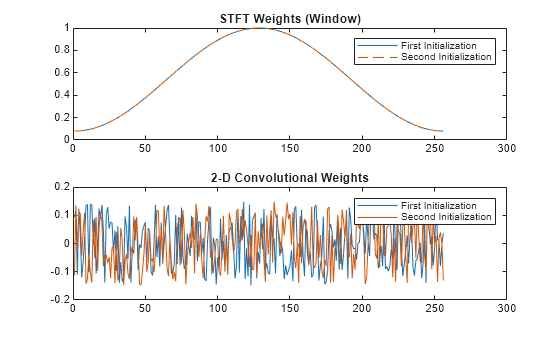
Compare the weights from the STFT and 2-D convolutional layers along the two initialization calls. The STFT layer sets the weights using the specified window, while the convolutional layer weights consists of a new set of random values.
tiledlayout flow nexttile plot(tInit1.Value{1}) hold on plot(tInit2.Value{1},"--") hold off title("STFT Weights (Window)") legend(["First" "Second"] + " Initialization") nexttile plot([tInit1.Value{2}(:) tInit2.Value{2}(:)]) title("2-D Convolutional Weights") legend(["First" "Second"] + " Initialization")
More About
The short-time Fourier transform (STFT) is used to analyze how the frequency content of a nonstationary signal changes over time. The magnitude squared of the STFT is known as the spectrogram time-frequency representation of the signal. For more information about the spectrogram and how to compute it using Signal Processing Toolbox™ functions, see Spectrogram Computation with Signal Processing Toolbox.
The STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. Most window functions taper off at the edges to avoid spectral ringing. The DFT of each windowed segment is added to a complex-valued matrix that contains the magnitude and phase for each point in time and frequency. The STFT matrix has
columns, where Nx is the length of the signal x(n) and the ⌊⌋ symbols denote the floor function. The number of rows in the matrix equals NDFT, the number of DFT points, for centered and two-sided transforms and an odd number close to NDFT/2 for one-sided transforms of real-valued signals.
The mth column of the STFT matrix contains the DFT of the windowed data centered about time mR:
stftLayer formats the output as "SCBT", a sequence
of 1-D images where the image height corresponds to frequency, the second dimension
corresponds to channel, the third dimension corresponds to batch, and the fourth dimension
corresponds to time.
You can feed the output of
stftLayerunchanged to a 1-D convolutional layer when you want to convolve along the frequency ("S") dimension. For more information, seeconvolution1dLayer(Deep Learning Toolbox).To feed the output of
stftLayerto a 1-D convolutional layer when you want to convolve along the time ("T") dimension, you must place a flatten layer after thestftLayer. For more information, seeflattenLayer(Deep Learning Toolbox).You can feed the output of
stftLayerunchanged to a 2-D convolutional layer when you want to convolve along the frequency ("S") and time ("T") dimensions. For more information, seeconvolution2dLayer(Deep Learning Toolbox).To use
stftLayeras part of a recurrent neural network, you must place a flatten layer after thestftLayer. For more information, seelstmLayer(Deep Learning Toolbox) andgruLayer(Deep Learning Toolbox).To use the output of
stftLayerwith a fully connected layer as part of a classification workflow, you must reduce the time ("T") dimension of the output so that it has size 1. To reduce the time dimension of the output, place a global pooling layer before the fully connected layer. For more information, seeglobalAveragePooling2dLayer(Deep Learning Toolbox) andfullyConnectedLayer(Deep Learning Toolbox).
Extended Capabilities
Usage notes and limitations:
You can generate generic C/C++ code that does not depend on third-party libraries and deploy the generated code to hardware platforms.
Usage notes and limitations:
You can generate CUDA code that is independent of deep learning libraries and deploy the generated code to platforms that use NVIDIA® GPU processors.
Version History
Introduced in R2021bStarting in R2025a, you can use initialize (Deep Learning Toolbox) to
initialize learnable parameters for deep learning neural networks that include
stftLayer objects.
Starting in R2025a, the default value of the Weights property is
[]. Prior to R2025a, stftLayer set the default value
to the analysis window used to compute the transform.
The stftLayer object supports:
C/C++ code generation. You must have MATLAB® Coder™ to generate C/C++ code.
Code generation for NVIDIA GPUs. You must have GPU Coder™ to generate GPU code.
Starting in R2023b, stftLayer initializes the
Weights learnable parameter to the analysis window used to compute
the transform. Previously, the parameter was initialized to an array containing the Gabor
atoms for the STFT.
The OutputMode property of stftLayer will be
removed in a future release. Update your code and networks to make them compatible with
stftLayer output in "SCBT" format. For more
information, see Layer Output Format.
See Also
Apps
- Deep Network Designer (Deep Learning Toolbox)
Objects
istftLayer|dlarray(Deep Learning Toolbox) |dlnetwork(Deep Learning Toolbox)
Functions
dlstft|stft|dlistft|istft|stftmag2sig
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)