istft
Inverse short-time Fourier transform
Description
x = istft(s)s.
x = istft(___,Name,Value)
Examples
Generate a three-channel signal consisting of three different chirps sampled at 1 kHz for 1 second.
The first channel consists of a concave quadratic chirp with instantaneous frequency 100 Hz at t = 0 and crosses 300 Hz at t = 1 second. It has an initial phase equal to 45 degrees.
The second channel consists of a convex quadratic chirp with instantaneous frequency 200 Hz at t = 0 and crosses 600 Hz at t = 1 second.
The third channel consists of a logarithmic chirp with instantaneous frequency 300 Hz at t = 0 and crosses 500 Hz at t = 1 second.
Compute the STFT of the multichannel signal using a periodic Hamming window of length 256 and an overlap length of 15 samples.
fs = 1e3; t = 0:1/fs:1-1/fs; x = [chirp(t,100,1,300,"quadratic",45,"concave"); chirp(t,200,1,600,"quadratic",[],"convex"); chirp(t,300,1,500,"logarithmic")]'; [S,F,T] = stft(x,fs,Window=hamming(256,"periodic"),OverlapLength=15);
Plot the original and reconstructed versions of the first and second channels.
[ix,ti] = istft(S,fs,Window=hamming(256,"periodic"),OverlapLength=15); plot(t,x(:,1)',LineWidth=1.5) hold on plot(ti,ix(:,1)',"r--") hold off legend(["Original Channel 1" "Reconstructed Channel 1"])

plot(t,x(:,2)',LineWidth=1.5) hold on plot(ti,ix(:,2)',"r--") legend(["Original Channel 2" "Reconstructed Channel 2"])

The phase vocoder performs time stretching and pitch scaling by transforming the audio in the frequency domain. This diagram shows the operations involved in the phase vocoder implementation.

The phase vocoder takes the STFT of a signal with an analysis window of hop size and then performs an ISTFT with a synthesis window of hop size . The vocoder thus takes advantage of the WOLA method. To time stretch a signal, the analysis window uses a larger number of overlap samples than the synthesis. As a result, there are more samples at the output than at the input (), although the frequency content remains the same. Now, you can pitch scale this signal by playing it back at a higher sample rate, which produces a signal with the original duration but a higher pitch.
Load an audio file containing a fragment of Handel's "Hallelujah Chorus" sampled at 8192 Hz.
load handelDesign a root-Hann window of length 512.
wlen = 512;
win = sqrt(hann(wlen,"periodic"));Implement the phase vocoder by using an analysis window of overlap 192 and a synthesis window of overlap 166.
If the analysis and synthesis windows are the same but the overlap length is changed, there is an additional gain/loss that you must adjust. This is a common approach to implementing a phase vocoder.
In this example, the analysis and synthesis hop sizes are close enough that it is not necessary to compensate for phase shift.
noverlapA = 192;
noverlapS = 166;
S = stft(y,Fs,Window=win,OverlapLength=noverlapA);
iy = istft(S,Fs,Window=win,OverlapLength=noverlapS);
% To hear, type soundsc(y,Fs), pause(10), soundsc(iy,Fs)Calculate the hop ratio and use it to adjust the gain of the reconstructed signal. Use the hop ratio to calculate the frequency of the pitch-shifted data.
hopRatio = (wlen-noverlapS)/(wlen-noverlapA);
iyg = iy*hopRatio;
Fp = Fs*hopRatio;
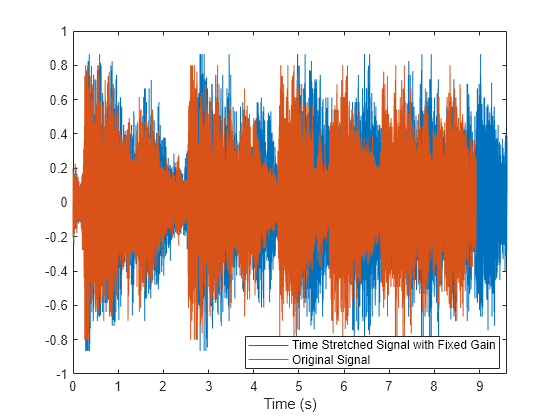
% To hear, type soundsc(iyg,Fs), pause(15), soundsc(iyg,Fp)Plot the original signal and the time-stretched signal with fixed gain.
plot((0:length(iyg)-1)/Fs,iyg,(0:length(y)-1)/Fs,y) xlabel("Time (s)") xlim([0 (length(iyg)-1)/Fs]) legend(["Time Stretched Signal with Fixed Gain" "Original Signal"], ... Location="best")
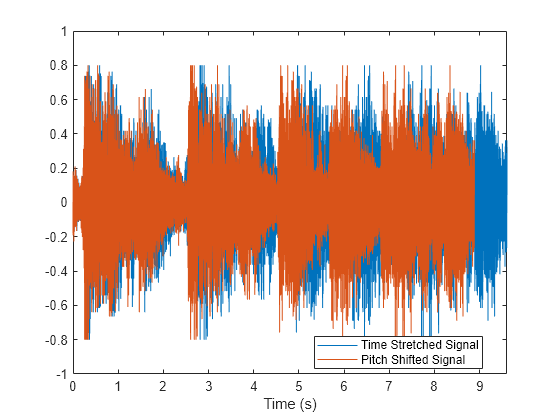
Compare the time-stretched signal and the pitch-shifted signal on the same plot.
plot((0:length(iy)-1)/Fs,iy,(0:length(iy)-1)/Fp,iy) xlabel("Time (s)") xlim([0 (length(iyg)-1)/Fs]) legend(["Time Stretched Signal" "Pitch Shifted Signal"], ... Location="best")
To better understand the effect of pitch shifting data, consider a 10 Hz sinusoid sampled at Fs for 2 seconds.
t = 0:1/Fs:2; x = sin(2*pi*10*t);
Calculate the short-time Fourier transform and the inverse short-time Fourier transform with overlap lengths 192 and 166, respectively.
Sx = stft(x,Fs,Window=win,OverlapLength=noverlapA); ix = istft(Sx,Fs,Window=win,OverlapLength=noverlapS);
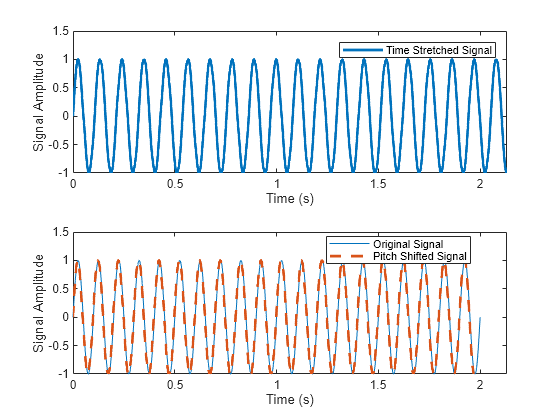
Plot the original signal on one plot and the time-stretched and pitch shifted signal on another.
tiledlayout(2,1) nexttile plot((0:length(ix)-1)/Fs,ix,LineWidth=2) xlabel("Time (s)") ylabel("Signal Amplitude") xlim([0 (length(ix)-1)/Fs]) legend("Time Stretched Signal") nexttile plot((0:length(x)-1)/Fs,x) hold on plot((0:length(ix)-1)/Fp,ix,"--",LineWidth=2) legend(["Original Signal" "Pitch Shifted Signal"], ... Location="best") hold off xlabel("Time (s)") ylabel("Signal Amplitude") xlim([0 (length(ix)-1)/Fs])
Generate a complex sinusoid of frequency 1 kHz and duration 2 seconds.
fs = 1e3; ts = 0:1/fs:2-1/fs; x = exp(2j*pi*100*cos(2*pi*2*ts));
Design a periodic Hann window of length 100 and set the number of overlap samples to 75. Check the window and overlap length for COLA compliance.
nwin = 100;
win = hann(nwin,"periodic");
nOverlap = 75;
tf = iscola(win,nOverlap)tf = logical
1
Zero-pad the signal to remove edge-effects. To avoid truncation, pad the input signal with zeros such that
is an integer. Set the FFT length to 128. Compute the short-time Fourier transform of the complex signal.
nPad = 100;
xZero = [zeros(1,nPad) x zeros(1,nPad)];
fftL = 128;
s = stft(xZero,fs,Window=win, ...
OverlapLength=nOverlap,FFTLength=fftL);Calculate the inverse short-time Fourier transform and remove the zeros for perfect reconstruction.
[is,ti] = istft(s,fs,Window=win, ...
OverlapLength=nOverlap,FFTLength=fftL);
is(1:nPad) = [];
is(end-nPad+1:end) = [];
ti = ti(1:end-2*nPad);Plot the real parts of the original and reconstructed signals. The imaginary part of the signal is also reconstructed perfectly.
plot(ts,real(x)) hold on plot(ti,real(is),"--") xlim([0 0.5]) xlabel("Time (s)") ylabel("Amplitude (V)") legend("Original Signal","Reconstructed Signal") hold off

Generate a sinusoid sampled at 2 kHz for 1 second.
fs = 2e3; t = 0:1/fs:1-1/fs; x = 5*sin(2*pi*10*t);
Design a periodic Hamming window of length 120. Check the COLA constraint for the window with an overlap of 80 samples. The window-overlap combination is COLA compliant.
win = hamming(120,"periodic");
nOverlap = 80;
tf = iscola(win,nOverlap)tf = logical
1
Set the FFT length to 512. Compute the short-time Fourier transform.
fftL = 512; s = stft(x,fs,Window=win,OverlapLength=nOverlap,FFTLength=fftL);
Calculate the inverse short-time Fourier transform.
[X,T] = istft(s,fs,Window=win,OverlapLength=nOverlap,FFTLength=fftL, ... Method="ola",ConjugateSymmetric=true);
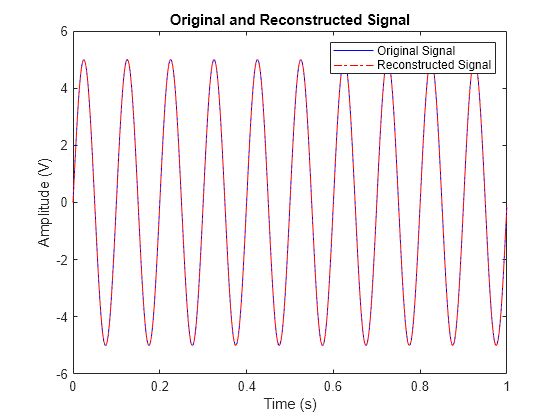
Plot the original and reconstructed signals.
plot(t,x,"b") hold on plot(T,X,"-.r") xlabel("Time (s)") ylabel("Amplitude (V)") title("Original and Reconstructed Signal") legend("Original Signal","Reconstructed Signal") hold off
Input Arguments
Short-time Fourier transform, specified as a matrix or a 3-D array. For
single-channel signals, specify s as a matrix with time increasing
across the columns and frequency increasing down the rows. For multichannel signals,
specify s as a 3-D array with the third dimension corresponding to
the channels. The frequency and time vectors are obtained as outputs of stft.
Note
If you want x and s to be the same
length, the value of
(length(
must be an integer. Use x)-noverlap)/(length(window)-noverlap)Window to
specify the length of window and OverlapLength to specify noverlap.
Data Types: double | single
Complex Number Support: Yes
Sample rate in hertz, specified as a positive scalar.
Data Types: double | single
Sample time, specified as a duration scalar.
Example: seconds(1) is a
duration
Data Types: duration
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: istft(s,Window=win,OverlapLength=50,FFTLength=128) windows
the data using the window win, with 50 samples overlap between adjoining
segments and 128 DFT points.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: istft(s,'Window',win,'OverlapLength',50,'FFTLength',128)
windows the data using the window win, with 50 samples overlap between
adjoining segments and 128 DFT points.
Windowing function, specified as a vector. If you do not specify the window or
specify it as empty, the function uses a periodic Hann window of length 128. The
length of Window must be greater than or equal to 2.
For a list of available windows, see Windows.
Example: hann(N+1) and
(1-cos(2*pi*(0:N)'/N))/2 both specify a Hann window of length
N + 1.
Data Types: double | single
Number of overlapped samples, specified as a nonnegative integer smaller than the
length of window. If you omit OverlapLength or
specify it as empty, it is set to the largest integer less than 75% of the window
length, which turns out to be 96 samples for the default Hann window.
Data Types: double | single
Number of DFT points, specified as a positive integer greater than or equal to the
length of the window. To achieve perfect time-domain reconstruction, you must set the
number of DFT points to match that used in stft.
Data Types: double | single
Method of overlap-add, specified as one of these:
"wola"— Weighted overlap-add"ola"— Overlap-add
Conjugate symmetry of the original signal, specified as true or
false. If this option is set to true,
istft assumes that the input s is
symmetric, otherwise no symmetric assumption is made. When s is
not exactly conjugate symmetric due to round-off error, setting the name-value pair to
true ensures that the STFT is treated as if it were conjugate
symmetric. If s is conjugate symmetric, then the inverse
transform computation is faster, and the output is real.
STFT frequency range, specified as "centered",
"twosided", or "onesided".
"centered"— Treatsas a two-sided, centered STFT. Ifnfftis even, thensis considered to be computed over the interval (–π, π] rad/sample. Ifnfftis odd, thensis considered to be computed over the interval (–π, π) rad/sample. If you specify time information, then the intervals are (–fs, fs/2] cycles/unit time and (–fs, fs/2) cycles/unit time, respectively, where fs is the sample rate."twosided"— Treatsas a two-sided STFT computed over the interval [0, 2π) rad/sample. If you specify time information, then the interval is [0, fs) cycles/unit time."onesided"— Treatsas a one-sided STFT. Ifnfftis even, thensis considered to be computed over the interval [0, π] rad/sample. Ifnfftis odd, thensis considered to be computed over the interval [0, π) rad/sample. If you specify time information, then the intervals are [0, fs/2] cycles/unit time and [0, fs/2) cycles/unit time, respectively, where fs is the sample rate.Note
When this argument is set to
"onesided",istftassumes the values in the positive Nyquist range were computed without conserving the total power.
For an example, see STFT Frequency Ranges.
Data Types: char | string
Input time dimension, specified as "acrosscolumns" or
"downrows".
"downrows"—istftassumes that the time dimension ofsis down the rows and the frequency dimension is across the columns."acrosscolumns"—istftassumes that the time dimension ofsis across the columns and the frequency dimension is down the rows.
Output Arguments
Reconstructed signal in the time domain, returned as a vector or a matrix.
Data Types: single | double
Time instants, returned as a vector.
Data Types: double | single
More About
To compute the inverse short-time Fourier transform, take the IFFT of each DFT vector of the STFT and overlap-add the inverted signals.
Recall that the STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. The ISTFT is calculated as follows.
where is the DFT of the windowed data centered about time and . The inverse STFT is a perfect reconstruction of the original signal as long as where is a nonzero constant and equals 0 or 1. For more information, see Constant Overlap-Add (COLA) Constraint. This figure depicts the steps in reconstructing the original signal.
To ensure successful reconstruction of nonmodified spectra, the analysis window must satisfy the COLA constraint. In general, if the analysis window satisfies the condition where is a nonzero constant and equals 0 or 1, the window is considered to be COLA-compliant. Additionally, COLA compliance can be described as either weak or strong.
Weak COLA compliance implies that the Fourier transform of the analysis window has zeros at frame-rate harmonics such that
Alias cancellation is disturbed by spectral modifications. Weak COLA relies on alias cancellation in the frequency domain. Therefore, perfect reconstruction is possible using weakly COLA-compliant windows as long as the signal has not undergone any spectral modifications.
For strong COLA compliance, the Fourier transform of the window must be bandlimited consistently with downsampling by the frame rate such that
This equation shows that no aliasing is allowed by the strong COLA constraint. Additionally, for strong COLA compliance, the value of the constant must equal 1. In general, if the short-time spectrum is modified in any way, a stronger COLA compliant window is preferred.
You can use the iscola function to check for weak COLA compliance. The number of summations used to check COLA compliance is dictated by the window length and hop size. In general, it is common to use in for weighted overlap-add (WOLA), and for overlap-add (OLA). By default, istft uses the WOLA method, by applying a synthesis window before performing the overlap-add method.
In general, the synthesis window is the same as the analysis window. You can construct useful WOLA windows by taking the square root of a strong OLA window. You can use this method for all nonnegative OLA windows. For example, the root-Hann window is a good example of a WOLA window.
In general, computing the STFT of an input signal and inverting it does not result in perfect reconstruction. If you want the output of ISTFT to match the original input signal as closely as possible, the signal and the window must satisfy the following conditions:
Input size — If you invert the output of
stftusingistftand want the result to be the same length as the input signalx, the value ofmust be an integer. In the equation, Nx is the length of the signal, M is the length of the window, and L is the overlap length.
COLA compliance — Use COLA-compliant windows, assuming that you have not modified the short-time Fourier transform of the signal.
Padding — If the length of the input signal is such that the value of k is not an integer, zero-pad the signal before computing the short-time Fourier transform. Remove the extra zeros after inverting the signal.
You can use the stftmag2sig
function to obtain an estimate of a signal reconstructed from the magnitude of its
STFT.
References
[1] Crochiere, R. E. "A Weighted Overlap-Add Method of Short-Time Fourier Analysis/Synthesis." IEEE Transactions on Acoustics, Speech and Signal Processing. Vol. 28, Number 1, Feb. 1980, pp. 99–102.
[2] Gotzen, A. D., N. Bernardini, and D. Arfib. "Traditional Implementations of a Phase-Vocoder: The Tricks of the Trade." Proceedings of the COST G-6 Conference on Digital Audio Effects (DAFX-00), Verona, Italy, Dec 7–9, 2000.
[3] Griffin, Daniel W., and Jae S. Lim. "Signal Estimation from Modified Short-Time Fourier Transform." IEEE Transactions on Acoustics, Speech and Signal Processing. Vol. 32, Number 2, April 1984, pp. 236–243.
[4] Laroche, Jean, and Mark Dolson. "Improved Phase Vocoder Time-Scale Modification of Audio." IEEE Transactions on Speech and Audio Processing 7, no. 3 (May 1999): 323–32. https://doi.org/10.1109/89.759041.
[5] Portnoff, M. R. "Time-Frequency Representation of Digital Signals and Systems Based on Short-Time Fourier analysis." IEEE Transactions on Acoustics, Speech and Signal Processing. Vol. 28, Number 1, Feb 1980, pp. 55–69.
[6] Smith, Julius Orion. Spectral Audio Signal Processing. https://ccrma.stanford.edu/~jos/sasp/, online book, 2011 edition, accessed Nov. 2018.
[7] Sharpe, Bruce. Invertibility of Overlap-Add Processing. https://gauss256.github.io/blog/cola.html, accessed July 2019.
Extended Capabilities
The
istft function supports tall arrays with the following usage
notes and limitations:
InputTimeDimension must be always specified and set to
"downrows".
For more information, see Tall Arrays.
Usage notes and limitations:
The ConjugateSymmetric argument is not supported for code
generation.
Usage notes and limitations:
The ConjugateSymmetric argument is not supported for code
generation.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The istft function
supports GPU array input with these usage notes and limitations:
Unless ConjugateSymmetric is set to true, the
output x is always complex even if all the imaginary parts are
zero.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2019a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)