wavedec2
멀티레벨 2차원 이산 웨이블릿 변환
설명
[은 웨이블릿 C,S] = wavedec2(X,N,wname)wname을 사용하여 레벨 N에서 행렬 X의 웨이블릿 분해를 반환합니다. 출력 분해 구조체는 웨이블릿 분해 벡터 C와 레벨 및 방향 계수 개수를 포함하는 북키핑(bookkeeping) 행렬 S로 구성됩니다.
참고
gpuArray 입력값을 지원하는 모드는 "symh"("sym") 및 "per"입니다. 입력값이 gpuArray인 경우 현재 확장 모드가 "per"이 아니면 wavedec2에 사용되는 이산 웨이블릿 변환 확장 모드는 기본적으로 "symh"로 설정됩니다. GPU에서 멀티레벨 2차원 이산 웨이블릿 변환 예제를 참조하십시오.
예제
이 예제에서는 웨이블릿 분해 레벨 세부성분의 영상을 추출 및 표시하는 방법을 보여줍니다.
영상을 불러옵니다. haar 웨이블릿을 사용하여 영상의 레벨 2 웨이블릿 분해를 수행합니다.
load belmont1 [c,s]=wavedec2(X,2,"haar");
레벨 1 근사 계수와 세부성분 계수를 추출합니다.
[H1,V1,D1] = detcoef2("all",c,s,1); A1 = appcoef2(c,s,"haar",1);
wcodemat를 사용하여 해당 절댓값을 기반으로 계수를 다시 스케일링합니다. 다시 스케일링한 계수를 표시합니다.
V1img = wcodemat(V1,255,"mat",1); H1img = wcodemat(H1,255,"mat",1); D1img = wcodemat(D1,255,"mat",1); A1img = wcodemat(A1,255,"mat",1); tiledlayout(2,2) nexttile imagesc(A1img) colormap pink(255) title("Approximation Coef. of Level 1") nexttile imagesc(H1img) title("Horizontal Detail Coef. of Level 1") nexttile imagesc(V1img) title("Vertical Detail Coef. of Level 1") nexttile imagesc(D1img) title("Diagonal Detail Coef. of Level 1")
레벨 2 근사 계수와 세부성분 계수를 추출합니다.
[H2,V2,D2] = detcoef2("all",c,s,2); A2 = appcoef2(c,s,"haar",2);
wcodemat를 사용하여 해당 절댓값을 기반으로 계수를 다시 스케일링합니다. 다시 스케일링한 계수를 표시합니다.
V2img = wcodemat(V2,255,"mat",1); H2img = wcodemat(H2,255,"mat",1); D2img = wcodemat(D2,255,"mat",1); A2img = wcodemat(A2,255,"mat",1); figure tiledlayout(2,2) nexttile imagesc(A2img) colormap pink(255) title("Approximation Coef. of Level 2") nexttile imagesc(H2img) title("Horizontal Detail Coef. of Level 2") nexttile imagesc(V2img) title("Vertical Detail Coef. of Level 2") nexttile imagesc(D2img) title("Diagonal Detail Coef. of Level 2")
이 예제에서는 wavedec2 출력 행렬의 구조체를 보여줍니다.
영상을 불러와서 표시합니다.
load mask
imagesc(X)
colormap(map)
현재 이산 웨이블릿 변환 확장 모드를 저장합니다.
origMode = dwtmode("status","nodisplay");
주기적 경계 처리로 변경합니다. dwtmode 함수는 DWT 확장 모드가 변경되고 있음을 나타내는 메시지를 표시합니다.
dwtmode("per")
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
! WARNING: Change DWT Extension Mode !
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
*****************************************
** DWT Extension Mode: Periodization **
*****************************************
db1(Haar) 웨이블릿을 사용하여 영상의 레벨 3 분해를 수행합니다.
[c,s] = wavedec2(X,3,"db1");영상 X 및 계수 벡터 c의 요소 개수를 반환합니다. 각각의 요소 개수가 같은지 확인합니다.
numel(X)
ans = 65536
numel(c)
ans = 65536
북키핑 행렬 s를 표시합니다. 첫 번째 행은 영상의 성긴 스케일 근사의 크기를 표시합니다. 마지막 행은 원본 영상의 크기를 표시합니다. 중간 행은 성긴 스케일에서 세밀한 스케일로 진행하면서 세 레벨의 분해에서의 세부성분 계수의 차원을 표시합니다.
s
s = 5×2
32 32
32 32
64 64
128 128
256 256
이산 웨이블릿 변환 확장 모드를 원래 모드로 초기화합니다.
dwtmode(origMode,"nodisplay")지원되는 GPU를 보려면 GPU 연산 요구 사항 (Parallel Computing Toolbox) 항목을 참조하십시오.
영상을 불러옵니다. gpuArray를 사용하여 GPU에 영상을 놓습니다. 현재 확장 모드를 저장합니다.
load mask imgg = gpuArray(X); origMode = dwtmode("status","nodisp");
dwtmode를 사용하여 확장 모드를 0 채우기로 변경합니다. db4 웨이블릿을 사용하여 GPU에서 영상의 3-레벨 DWT를 구합니다.
dwtmode("zpd","nodisp") [c,s] = wavedec2(imgg,3,"db4");
현재 확장 모드 "zpd"는 gpuArray 입력값에서 지원되지 않습니다. 따라서 DWT는 대신 "sym" 확장 모드를 사용하여 수행됩니다. 이를 확인하기 위해 확장 모드를 "sym"으로 설정하고 noisdoppg에 DWT를 수행한 다음 이전 결과와 비교합니다.
dwtmode("sym","nodisp") [csym,ssym] = wavedec2(imgg,3,"db4"); [max(abs(c-csym)) max(abs(s-ssym))]
ans =
0 0 0
현재 확장 모드를 "per"로 설정하고 imgg의 3-레벨 DWT를 구합니다. 확장 모드 "per"은 gpuArray 입력값에서 지원됩니다. 결과가 "sym" 결과와 다른지 확인합니다.
dwtmode("per","nodisp") [cper,sper] = wavedec2(imgg,3,"db4"); [length(csym) ; length(cper)]
ans = 2×1
71542
65536
ssym
ssym = 5×2
38 38
38 38
69 69
131 131
256 256
sper
sper = 5×2
32 32
32 32
64 64
128 128
256 256
확장 모드를 원래 설정으로 복원합니다.
dwtmode(origMode,"nodisp")입력 인수
출력 인수
웨이블릿 분해 벡터입니다. 벡터 C는 레벨별로 정렬된 근사 계수 및 세부성분 계수를 포함합니다. 북키핑 행렬 S는 C를 구문 분석하는 데 사용됩니다.
벡터 C는 A(N), H(N), V(N), D(N), H(N-1), V(N-1), D(N-1), …, H(1), V(1), D(1)로 구성됩니다. 여기서 A, H, V 및 D는 각각 행 벡터입니다. 각 벡터는 행렬의 열별 저장소입니다.
A는 근사 계수를 포함합니다.
H는 가로 세부성분 계수를 포함합니다.
V는 세로 세부성분 계수를 포함합니다.
D는 대각 세부성분 계수를 포함합니다.
데이터형: double
북키핑 행렬입니다. 행렬 S는 레벨별 웨이블릿 계수의 차원을 포함하며 웨이블릿 분해 벡터 C를 구문 분석하는 데 사용됩니다.
S(1,:)= 근사 계수의 크기(N).S(i,:)=i= 2, ...N+1및S(N+2,:) = size(X)에 대한 세부성분 계수의 크기(N-i+2).
다음 도식은 512×512 행렬의 웨이블릿 분해에서 C와 S 사이의 관계를 보여줍니다.
X가 인덱스 영상을 나타내는 경우, 출력값 배열 cA, cH, cV 및 cD는 m×n 행렬입니다. X가 트루컬러 영상을 나타내는 경우, 이는 m×n×3 배열입니다. 여기서 각 m×n 행렬은 세 번째 차원을 따라 빨간색, 녹색 또는 파란색 평면을 나타냅니다. 벡터 C의 크기 및 행렬 S의 크기는 분석되는 영상의 유형에 따라 달라집니다.
트루컬러 영상의 경우, 분해 벡터 C 및 그에 대응하는 북키핑 행렬 S는 여기에 보이는 것과 같이 표시될 수 있습니다.
알고리즘
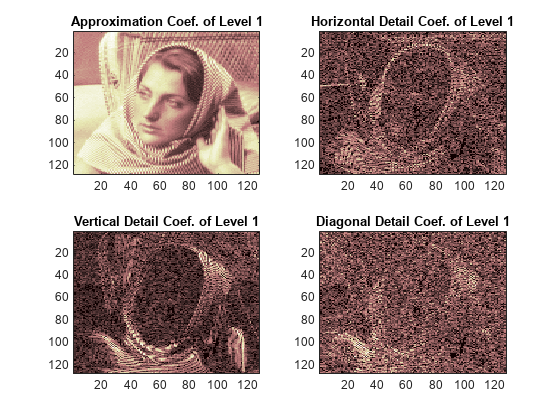
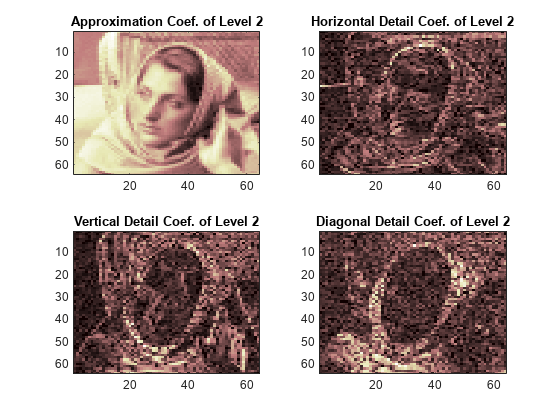
영상의 경우, 2차원 웨이블릿 및 텐서 곱에 의해 1차원 벡터에서 구한 스케일링 함수에 1차원의 경우와 유사한 알고리즘을 사용할 수 있습니다. 이 종류의 2차원 DWT는 레벨 j에서 근사 계수를 네 가지 성분으로 분해합니다. 즉 레벨 j+1에서의 근사, 세 방향(가로, 세로 및 대각선)의 세부성분으로 분해합니다.
다음 차트는 영상에 대한 기본적인 분해 단계를 설명합니다.
여기서
— 열 다운샘플링: 짝수 인덱스 열을 유지합니다.
— 행 다운샘플링: 짝수 인덱스 행을 유지합니다.
— 필터 X로 항목의 행을 컨벌루션합니다.
— 필터 X로 항목의 열을 컨벌루션합니다.
및
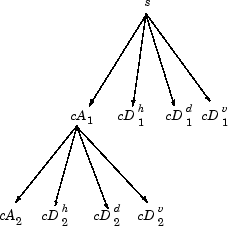
초기화: cA0 = s.
그러므로 J = 2의 경우, 2차원 웨이블릿 트리는 다음과 같은 형태임
참고 문헌
[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.
확장 기능
버전 내역
R2006a 이전에 개발됨
