kfoldMargin
Classification margins for cross-validated kernel classification model
Description
margin = kfoldMargin(CVMdl)ClassificationPartitionedKernel) CVMdl. For every fold,
kfoldMargin computes the classification margins for validation-fold
observations using a model trained on training-fold observations.
Examples
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, which are labeled as either bad ('b') or good ('g').
load ionosphereCross-validate a binary kernel classification model using the data.
CVMdl = fitckernel(X,Y,'Crossval','on')
CVMdl =
ClassificationPartitionedKernel
CrossValidatedModel: 'Kernel'
ResponseName: 'Y'
NumObservations: 351
KFold: 10
Partition: [1×1 cvpartition]
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
Properties, Methods
CVMdl is a ClassificationPartitionedKernel model. By default, the software implements 10-fold cross-validation. To specify a different number of folds, use the 'KFold' name-value pair argument instead of 'Crossval'.
Estimate the classification margins for validation-fold observations.
m = kfoldMargin(CVMdl); size(m)
ans = 1×2
351 1
m is a 351-by-1 vector. m(j) is the classification margin for observation j.
Plot the k-fold margins using a box plot.
boxplot(m,'Labels','All Observations') title('Distribution of Margins')
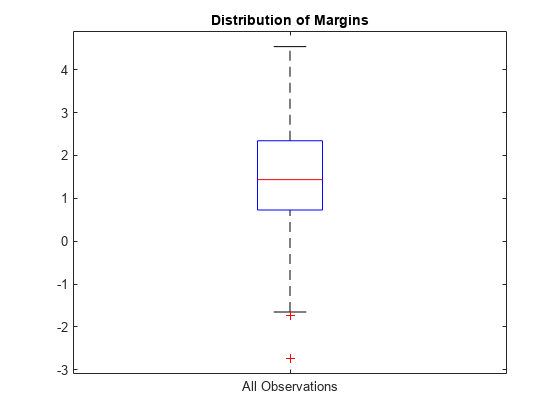
Perform feature selection by comparing k-fold margins from multiple models. Based solely on this criterion, the classifier with the greatest margins is the best classifier.
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, which are labeled either bad ('b') or good ('g').
load ionosphereRandomly choose 10% of the predictor variables.
rng(1); % For reproducibility p = size(X,2); % Number of predictors idxPart = randsample(p,ceil(0.1*p));
Cross-validate two binary kernel classification models: one that uses all of the predictors, and one that uses 10% of the predictors.
CVMdl = fitckernel(X,Y,'CrossVal','on'); PCVMdl = fitckernel(X(:,idxPart),Y,'CrossVal','on');
CVMdl and PCVMdl are ClassificationPartitionedKernel models. By default, the software implements 10-fold cross-validation. To specify a different number of folds, use the 'KFold' name-value pair argument instead of 'Crossval'.
Estimate the k-fold margins for each classifier.
fullMargins = kfoldMargin(CVMdl); partMargins = kfoldMargin(PCVMdl);
Plot the distribution of the margin sets using box plots.
boxplot([fullMargins partMargins], ... 'Labels',{'All Predictors','10% of the Predictors'}); title('Distribution of Margins')
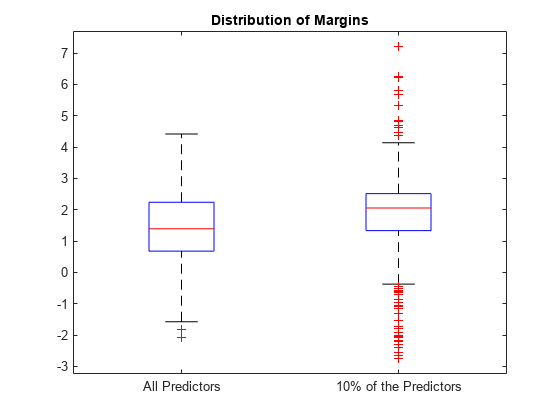
The quartiles of the PCVMdl margin distribution are situated higher than the quartiles of the CVMdl margin distribution, indicating that the PCVMdl model is the better classifier.
Input Arguments
Cross-validated, binary kernel classification model, specified as a ClassificationPartitionedKernel model object. You can create a
ClassificationPartitionedKernel model by using fitckernel
and specifying any one of the cross-validation name-value pair arguments.
To obtain estimates, kfoldMargin applies the same data used to
cross-validate the kernel classification model (X and
Y).
Output Arguments
Classification
margins, returned as a numeric vector. margin is an
n-by-1 vector, where each row is the margin of the corresponding
observation and n is the number of observations
(size(CVMdl.Y,1)).
More About
The classification margin for binary classification is, for each observation, the difference between the classification score for the true class and the classification score for the false class.
The software defines the classification margin for binary classification as
x is an observation. If the true label of x is the positive class, then y is 1, and –1 otherwise. f(x) is the positive-class classification score for the observation x. The classification margin is commonly defined as m = yf(x).
If the margins are on the same scale, then they serve as a classification confidence measure. Among multiple classifiers, those that yield greater margins are better.
For kernel classification models, the raw classification score for classifying the observation x, a row vector, into the positive class is defined by
is a transformation of an observation for feature expansion.
β is the estimated column vector of coefficients.
b is the estimated scalar bias.
The raw classification score for classifying x into the negative class is −f(x). The software classifies observations into the class that yields a positive score.
If the kernel classification model consists of logistic regression learners, then the
software applies the 'logit' score transformation to the raw
classification scores (see ScoreTransform).
Extended Capabilities
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2018bkfoldMargin fully supports GPU arrays.
Starting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.
In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)