clusterdata
데이터로부터 병합 군집 생성
구문
설명
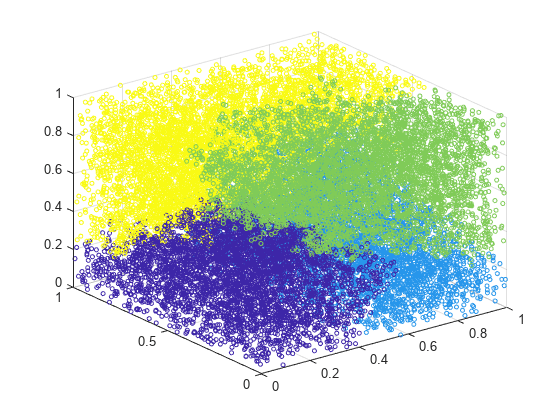
T = clusterdata(___,Name=Value)clusterdata(X,MaxClust=5,Depth=3)을 지정하면 각 노드 아래 깊이 3까지의 거리 값을 계산하여 최대 5개의 군집을 찾을 수 있습니다.
예제
무작위로 생성된 데이터 세트에서 최대 3개의 군집을 찾아 시각화합니다.
3개의 표준 균등분포에서 무작위로 생성된 데이터로 구성된 표본 데이터 세트를 만듭니다.
rng(0,"twister"); % For reproducibility X = [gallery("uniformdata",[10 3],12); ... gallery("uniformdata",[10 3],13)+1.2; ... gallery("uniformdata",[10 3],14)+2.5]; y = [ones(10,1);2*(ones(10,1));3*(ones(10,1))]; % Actual classes
데이터에 대한 산점도 플롯을 생성합니다.
scatter3(X(:,1),X(:,2),X(:,3),100,y,"filled")
최대 3개의 군집을 찾습니다.
T = clusterdata(X,MaxClust=3);
결과로 얻은 군집 할당을 사용하여 데이터를 플로팅합니다.
scatter3(X(:,1),X(:,2),X(:,3),100,T,"filled") title("Result of Clustering");
clusterdata는 데이터에서 3개의 고유한 군집을 식별합니다.
계층적 군집 트리를 만들고 군집을 찾는 작업을 한 번에 수행합니다. 3차원 산점도 플롯을 사용하여 군집을 시각화합니다.
표준 균등분포에서 생성된 20,000×3 크기의 표본 데이터 행렬을 만듭니다.
rng(0,"twister"); % For reproducibility X = rand(20000,3);
ward 연결 방법을 사용하여 생성한 계층적 군집 트리에서 최대 4개의 군집을 찾습니다. SaveMemory를 "on"으로 지정하면 거리 행렬을 계산하지 않고 군집을 생성할 수 있습니다. 그러지 않으면 컴퓨터에 거리 행렬을 저장할 메모리가 충분하지 않아 메모리 부족 오류가 발생할 수 있습니다.
T = clusterdata(X,MaxClust=4,Linkage="ward",SaveMemory="on");
각 군집을 다른 색으로 표시하여 데이터를 플로팅합니다.
scatter3(X(:,1),X(:,2),X(:,3),10,T)
clusterdata는 데이터에서 4개의 군집을 식별합니다.
입력 인수
이름-값 인수
출력 인수
팁
Linkage가"centroid"또는"median"인 경우linkage는 단조적(Monotonic)이지 않은 군집 트리를 생성할 수 있습니다. 이 결과는 두 군집 r과 s의 합집합에서 세 번째 군집까지의 거리가 r과 s 간의 거리보다 작을 경우에 발생합니다. 이 경우, 디폴트 방향으로 그린 덴드로그램에서 리프로부터 루트 노드까지의 경로는 아래쪽 방향의 일부 단계를 지나게 됩니다. 이 결과를 방지하려면Linkage를 다른 값으로 지정하십시오. 다음 이미지는 비단조적 군집 트리를 나타냅니다.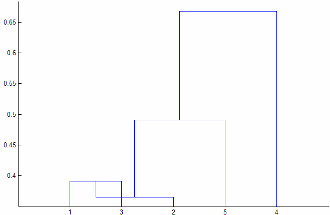
이 경우, 군집 1과 군집 3이 새 군집으로 결합되며, 이 새 군집과 군집 2 간의 거리는 군집 1과 군집 3 간의 거리보다 작습니다.
알고리즘
선택적 이름-값 인수를 지정하지 않으면 clusterdata 함수는 다음 단계를 수행합니다.
pdist를 사용하여X의 관측값 쌍 간 유클리드 거리 벡터를 생성합니다.Y =pdist(X,"euclidean")군집 간 최단 거리를 계산하는
"single"방법을 지정해서linkage를 사용하여Y에서 계층적 병합 군집 트리를 생성합니다.Z =linkage(Y,"single")cutoff를 지정하면clusterdata함수는 불일치 값이cutoff보다 작을 경우cluster를 사용하여Z에서 군집을 정의합니다.T=cluster(Z,Cutoff=cutoff)maxclust를 지정하면clusterdata함수는cluster를 사용하여Z에서 최대maxclust개의 군집을 찾고"distance"를 군집 정의의 기준으로 사용합니다.T= cluster(Z,MaxClust=maxclust)
대체 기능
계층적 군집 트리 Z(입력 데이터 행렬 X에 대해 linkage 함수를 사용하여 생성된 출력 결과)가 있는 경우, cluster를 사용하여 Z에 대한 병합 군집화를 수행하고 X의 각 관측값(행)에 대한 군집 할당을 반환할 수 있습니다.
