biplot
Biplot
Description
biplot( creates a biplot of the
coefficients in the matrix coefs)coefs. The biplot is 2-D if
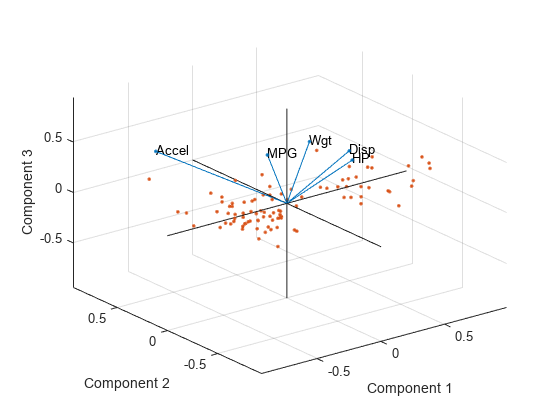
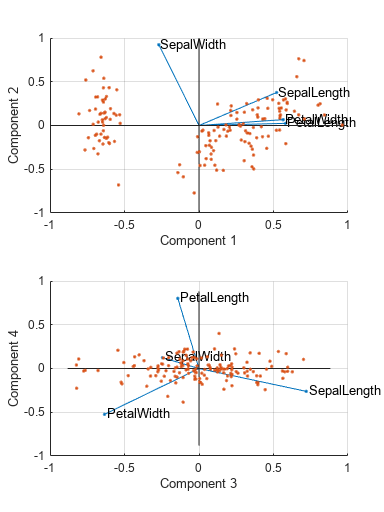
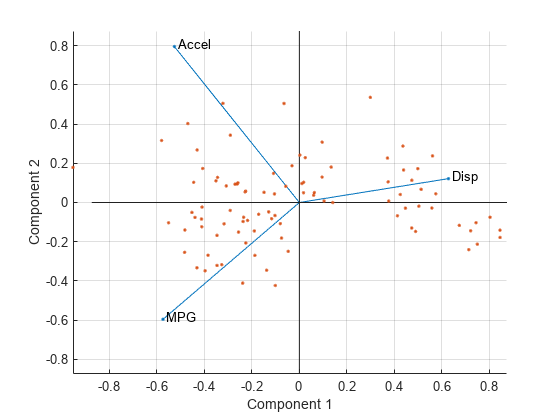
coefs has two columns or 3-D if it has three columns. The axes in the
biplot represent the columns of coefs, and the vectors in the biplot
represent the rows of coefs (the observed variables).
biplot(
specifies additional options using one or more name-value pair arguments. For example, you
can specify coefs,Name,Value)'Positive','true' to restrict the biplot to the positive
quadrant (in 2-D) or octant (in 3-D).
h = biplot(___)biplot. Use
h to query and modify properties of specific graphics objects. For
more information, see Graphics Object
Properties.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
When working with large data sets or those involving many variables, you can achieve faster performance by calling
biplotwithout assigning a graphics handle. In this case, access individual handles using their tags. For example:gca().Children
ans = 5×1 Line array: Text (varlabel) Line (obsmarker) Line (axisline) Line (varmarker) Line (varline)
h = findobj(gca,"Tag","axisline")
Set a new axis line style.h = Line (axisline) with properties: Color: [0 0 0] LineStyle: '-' LineWidth: 1 Marker: 'none' MarkerSize: 1 MarkerFaceColor: 'none' XData: [-0.9395 0.9395 NaN 0 0] YData: [0 0 NaN -0.9395 0.9395] ZData: [1×0 double] Show all propertiesh.LineStyle = ":";
Algorithms
A biplot allows you to visualize the magnitude and sign of each variable's contribution to
the first two or three principal components, and to represent each observation in terms of
those components. The biplot function:
Imposes a sign convention, forcing the element with the largest magnitude in each column of
coefsto be positive. This action flips some of the vectors incoefsto the opposite direction, but often makes the plot easier to read. Interpretation of the plot is unaffected, because changing the sign of a coefficient vector does not change its meaning.Scales the scores so that they fit on the plot. That is, the function divides each score by the maximum absolute value of all scores, and multiplies by the maximum coefficient length of
coefs. Thenbiplotchanges the sign of the score coordinates according to the sign convention for the coefficients.
Version History
Introduced before R2006a