slerp
구면 선형 보간
설명
예제
입력 인수
출력 인수
알고리즘
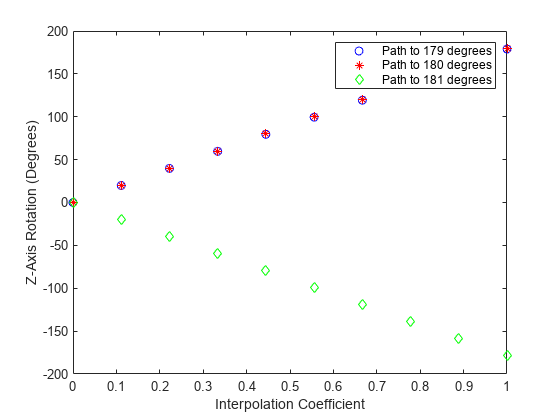
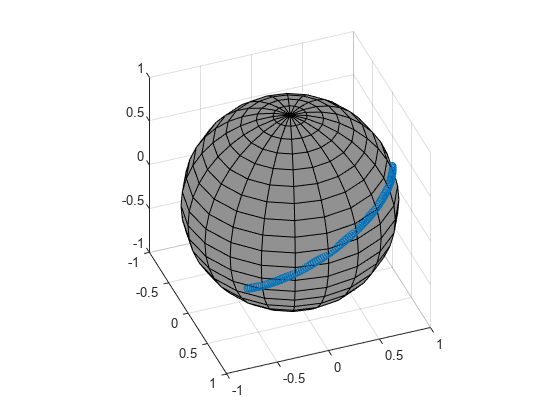
쿼터니언 구면 선형 보간(spherical linear interpolation, SLERP)은 평면에서의 선형 보간을 3차원에서의 구면 보간으로 확장한 것입니다. 이 알고리즘은 [1]에서 처음 제안되었습니다. 2개의 쿼터니언 q1과 q2가 주어졌을 때, SLERP는 q1과 q2를 연결하는 대권을 따라 새로운 쿼터니언 q0을 보간합니다. 보간 계수 T는 출력 쿼터니언이 q1과 q2 중 어느 쪽에 더 가까운지를 결정합니다.
SLERP 알고리즘은 다음과 같이 정현파로 설명할 수 있습니다.
여기서 q1과 q2는 정규화된 쿼터니언이고, θ는 q1과 q2 사이 각거리의 절반입니다.
참고 문헌
[1] Shoemake, Ken. "Animating Rotation with Quaternion Curves." ACM SIGGRAPH Computer Graphics 19, no. 3 (July 1985): 245–54. https://doi.org/10.1145/325165.325242.