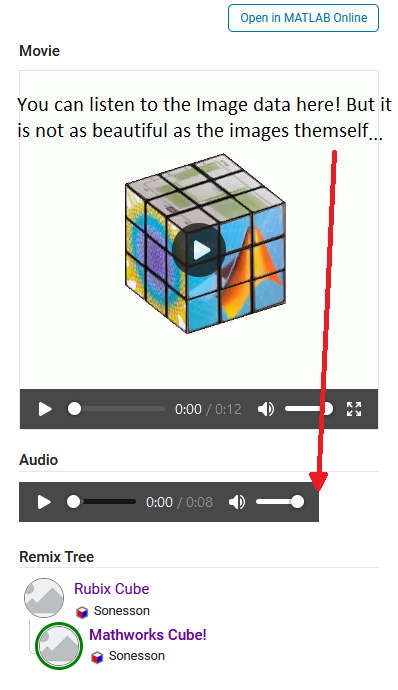
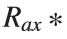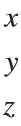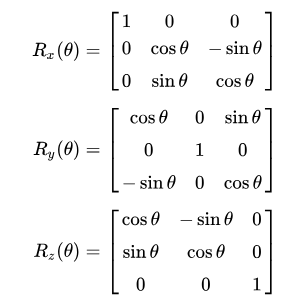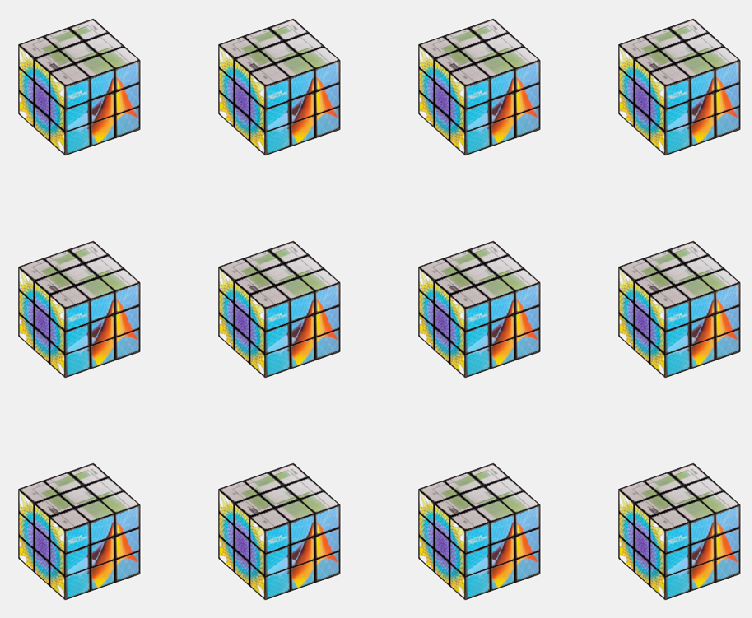About a year ago, I made a rubix cube solver with the goal of solving a cube faster than I could in real life. It was a fun and educating project, and while it is a long way from optimal, I finished with satisfying results.
How the solver is made is a story for another time, but I always wanted to have a 3D illustration of how the moves are performed to reach the solved state. Lacking the motivation at the time, the illustrative part was forgotten... Untill a couple of weeks ago when I found out about the MATLAB Shorts Mini Hack. It was the perfect motivation to finish up!
This post will detail my entry and remixes (you should check them out before reading!) in this years mini hack. I am not a man to spare any detail, and I've recently saved up a bunch of characters from being limited to 2000, so it may be a bit wordy, but I'll try to keep it entertaining. How it works, lessons learned, sidetracks, pitfalls found, and everything in between is detailed here. So feel free to peruse the sections and pick the ones that sound interesting! How can I make it move?
Intuativly one would use standard rubix notation to determine the moves, but due to the character limitation and me wanting the ability to rotate the middle rows and the cube as a whole I decided against this. At the tippy top, there is an 3xn character array, MS, containing the movement sequence of the cube. The three rows contains:
- The axis to rotate around. - Defined by character x, y, z, or p (none of them).
- The row to rotate. - Defined by character 1, 2, 3, or 4 (all of them)
- The direction of the rotation. - Defined by character n, or p (negative or positive)
The rows are ordered from largest to smallest coordinate value along the axis of rotation. If a pause is selected, the program does not really care which character is chosen for the row and direction.
"But how many moves can I make within the time?" As many, or few, as you want.
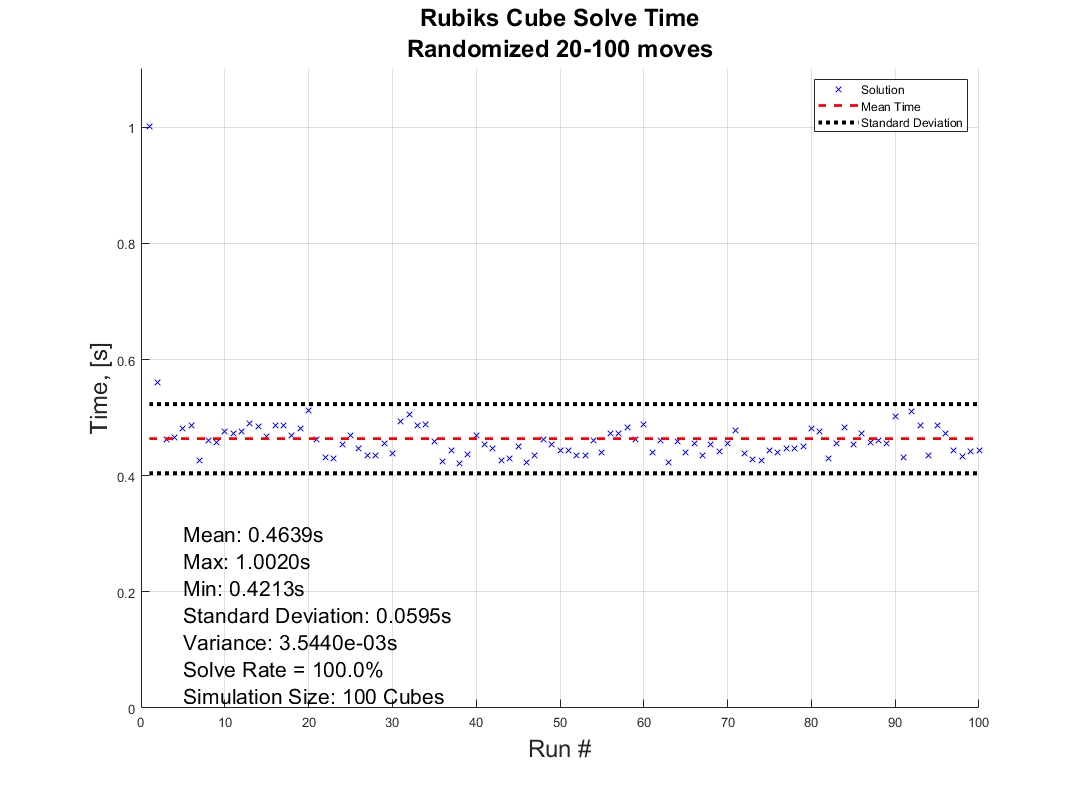
Well... As long as you want 96 or less moves that is. The function alters the angular speed of the rotations to fit them all within the 96 frame window. But since we iterate through the cube (more on that later) we need to ensure that a move has completely finished before starting another move, or the cube will start looking like a contortionist.
If there is remaining time before the 96 frames are up (due to the timing of the angular speed), the cube politely pauses and waits for the last coule of frames to pass.
The hardest part is finding a sequence short enough to not look like the cube is flailing wildly during its 4 seconds of fame, but long enough to make some interesting pattern like the tetris shuffle in my original entry! Preferably while still being a perfect loop.
Easy, right? Now go make your own!
Tip: Use the camera rotation to your advantage! Wanting to showcase all sides of the Mathworks cube for as long as possible, I needed a short movement sequence which gives lower angular speed. I cut out two moves from the sequence by making the camera rotate 180 degrees to finish my perfect loop at a different set of coordinates from where I started!
How did you make the cube so beautiful (MathWorks motive)?
A lot of credit should go to Tomoaki Takagi and his entry. I am a sucker for utilizing things for purposes they were not intended to be used for, and he did just that. We are not allowed to upload images or data in the contest. But we are allowed to optionally upload some background audio for the video. The key is to realise that this audio is stored in the same place as the contest entry. Meaning we can access the "audio.wav" file we just uploaded to the contest.
An audio file is really just a long row of values between -1 and 1. So... if one were to take a picture of every side of a MathWorks cube laying around on the desk, splice the images into 54 seperate textures, scale the intensities between 0 and 1, reshape them to a row, and save it as an .wav file using the audiowrite() function... One would have a bit too much free time, but also a terrible sounding audio file with image data encoded.
There is one small problem however. As you might have noticed, the audio of most entries sound... rough. This is because of an file compression (or something of the like) applied to files over a certain length when you upload them to the contest. This also applies to audio files filled with image data that does not take particularly well to getting squeezed.
The solution? Compress it yourself (carefully)! Again I looked at Tomoaki's entry, to see what length worked for him. His entry contained a 150x150x3 image upscaled by a factor 4. His image is not exactly sharp, and with 54 different textures needed for a cube, each side would be... about 3x3x3. While a bit poetic, we can not bring such dishonour to such a beautiful object! Luckily Tomoaki had not used the entire audio file for image storage. And he used mono sound (1 audio channel) for his entry and .wav files support stereo sound (2 aoudio channels) meaning I could utilize twice as much space netting me a neat, decent resolution of 28x28 pixels per face!
Don't forget to overwrite the audio on the last frame using audiowrite() however! Most people don't appreciate the sound of images. You should explore Tomoaki's entry for more information on this. The entry is short and easy to understand.
Summary: The audio file uploaded can be used to store image data instead of sound data. Just be careful about file length and size as compression won't treat you kindly!
How did you build the cube?
Excellent question, my dear watsson. Surfaces. Lots and lots of surfaces. This part is takes the most computation time. If anyone has some forbidden knowledge I don't know about here, feel free to correct and enlighten me!
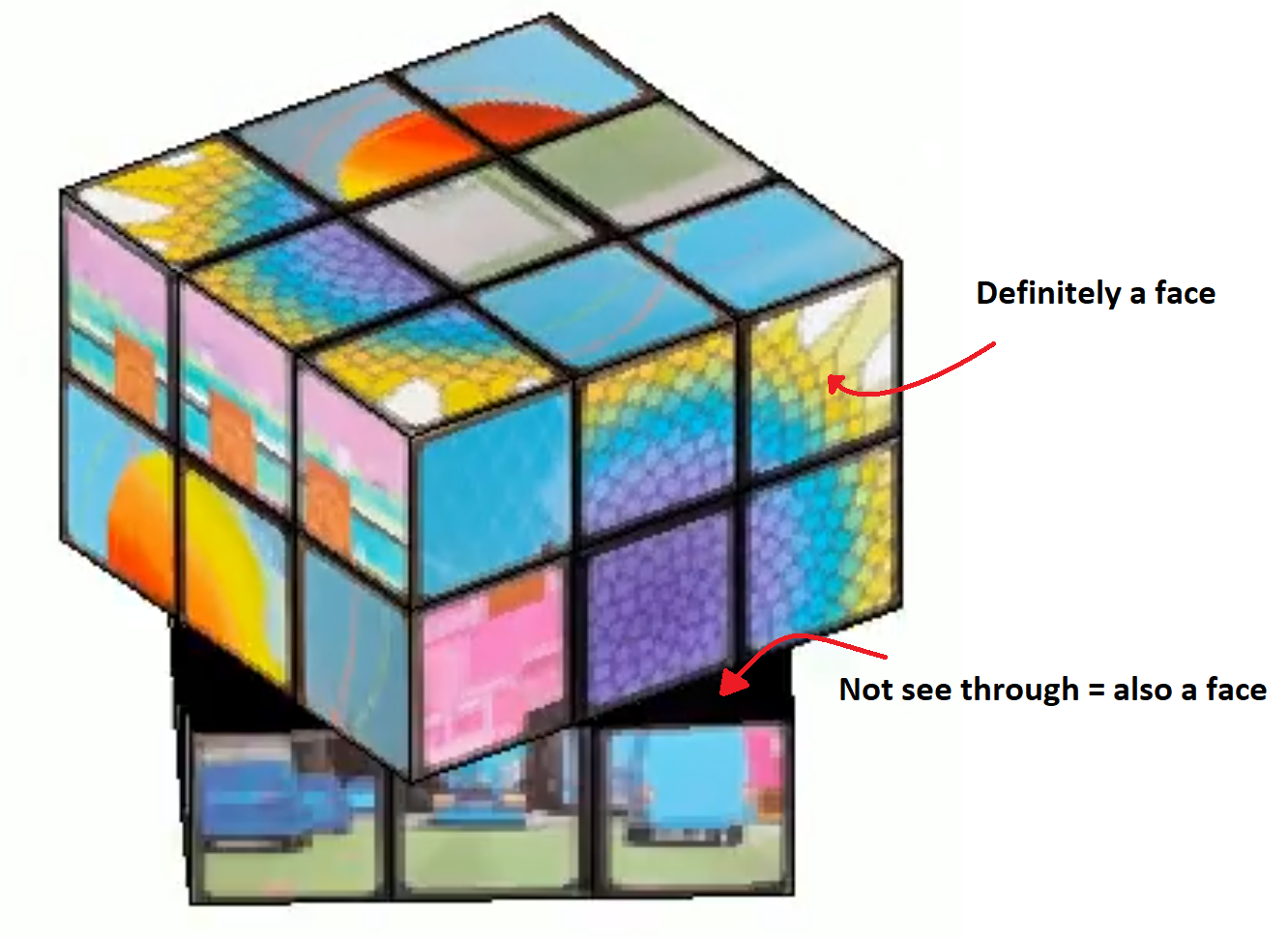
We want to be able to assign each face of the cube a seperate texture, and to be able to move each face seperately without it morphing itself or other parts of the cube. Because of this, they can't be part of a meshgrid connecting each other. Instead we have to construct each surface individually. This takes a second, but is much better in my latest version (See more in the I crave speed section). Which in my earlier entries was a big deal because I was yet to learn about our lord and saviour, persistent variables through Timothy's beautiful entry: Refraction. One could think a rubix cube has 54 faces, 9 on each side, but alas that is but an illusion. A rubix cube is infact 27 (26 if not counting the center) smaller cubes in a trench coat. Each with 6 sides. (As illustrated by William Dean's entry Is this cheating? posted while I'm writing this, thanks for the assist!). Patch objects are all good and well when creating faces if you only want colors, which is the case in my first submission. But MATLAB surface objects are also 3D and have a property that allows them to be textured which we use in the later versions.
Thinking about the trench coat covered cubes, we can tell that on a physical cube we have 6 planes in each coordinate direction. 2 for each row of cubes. The faces pointing outward are textured and the faces pointing inward are typically black. That is how we will model our cube as well.
The above image shows how the cube looks during the process of building each face. You may think to yourself "Why do you only have 4 planes in a direction? Do we really need all 6 that you mentioned?" Yes. and if you could enhance and zoom the image like the movies, you would see a tiny gap between the "2" black central planes (this is a surprise tool that will help us later!). The 6 planes are necessary to cover up the cube's hollow interior from multiple viewing angles so we can not compromise it down to 4. Imagine flippnig the cube in the first image of this section and looking into the cube. If we had 4 planes, we would be able to see through the cube from one of the angles.
Summary: We imagine the cube as 3x3x3 smaller cubes. We build each side, inwards pointing or not. We make each face of these smaller cubes seperately using surface() to avoid morphing behavior and to allow the surfaces to be textured individually.
How does it move?
The trick is all about coordinates. Firstly, to make the cube move we need a couple of things:
- Some indicator of how and what to move (a movement sequence, MS)
- The speed at which it should move
- A way to separate what verticies should and should not move
- An operation to transform the coordinates of said verticies so they move
- And of course we need to update the existing data and plot.
We are already familliar with the movement sequence from the first section, so I will spare you the repetition.
The speed of rotation is fairly simple, we have a number of moves defined in MS, and a number of frames to play with, 96. Simply find how many frames we can afford to allocate each move, 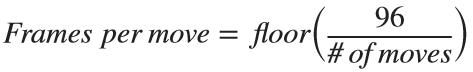 and since each "rotation" of the cube is a quarter turn (
and since each "rotation" of the cube is a quarter turn ( ) we get
) we get  . Pretty straight forward.
. Pretty straight forward.
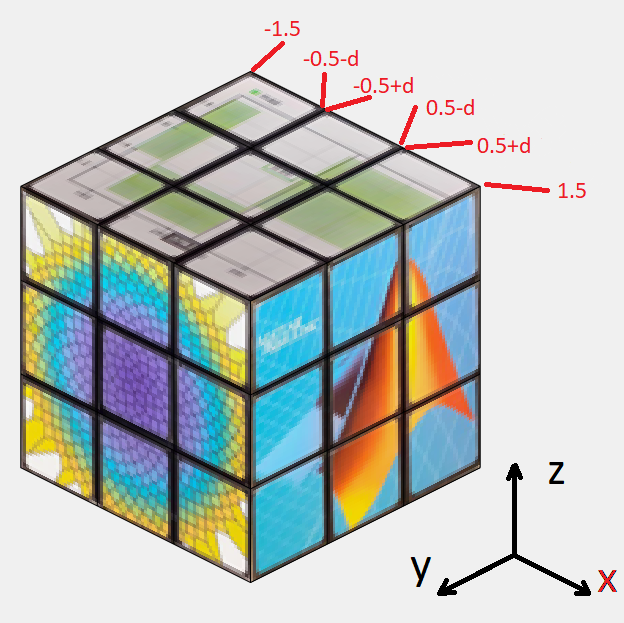
Now we need to know which verticies should and should not move. Here we use our surprise tool from the previous section! When building the cube, we add a slight offset separating the central planes. We can use this coordinate shift to separate the different planes from eachother. This would not be entierly possible if the central planes shared coordinates.
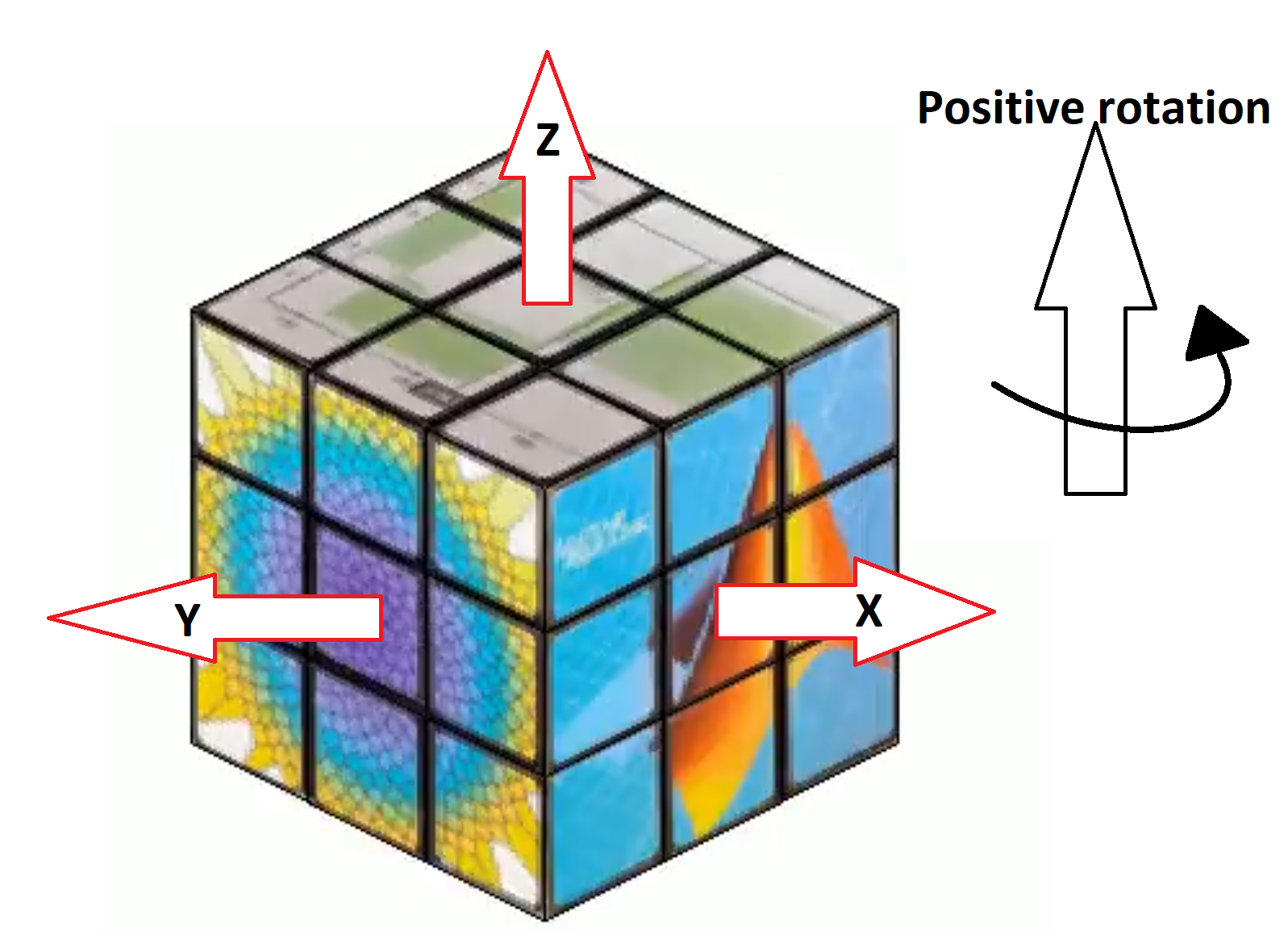
As an example, let's say the movement sequence dictates that we should rotate around x and we should choose the first row. Since the cube is centered around 0 and the planes have coordinates:
in all directions where δ is the small offset, we can easily seperate the first row by checking which faces have x coordinates higher than 0.5 in all 4 verticies. Simmilarly we check for 4 verticies in between ±0.5 for the 2nd row and values lower than -0.5 for the 3rd row. For rotating the entire cube, we can just select all faces. This works for all coordinate axis due to the symmetry that occurs when being centered around 0.
Now we need an operation to transform the coordinates of the verticies. We want to rotate some 3D coordinates around a specified coordinate axis. Sounds like the perfect job of a rotational matrix for me. This is why you stay in school kids.
In case someone has never heard of a rotation matrix before, on the assumption that anyone using Matrix Laboratory is probably familliar with matrix math and basic linear algebra I'll keep this short. Basically, there are some standard matrices that will rotate a point [x,y,z] arount the origin of an axis. such that
Where the subscripts r denotes the rotated coordinates and ax the axis to rotate around.
These matricies are as follows:
Where θ is the angle with which you rotate the point. In our case the Angular speed.
Now, I define my own rotation matrices. This is because of one of three reasons:
- MATLAB does not have rotation function which rotates a point around a specified axis (this would baffle me)
- I am blind and could not see the correct function in the documentation (plausible)
- I am illiterate and can not read the documentation (improbable)
So we have everything we need! We just update the coordinate data of the affected surface objects, slap down a drawnow command for good measure, and call it an iteration!
But I'd like to shine light on something that is both feature and flaw before we move on. 24 frames per second looks decent enough, but trained eyes can tell it is a bit choppy. Especially when things move fast. So we would like our movement as slow as possible. "Then why does the angular speed as defined above not always utilize all 96 frames to finish the movement sequence?" Because to a trained eye, what looks even more choppy is a rotation not finishing before another starts as the image shows below with a frame by frame on this effect.
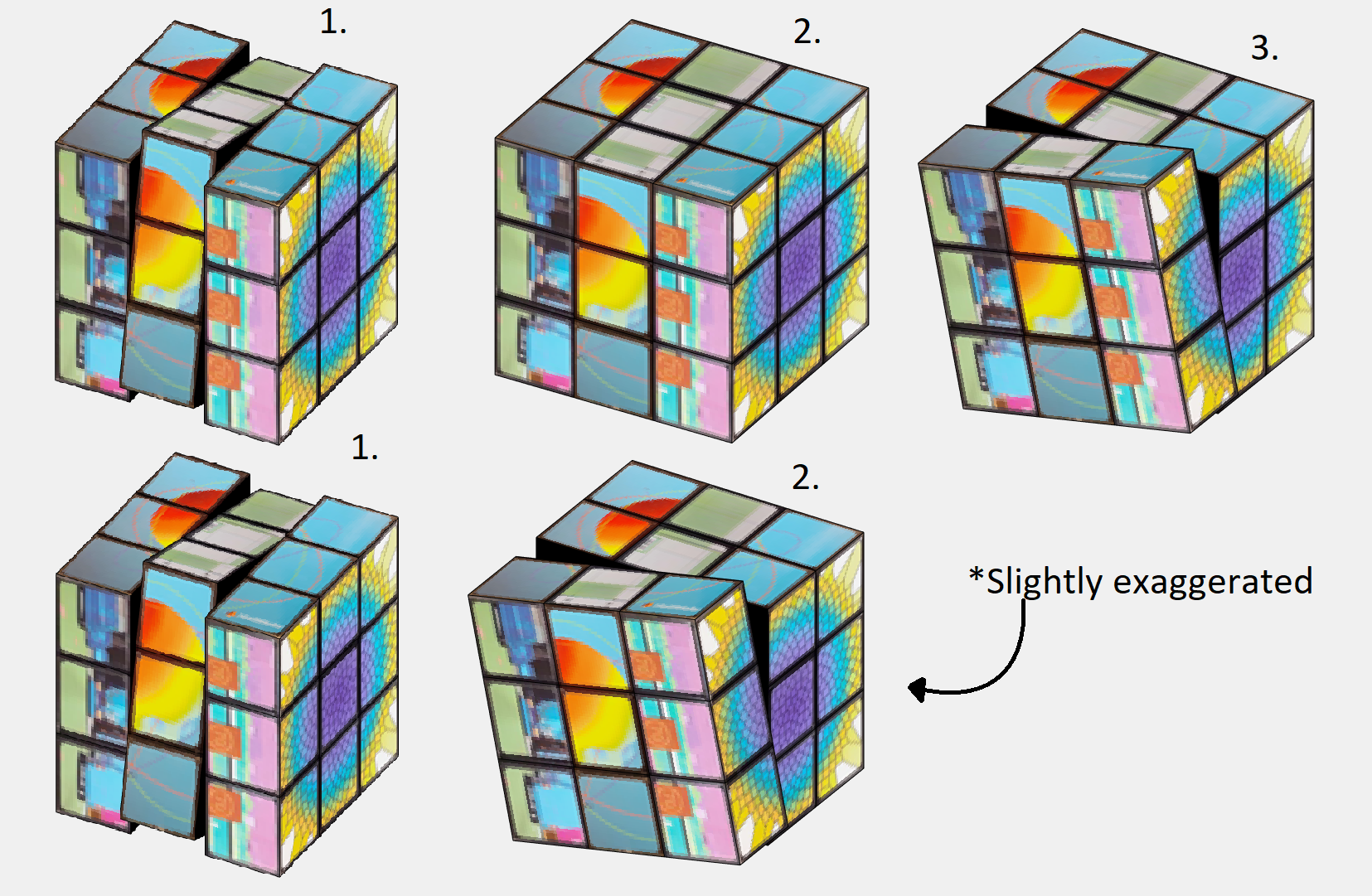
By matching the angular speed to an integer number of frames (by using floor()) for each rotation, we will always complete the entire rotation before starting the next move.This is good because of the reason mentioned above (it looks better), but also because we will base the next rotation on the coordinates of the current position. So it also saves us having to do some extra math to get everything aligned and in position to select the correct faces every time we swap move.
Summary: We use a combination between clever choice of coordinates and some standard rotational matricies to shift the relevant verticies as dictated by the movement sequence by an angle. Being carefull to make each rotation precisely end on an integer number of frames so that the same method works next time.
I crave speed!
Well buckle up then bucko! Best part about programming is that the instant after you spend time making something, you learn something that trivialises it. Persistent variables were that for me this project. My 3rd remix is all about making it faster (in the works as we speak)! You know what they say; "Make it work, make it good, make it fast".
My biggest qualm about my earlier versions was the execution speeds. Every call of drawframe, I would have to rebuild all my surface object to make the cube and re-iterate all the movement of the cube up untill the current frame to ensure the rotations of all verticies, and thus faces, are correct.
Defining a variable as persistent allocates it's memory in a way that it is not removed between function calls. Perfect for being limited by 96 calls to the same function that does not accept iterative input.
Without persistent variables, we needed to remake the surfaces each call to drawframe. Worse still; since we dont know the positions of the surfaces in the previous frame, we also had to re-iterate all the movement of the cube. You may ask yourself "why could you not just calculate the surface position based on the frame, angular speed of rotation and previous moves?". While the position of each face is possible to anticipate effectively with a look up table (which would not fit in the character limit but could have been snuck in with the image data), the rotation of each face is a bit more complex to keep track of. Not an issue with plain colors, but a challange when using textured faces.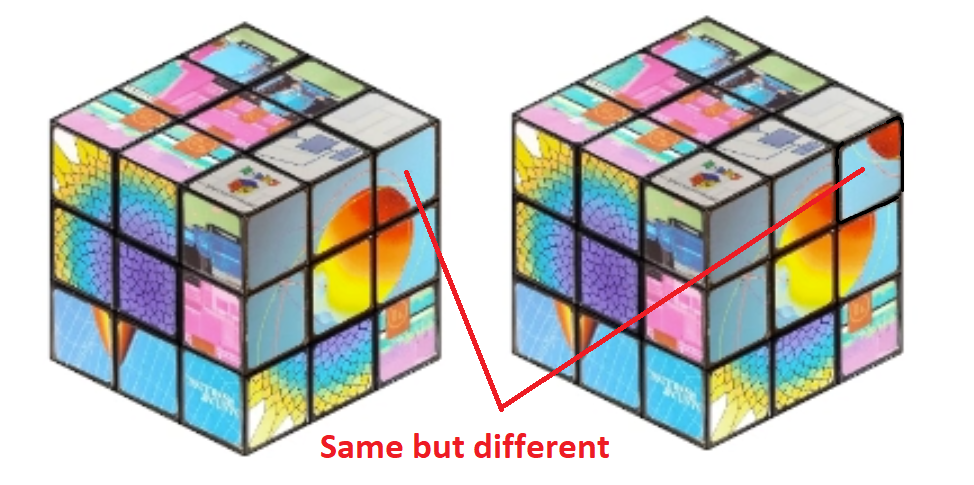
Using persistent variables as in my latest version solves theese two issues and makes the code run silky smooth compared to earlier. It now
- Removes the most time consuming part (creating surfaces) 95 out of 96 times, and
- Removes the need of re-iterating through all movement to catch up with all the rotations previously made.
It does however remove a neat function of the code; frame independency. The competition calls drawframe 96 times with the numbers 1:96, so frame independency it is not an issue as the previous frame is always the previous frame. However, if we now were to call the drawframe function with the values 1, 5 ,and 96, we would not recieve frame number 1, 5, and 96 of the animation as we would have before. Now there is an implicit need to call the function in with the frames in order.
An interesting thought that occured to me was; "If I can store the surface object in a variable, why could i not just copy it to another variable and edit it's properties instead of making a gazillion calls to surface()?" Well, turns out that is not possible because the surface object as stored in the workspace is really more of a pointer to the memory storing the object in the figure window rather than the value in the memory itself. If you copy surface_1 to surface_2 and change surface_2: you get the same change in surface_1.
Also, you might think;
"EWWW... I see nested for loops."
Yep. Is creating the coordinates for the surfaces vectorizable? Absolutely. Not even that hard either. Use combinations() with the possible x, y, and z coordinates and you got yourself the coordinates to every vertice of the cube. Use some fancy logic to determine which vertice goes where and vóila: all verticies neatly ordered ready to be made into surface objects. You could probably even use meshgrid() instead if that is more to your liking. The issue lies in the "made into surface objects" part. As stated, the repeated surface call is still needed to obtain seperate parts of memory to store the surface objects. You would still need as many loop iterations, though not nested. So I decided to leave the nested loops, as a treat, because it made it easier to determine the order and orientations of the textures when encoding them into the audio. After all, efficient coding is not only about the execution speed of the code, it is also about the writing speed of the coder. Or as textbook authors would say: "This is left as an excercise to the reader".
"Are all the inner planes necessary?"
Almost. We need 6 planes for the cube to not look hollow, but since the entire inside plane is black could we not just make it one big surface? No. Different part of the planes move with different rotations, and so can eventually end up as a part of another plane. To avoid morphing, they can not be connected. Also if the planes were solid, we would rotate into still standing planes when a row is angled (kind of like the black parts of the contorted cube earlier). However, we technically do not need the center of the 27 cubes in any scenario, and we could write some logic to not include those specific faces. This was not done for character limitation purposes. I figured that the slight tank in speed would be outweighed by the clean looks and the potential that you, the reader, could achieve when remixing this entry with those sweet sweet roughly 30 extra characters.
"Wait, are you looping... backwards?"
Yes! Looping backwards is a pretty neat trick. In this application it is mainly used to save characters, but runs in roughly the same time as a typical explicit preallocation would.
It works bacause we allocate the first loop value in the last variable element. It is the same principle as writing:
a(5) = 5
a =
0 0 0 0 5
<mw-icon class=""></mw-icon>
<mw-icon class=""></mw-icon>
As you can see MATLAB will allocate memory for a 5 element vector despite us only specifying one element. So if we start from the back, MATLAB will do the front for us!
And here you can see how it holds up to not preallocating/typical allocation. Plus it gives the same result!
toc
Elapsed time is 0.012242 seconds.
toc
Elapsed time is 0.005438 seconds.
toc
Elapsed time is 0.001842 seconds.
Summary: Persistent variables are really neat They keep their values between calls to functions. In terms of this contest they remove the need to re-iterate things, or for you to keep the state of the last frame without the need for rebuilding it every time.
Surface objects in the workspace are really just pointers to the surface objects in the figure window. This means that we unforttunately must call surface() for each face we want to create.
While initiating the surfaces, I use nested loops. Unnesting these loops is very doable with combination() and left as an excercise to the reader. You will still need the same total number of loop iterations to create all the surface objects, and the loops make texturing more convinient.
All 6 planes are necessary, but the central face of each "inside" plane is redundant and could be skipped at the cost of some additional logic.
Looping backwards is a cool trick to make MATLAB perform the preallocation of memory for you when iterating through a variable.
You get a cube, and you get a cube, and...
As earlier stated, in the "I crave speed!" section my 3 entries happen to follow the "Make it, make it good, make it fast" rule. But I did not just want to upload something that did not add more than just having cleaner code. There is a whole artistic and visual part to it all. So I thought to myself, why not use the speed? Now that the thing is running smooth, why not just run it twice? So i did just that. Except, simmilar results could be achived with much less grief if I just... Made the illusion that I ran it several times in parallel. I wanted to show of the improved speed with making more cubes, but... Why not just copy the cube? So I did that insead!
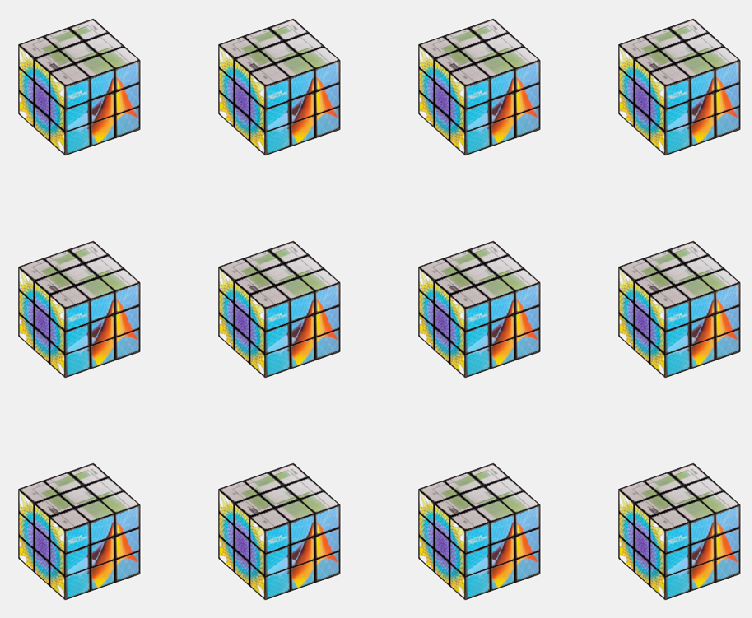
The figure window i really just an interactive image. using getframe()and frame2im() we can quickly turn whatever is shown in the current figure into an image stored in a workspace variable. From here we just need to display that same image multiple times in a sort of array. repmat() in combination with imshow() could have been used here (and would probably have been a bit more flexible in deciding how the cubes are displayed) but I opted for storing the image in a cell array of desired size and using montage() instead.
Most people being character limited in this competition keep everyting to a minimum including the figure windows. Yet I have two of those in my last entry despite only one being shown. As stated in the previous section, surface objects in the workspace is really more of a pointer to the object in the figure, so to keep all my surfaces in between runs I need the figure window containing my surface objects undisturbed. which is why I place the montage in a seperate figure. and display that at the end instead.
An interesting feature *cough* bug *cough* is the swapping between the figure windows that appear in the video generated. This is because of using return as various points in the code in order to skip computations if the move is a 'pause'. The code then does not reach the point where the figure is swaped and montage is made. I thought this to be visually interesting and is therefore dubbing this bug a feature and leaving it in!
Summary:
Multiple cubes were achived by taking the 'image' displayed by the plot window and creating a montage with several of them in a seperate figure window. The swapping between the single and multiple cube view is made by selecting the active figure window before the end of the drawframe call!
Bye for now!
I have yapped on for far too long. Hope you learned something, and thank you all for the kind words and positive response to my entry. This project has been a blast!



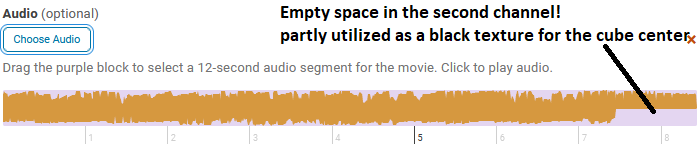

 ) we get
) we get  . Pretty straight forward.
. Pretty straight forward.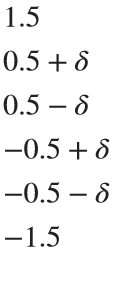
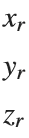 =
=