웨이블릿 신호 분석기
설명
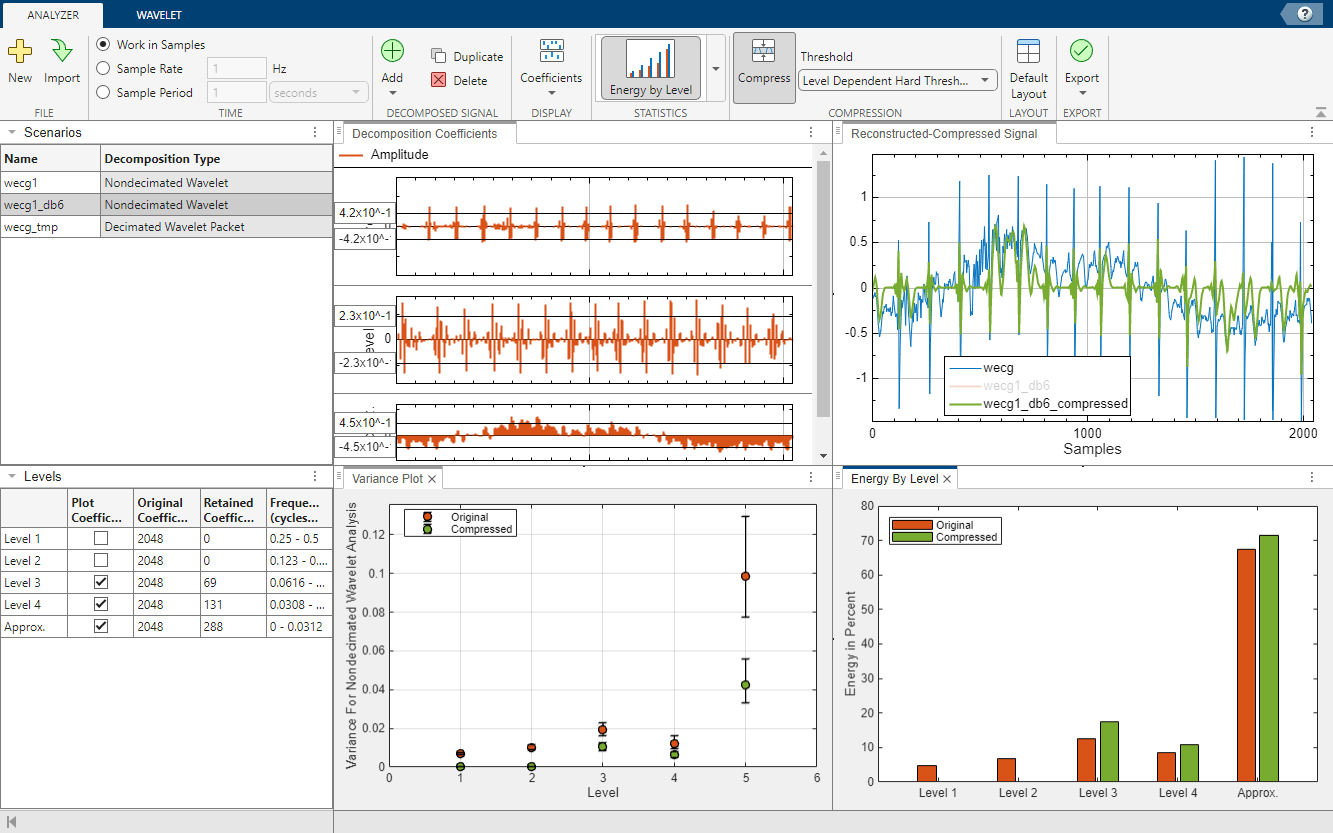
웨이블릿 신호 분석기 앱은 데시메이션되거나 데시메이션되지 않은 이산 웨이블릿 및 웨이블릿 패킷 변환을 사용하여 1차원 신호를 시각화, 분석, 압축할 수 있게 해줍니다. 이 앱은 신호의 분해와 그에 대응하는 복원을 플로팅합니다. 이 앱은 각 성분의 대략적인 주파수 대역을 포함한 분해 통계량도 보여줍니다. 웨이블릿 신호 분석기 앱을 사용하여 다음을 수행할 수 있습니다.
MATLAB® 작업 공간에서 모든 단일채널 신호, 1차원 실수 값 및 복소수 값 신호에 액세스합니다.
웨이블릿 또는 분해 레벨을 변화시키면서 다양한 분석의 분해를 비교합니다.
시간 정렬 계수를 시각화합니다.
웨이블릿 변환을 계산하기 전에 주기적으로 또는 반사를 통해 신호를 확장합니다.
전역 임계값 또는 레벨 종속 임계값을 분해에 적용하여 신호를 압축합니다.
분해의 통계량을 시각화하고 압축이 이에 미치는 영향을 살펴봅니다.
모든 분해 레벨에 대해 에너지를 플로팅합니다. 데시메이션되지 않은 웨이블릿 분해의 경우 계수의 분산을 플로팅할 수도 있습니다.
지정한 분해 레벨에 대해 계수의 자기상관과 히스토그램을 표시합니다.
분해 계수, 압축 계수, 압축 신호를 MATLAB 작업 공간으로 내보냅니다.
작업 공간에서 결과를 재현하기 위해 MATLAB 스크립트를 생성합니다.
웨이블릿 신호 분석기 앱은 단정밀도 데이터와 배정밀도 데이터를 지원합니다.
웨이블릿 신호 분석기 앱 열기
MATLAB 툴스트립: 앱 탭의 신호 처리 및 통신에서 앱 아이콘을 클릭합니다.
MATLAB 명령 프롬프트:
waveletSignalAnalyzer를 입력합니다.
예제
프로그래밍 방식으로 사용
팁
다중채널 신호의 채널 하나를 분해하려면 해당 채널을 프로그래밍 방식으로 가져오십시오. 예를 들어, 다음 명령을 사용하여 다중채널 Espiga3 EEG 데이터 세트의 열 번째 채널을 분해합니다.
load Espiga3 waveletSignalAnalyzer(Espiga3(:,10))여러 다른 1차원 신호의 잡음을 동시에 제거하려면 웨이블릿 신호 분석기의 인스턴스를 여러 개 실행하십시오.