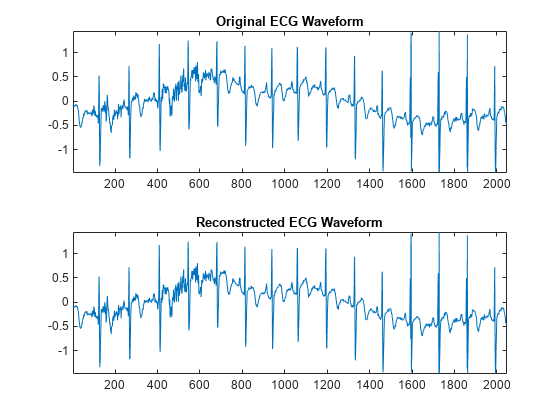
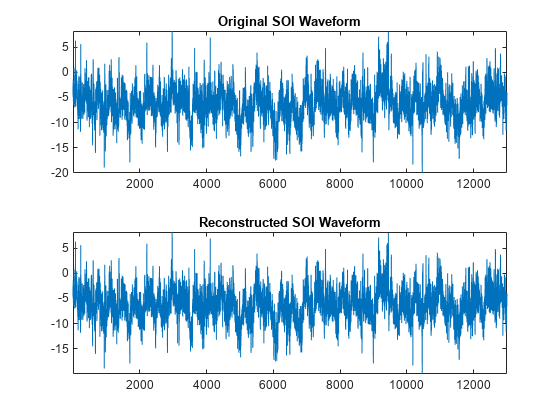
imodwpt
Inverse maximal overlap discrete wavelet packet transform
Description
Examples
Input Arguments
Output Arguments
References
[1] Percival, Donald B., and Andrew T. Walden. Wavelet Methods for Time Series Analysis. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge ; New York: Cambridge University Press, 2000.
[2] Walden, A. T., and A. Contreras Cristan. “The Phase–Corrected Undecimated Discrete Wavelet Packet Transform and Its Application to Interpreting the Timing of Events.” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 454, no. 1976 (August 8, 1998): 2243–66. https://doi.org/10.1098/rspa.1998.0257.