Estimate Spectral Model
Description
The Estimate Spectral Model task lets you interactively estimate and plot a spectral model using time data. You can specify one of three estimation algorithms and modify the size of the window size that determines frequency resolution. You can also specify the frequency vector, including the number of frequencies and whether those frequencies are evenly spaced on a linear or a logarithmic scale. The task automatically generates MATLAB® code for your live script. For more information about Live Editor tasks in general, see Add Interactive Tasks to a Live Script.
A frequency-response model is the frequency response of a linear
system evaluated over a range of frequency values. The model is represented by an idfrd model object that stores the frequency response, sample time, and
input-output channel information. For more information about frequency-response models, see
What Is a Frequency-Response Model?.
The Estimate Spectral Model task is independent of the more general System Identification app. Use the System Identification app when you want to compute and compare estimates for multiple models.
To get started, load experiment data that contains input and output data into your MATLAB workspace and then import that data into the task. Then, specify a model structure to estimate. The task gives you controls and plots that help you experiment with different model parameters and compare how well the output of each model fits the measurements.

Open the Task
To add the Estimate Spectral Model task to a live script in the MATLAB Editor:
On the Live Editor tab, select Task > Estimate Spectral Model.
In a code block in your script, type a relevant keyword, such as
spectralorestimate. SelectEstimate Spectral Modelfrom the suggested command completions.
Examples
Use the Estimate Spectral Model Live Editor Task to estimate a frequency-response model and plot the response.
Set Up Data
Load the measurement data tt2 into your MATLAB workspace.tt2 is a timetable that contains one input variable u and one output variable y.
load sdata2 tt2
Import Data into Task
In the Select data section, for Data type, select Timetable. For Estimation data, select Input-output data. In Timetable, select tt2.
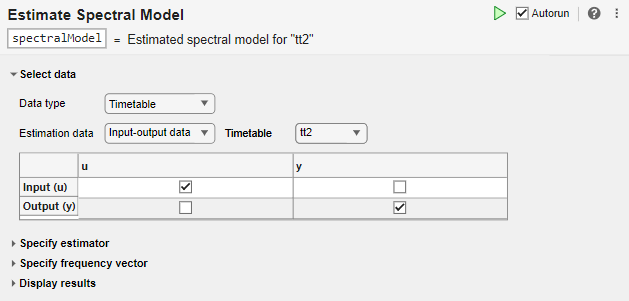
The task displays a table that contains the tt2 input and output variable names.
Estimate Model Using Default Settings
The default algorithm is SPA (Blackman-Tukey).
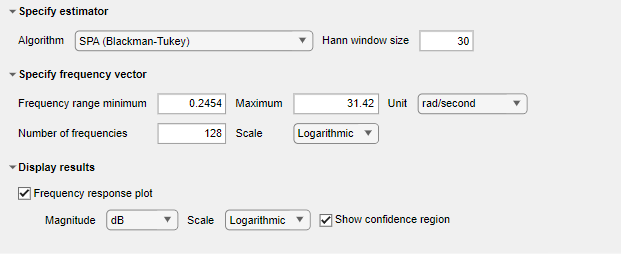
Because Autorun is selected, the task automatically performs the estimation, using this algorithm and the default settings for Specify frequency vector and Display results.
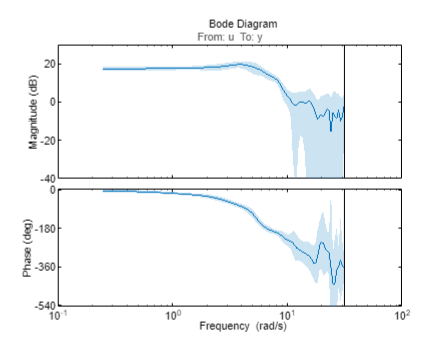
Examine Plot
The task displays a Bode plot that includes a confidence region of three standard deviations.
View Code
To display the code that the task generates, click ![]() at the bottom of the parameter section. The code that you see reflects the current parameter configuration for the task.
at the bottom of the parameter section. The code that you see reflects the current parameter configuration for the task.

Parameters
Select Data
The task accepts numeric measurement values that are uniformly sampled in time.
Input and output signals can contain multiple channels. Data can be packaged either as
numeric arrays (for Numeric), in a timetable (for Timetable), or in an iddata object (for Data object).
The data type you choose determines whether you must specify additional parameters.
Numeric— Specify Sample Time in the time units that you select.Timetable— Specify no additional parameters because the timetable already contains information on time sampling.Data Object— Specify no additional parameters because the data object already contains information on time sampling.
The task accepts input-output data and time series data that has no input array.
The estimation data content you select, along with your selection of Data Type, determines your options for accessing variables from your MATLAB workspace.
Input-Output DataNumeric data — Select the variable name of the for your input and output vectors for Input (u) and Output (y), respectively.
Timetable — When you specify a timetable, the task displays the timetable variables and the default assignment of the variables to input and output signals. You can change these assignments by selecting different variables.
Data object — Select the data object.
Time seriesNumeric data — Select the variable name of your output vector for Output (y).
Timetable — The task assumes that all the variables in the timetable are output signals and selects them as Output (y). Clear the selections for variables that represent inputs.
Data object — Select the data object.
Specify estimator
The task provides three algorithms to choose from.
SPA— Blackman-Tukey Spectral analysis (SPA) method. Takes the Fourier transform of windowed versions of the covariance function.SPAFDR— Variant of the SPA method that uses frequency-dependent resolution.ETFE— Empirical transfer function estimate. This method computes the ratio of the Fourier transform of the output to the Fourier transform of the input. For time series, which have no input, this method computes a periodogram as the normalized absolute squares of the Fourier transform of the time series.
For more information on these algorithms, see spa, spafdr, and etfe. For information on selecting an algorithm, see Selecting the Method for Computing Spectral Models.
Each estimation algorithm uses a unique parameter for determining and using the window size.
SPA— Hann window size. Specify this parameter as a positive integer greater than 2. The default value is equal to 30 for data arrays with lengths of 300 or more, or, for smaller arrays, arraylength/10.SPAFDR— Resolution. Specify this parameter in rad/TimeUnit, whereTimeUnitis the unit you specify for Sample Time. The resolution is the size of the smallest detail in the frequency function and the spectrum that is resolved by the estimate. Setting the resolution is a tradeoff between obtaining estimates with fine, reliable details, and suffering from spurious, random effects. The default value in the task isdefault, which uses the resolution thatspafdrcalculates based on the frequencies. If you want to view this resolution value for the SISO modelspectralModel, at the command line, enterspectralModel.Report.WindowSize.ETFE— Hamming window size. Specify this parameter, which represents frequency resolution, as a positive integer greater than 2. The value of the parameter determines the amount of smoothing that the function applies to the raw spectral estimates. The default value in the task isdefault, which uses the resolution thatetfecalculates based on the frequencies. If you want to view this resolution value for the SISO modelspectralModel, at the command line, enterspectralModel.Report.WindowSize.
Specify frequency vector
Specify the frequency vector minimum and maximum, and select the unit, such as the
default rad/second, from the Unit list.
By default, the task sets the frequency to span the range bounded at the upper end by
the Nyquist frequency, which is a function of the sample time. The task sets the default
value of the lower end of the range to the first frequency value.
Specify the number of frequency divisions and whether to use a linear or a
logarithmic scale. The default number of divisions is 128. The
default scale is Logarithmic.
Display Results
Select Frequency response plot to create a frequency plot of
your model. If you specify your data type as Input-output data, then
the task creates the frequency response using bode. If your data type is Time series, then the task
plots the power spectrum using spectrum.
You can plot only one model at a time in the task. If you want to compare responses, do one of the following:
Open multiple tasks and visually compare plots for different models.
Use unique model IDs for each model you want to compare, and then create Bode plots for them at the command line.
Specify the parameters for the Bode or power spectrum plot. You can specify that the units in Magnitude are dB or absolute value. For Scale, you can specify a logarithmic or a linear scale for the frequency axis. If you are creating a Bode plot by using input-output data, you can select Show confidence region to display a confidence region of three standard deviations. If you are creating a power spectrum plot by using a time series, no Show confidence region option exists.
Version History
Introduced in R2021bThe task is updated to accept time-domain data in the form of a timetable. The task
continues to accept numeric time-domain data as well, with the
Numeric data type option.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)