웨이블릿 시간-주파수 분석기
설명
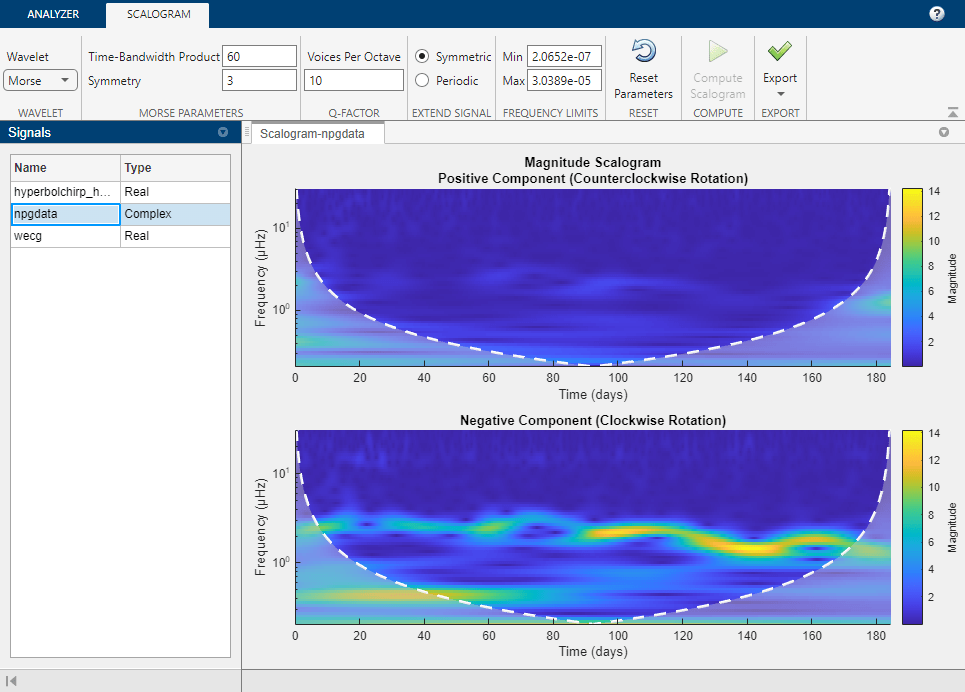
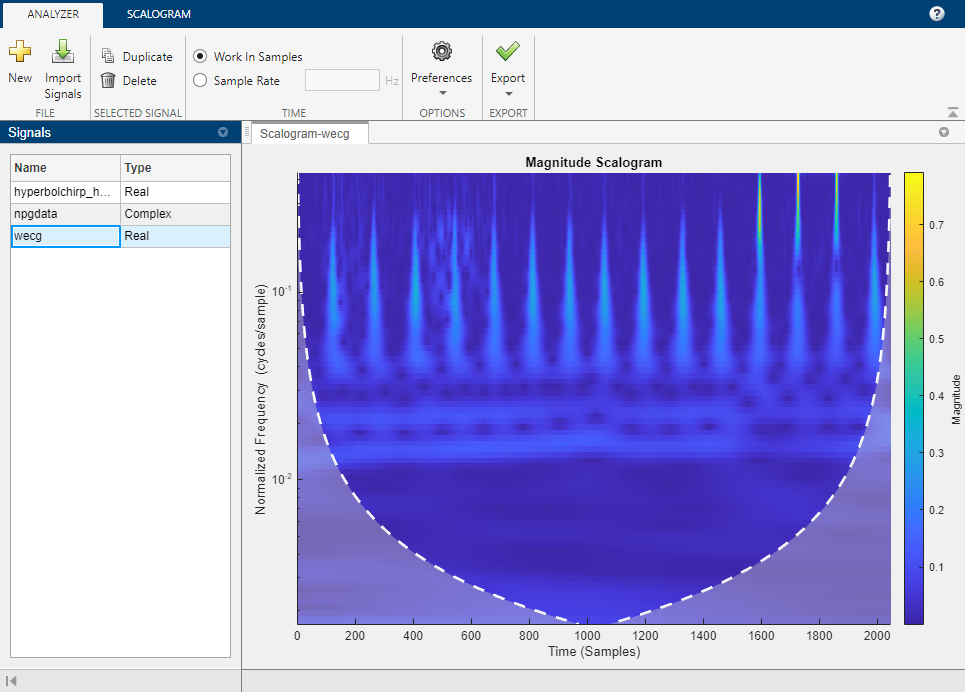
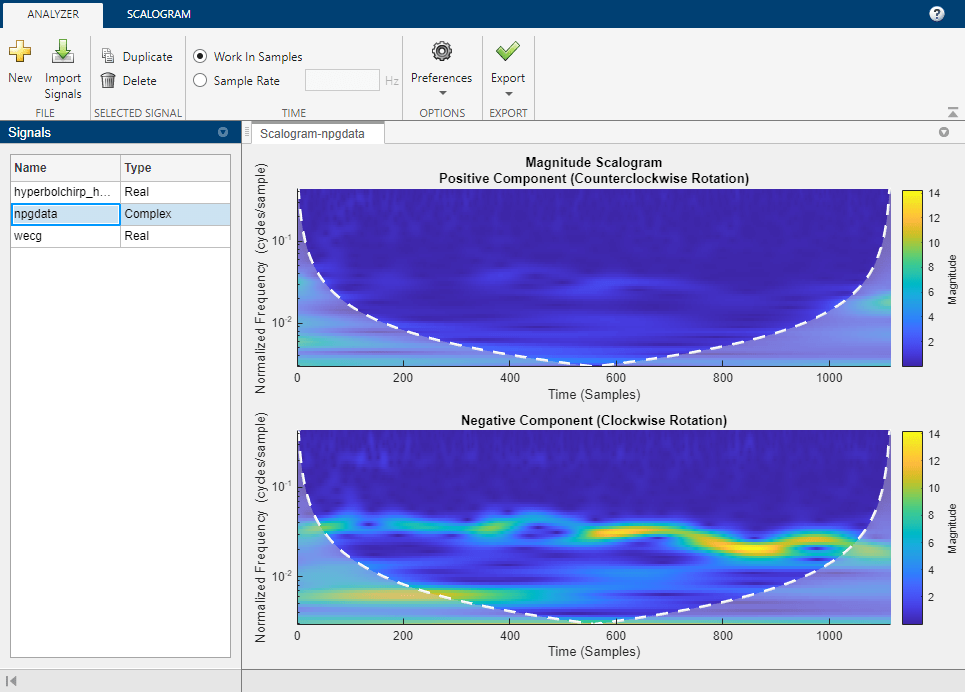
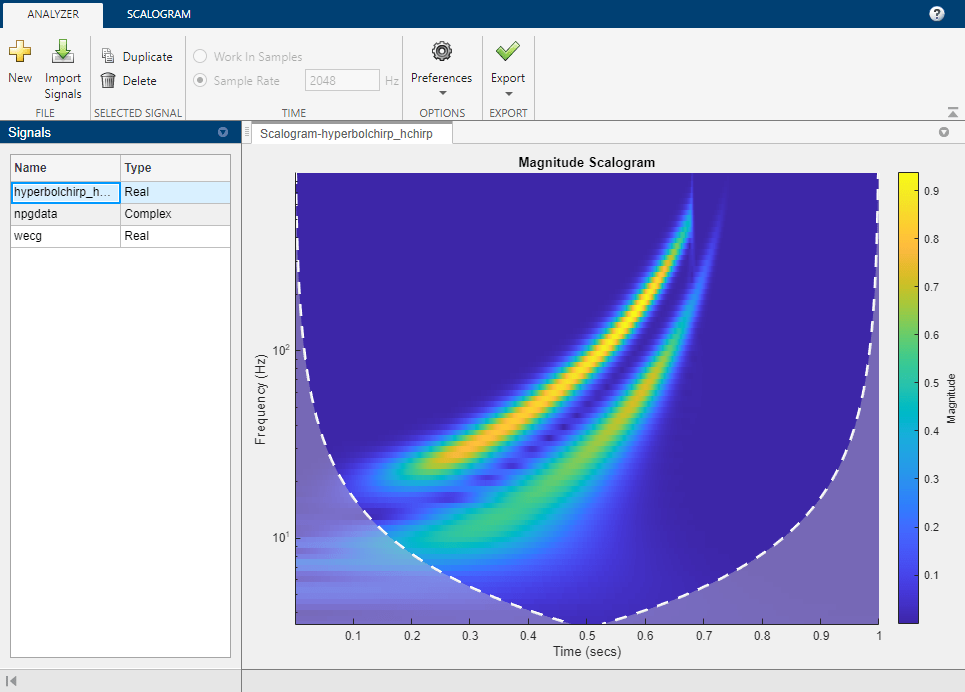
웨이블릿 시간-주파수 분석기 앱은 실수 값 1차원 신호와 복소수 값 1차원 신호의 스케일로그램 시각화를 위한 대화형 방식 툴입니다. 스케일로그램은 시간과 주파수의 함수로 플로팅된 연속 웨이블릿 변환(CWT)의 절댓값입니다. 주파수는 로그 스케일로 플로팅됩니다. 이 앱을 사용하여 다음을 수행할 수 있습니다.
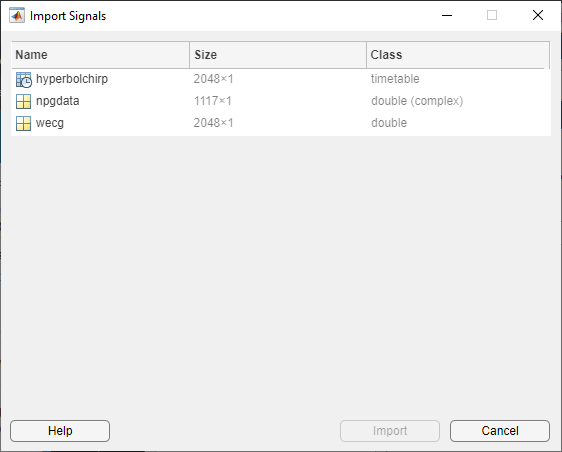
MATLAB® 작업 공간의 모든 1차원 신호에 액세스
동시에 여러 개의 신호 가져오기
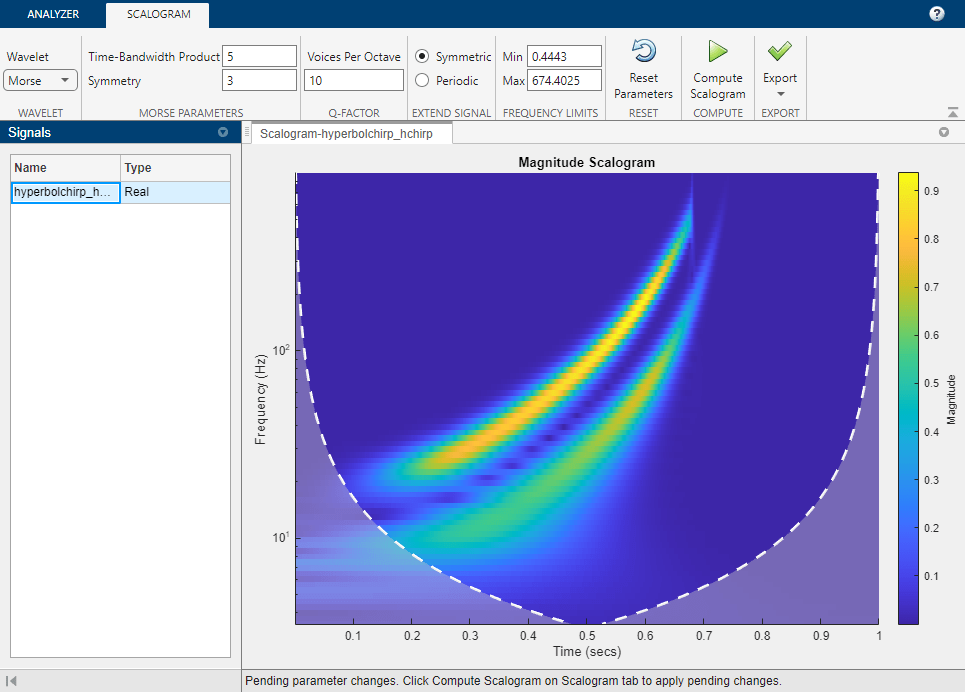
cwt를 사용하여 디폴트 파라미터 조정 및 스케일로그램 시각화원하는 해석적 웨이블릿 선택
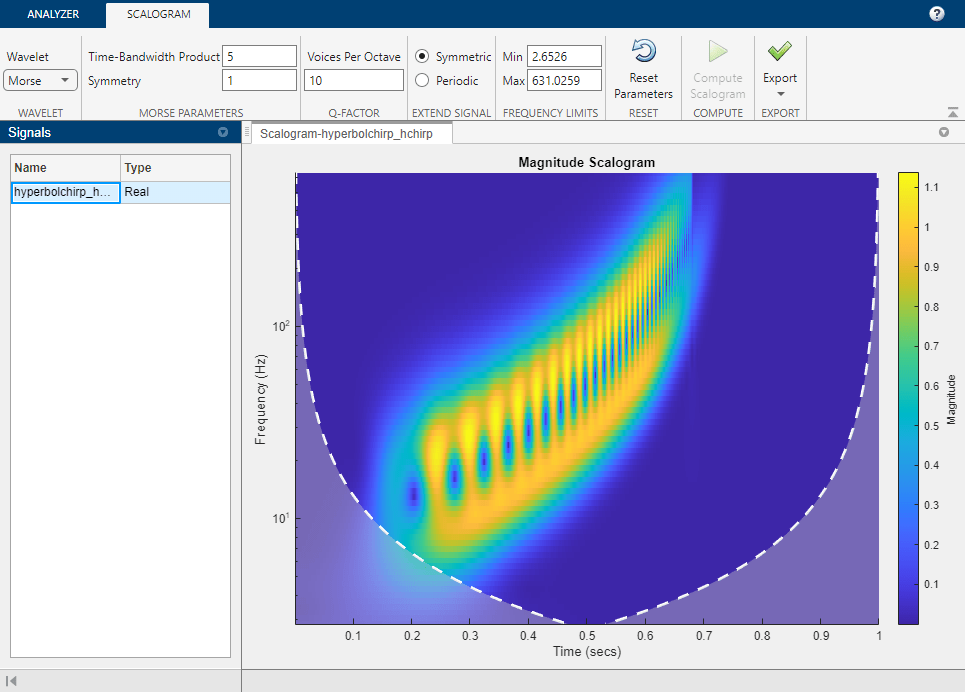
해석적 Morse 웨이블릿의 대칭성 및 시간-대역폭 파라미터 조정
작업 공간으로 CWT 내보내기
MATLAB 스크립트를 생성하여 작업 공간에 스케일로그램 재생성
여러 개의 신호 가져오기
자세한 내용은 Using Wavelet Time-Frequency Analyzer App 항목을 참조하십시오.
웨이블릿 시간-주파수 분석기 앱 열기
MATLAB 툴스트립: 앱 탭의 신호 처리 및 통신에서 앱 아이콘을 클릭합니다.
MATLAB 명령 프롬프트:
waveletTimeFrequencyAnalyzer를 입력합니다.
예제
디폴트 설정을 사용하여 스케일로그램 시각화하기
심전도 신호, 쌍곡 처프 신호, NPG2006 데이터셋 등 세 가지 1차원 신호를 MATLAB® 작업 공간으로 불러옵니다.
load wecg load hyperbolchirp load npg2006
npg2006 구조체형 배열에서 복소수 값 신호를 추출합니다.
npgdata = npg2006.cx; whos
Name Size Bytes Class Attributes hyperbolchirp 2048x1 33759 timetable npg2006 1x1 37184 struct npgdata 1117x1 17872 double complex wecg 2048x1 16384 double
웨이블릿 시간-주파수 분석기를 열고 신호 가져오기를 클릭합니다. 앱이 처리할 수 있는 모든 작업 공간 변수가 나열된 창이 표시됩니다.
모든 신호를 선택하고 가져오기를 클릭합니다. 짧은 일회성 초기화가 진행된 다음, 가져온 신호의 이름과 유형 정보로 신호 창이 채워집니다. hyperbolchirp의 경우 신호를 포함하는 타임테이블 변수의 이름이 타임테이블 이름 뒤에 추가됩니다(예: hyperbolchirp_hchirp). 강조 표시된 신호의 스케일로그램이 앱에 표시됩니다. 스케일로그램은 디폴트 설정이 적용된 cwt 함수를 사용하여 얻습니다. 가장자리 효과가 유의미해지는 위치를 나타내는 영향 원뿔(cone of influence)도 플로팅됩니다. 흰색 파선 밖의 회색 영역이 가장자리 효과가 유의미한 영역을 나타냅니다. 기본적으로 주파수의 단위는 주기/샘플입니다.
ECG 신호는 실수 값입니다. 신호 창에서 복소수 값 신호 npgdata를 선택합니다. 스케일로그램의 양의 성분과 음의 성분이 표시됩니다.
hyperbolchirp_hchirp를 선택합니다. 타임테이블에 시간 정보가 포함되므로 스케일로그램은 주파수(단위: 헤르츠)의 함수로 플로팅되고 타임테이블의 행 시간값을 시간 축의 기반으로 사용합니다. 비활성화된 샘플 레이트 필드는 행 시간값에서 결정된 샘플링 레이트를 표시합니다.
Morse 웨이블릿 파라미터 조정하기
쌍곡 처프 신호를 불러옵니다.
load hyperbolchirp웨이블릿 시간-주파수 분석기를 열고 신호를 앱으로 가져옵니다. 파라미터 설정에 액세스하려면 스케일로그램 탭을 클릭하십시오. 기본적으로 해석적 Morse (3, 60) 웨이블릿과 디폴트 설정이 적용된 cwt 함수를 사용하여 얻은 스케일로그램이 앱에 표시됩니다.
파라미터 재설정을 클릭하여 언제든지 CWT 파라미터를 디폴트 값으로 재설정할 수 있습니다. 파라미터를 재설정하면 스케일로그램 계산 버튼이 활성화됩니다.
(1,5) Morse 웨이블릿을 사용하여 스케일로그램을 시각화하기 위해 시간과 대역폭의 곱을 5로 설정합니다. 상태 표시줄에 보류 중인 변경 내용이 있음을 나타내는 텍스트가 표시됩니다. 이제 스케일로그램 계산 버튼이 활성화됩니다. 그 대신 처음에 대칭을 1로 설정했다면, 대칭 값이 1인 경우 대칭에 대한 시간과 대역폭의 곱의 비가 40을 초과하면 안 된다는 제약 조건을 위반하므로 앱에서 자동으로 값을 변경합니다. 자세한 내용은 팁 항목을 참조하십시오.
이제 대칭을 1로 설정하고 스케일로그램 계산을 클릭합니다. (1, 5) Morse 웨이블릿을 사용하여 얻은 스케일로그램이 앱에 표시됩니다.
(6, 50) Morse 웨이블릿을 사용하여 스케일로그램을 시각화하려면 먼저 시간과 대역폭의 곱을 50으로, 대칭을 6으로 설정한 다음 스케일로그램 계산을 클릭합니다.
스케일로그램 주파수 축 스케일 조정하기
신호 가져오기
쌍곡 처프 신호를 작업 공간으로 불러옵니다.
load hyperbolchirp스케일로그램 시각화하기
웨이블릿 시간-주파수 분석기를 열고 신호를 가져옵니다. 파라미터 설정에 액세스하려면 스케일로그램 탭을 클릭하십시오. 기본적으로 Morse (3,60) 웨이블릿과 디폴트 설정이 적용된 cwt 함수를 사용하여 얻은 스케일로그램이 앱에 표시됩니다. 신호가 타임테이블이므로 스케일로그램이 헤르츠 단위의 주파수 함수로 플로팅됩니다. 시간 축은 타임테이블의 행 시간값을 기반으로 합니다.
스케일로그램 탭에서 디폴트 설정을 조정합니다. Morse (5,20) 웨이블릿을 지정합니다. 옥타브당 26개의 음과 주기적 경계 확장을 사용하는 스케일로그램을 시각화합니다. 주파수가 로그 스케일로 플로팅됩니다.
스크립트 생성하기
스케일로그램에서 주파수 축 스케일을 조정하려면 먼저 웨이블릿 분석을 작업 공간에 다시 생성합니다.
스케일로그램을 작업 공간에 다시 생성하는 스크립트를 만듭니다. 내보내기 ▼ 메뉴에서 Generate MATLAB Script를 선택합니다. MATLAB® 편집기에 제목 없는 스크립트가 열립니다. 플롯에 영향 원뿔 경계선을 포함하기 위해 스크립트에서 cwt 함수 호출에 세 번째 출력 인수 coi를 추가합니다. 스크립트를 저장하고 실행합니다. 변수 scalogram과 frequency는 각각 스케일로그램과 주파수 벡터를 포함합니다.
%Parameters waveletParameters = [5,20]; voicesPerOctave = 26; extendSignal = false; %Compute cwt %Run the function call below without output arguments to plot the results [waveletTransform,frequency,coi] = cwt(hyperbolchirp,... WaveletParameters = waveletParameters,... VoicesPerOctave = voicesPerOctave,... ExtendSignal = extendSignal); scalogram = abs(waveletTransform);
올바른 시간 축을 사용하여 스케일로그램을 플로팅하기 위해 hyperbolchirp 타임테이블에서 행 시간값으로 구성된 벡터 Time을 추출합니다.
dataTimes = hyperbolchirp.Time;
주파수 축 조정하기 — 선형 스케일
pcolor 함수를 사용하여 스케일로그램을 플로팅합니다. 영향 원뿔 경계선을 포함합니다. 주파수는 선형 스케일로 플로팅됩니다.
pcolor(dataTimes,frequency,scalogram) shading flat title("Scalogram") xlabel("Time (s)") ylabel("Frequency (Hz)") hold on plot(dataTimes,coi,"w--",LineWidth=2) hold off colorbar
주파수 축 조정하기 — 로그 스케일
로그 스케일로 주파수를 플로팅하기 위해 현재 좌표축 핸들을 가져오고 YScale을 "log"로 설정합니다.
AX = gca;
set(AX,YScale="log")
MATLAB에서 로그 좌표축의 단위는 10의 거듭제곱(디케이드)입니다. 기본적으로 주파수 눈금은 최소 주파수와 최대 주파수 사이의 10의 거듭제곱이기 때문에 MATLAB은 1, 10, 100에 주파수 눈금을 배치합니다. 주파수 축 눈금을 추가하기 위해 frequency의 최소 주파수와 최대 주파수를 가져옵니다. 최소 주파수와 최대 주파수 사이의 로그 간격 주파수 집합을 만듭니다. cwt는 높은 주파수에서 낮은 주파수 순서로 주파수를 반환합니다.
minf = frequency(end); maxf = frequency(1); numfreq = 10; freq = logspace(log10(minf),log10(maxf),numfreq);
주파수 축 눈금과 레이블을 새로운 주파수로 교체합니다.
AX.YTickLabelMode = "auto";
AX.YTick = freq;
CWT에서 주파수는 2의 거듭제곱으로 계산됩니다. 주파수 눈금과 눈금 레이블을 2의 거듭제곱 단위로 만듭니다.
freq = 2.^(round(log2(minf)):round(log2(maxf)));
AX.YTickLabelMode = "auto";
AX.YTick = freq;
관련 예제
파라미터
프로그래밍 방식으로 사용
제한 사항
작업 공간에 스케일로그램을 만들기 위해 생성한 MATLAB 스크립트는 신호 창에 선택된 신호 이름을 사용합니다. 변수가 MATLAB 작업 공간에 존재하지 않으면 스크립트에서 오류가 발생합니다. 오류가 발생하면 스크립트의 변수 이름을 원본 신호 이름으로 바꾸거나 작업 공간에 변수를 만드십시오.
웨이블릿 시간-주파수 분석기 앱의 인스턴스는 MATLAB 세션에서 하나만 실행할 수 있습니다.
팁
Morse 웨이블릿 파라미터인 시간과 대역폭의 곱과 대칭은 다음 세 가지 제약 조건을 충족해야 합니다.
대칭, 즉 감마는 1보다 크거나 같아야 합니다.
시간과 대역폭의 곱은 대칭보다 크거나 같아야 합니다.
대칭에 대한 시간과 대역폭의 곱의 비는 40을 초과할 수 없습니다.
유효하지 않은 설정으로 스케일로그램 시각화를 시도하지 않도록, 앱은 사용자가 변경하는 모든 파라미터를 검증합니다. 제약 조건에 위반되는 값을 입력하면 앱에서 자동으로 유효한 값으로 교체합니다. 그렇게 교체된 새로운 값이 원하는 값과 다를 수 있습니다. 예기치 않은 결과를 피하려면 입력값으로 구성한 설정이 유효한지 항상 확인해야 합니다. 자세한 내용은 Morse 웨이블릿 파라미터 조정하기 예제를 참조하십시오.
버전 내역
R2022a에 개발됨
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)