plotResiduals
Class: GeneralizedLinearMixedModel
Plot residuals of generalized linear mixed-effects model
Syntax
Description
plotResiduals(
specifies the type of residuals to plot.glme,plottype,ResidualType=residualtype)
h = plotResiduals(___)h, to the lines or patches in the plot
of residuals.
Input Arguments
Generalized linear mixed-effects model, specified as a GeneralizedLinearMixedModel object.
For properties and methods of this object, see GeneralizedLinearMixedModel.
Type of residual plot, specified as one of the following.
| Value | Description |
|---|---|
"histogram" | Histogram of residuals |
"caseorder" | Residuals versus case order. Case order is the same as the
row order used in the input data tbl when fitting
the model using fitglme. |
"fitted" | Residuals versus fitted values |
"lagged" | Residuals versus lagged residual (r(t) versus r(t – 1)) |
"probability" | Normal probability plot |
"observed" | Observed vs. fitted values. This plot includes a dotted reference line of y = x. Each residual is represented by the vertical distance from the corresponding observed value to the reference line. |
"symmetry" | Symmetry plot |
Example: plotResiduals(glme,"lagged")
Since R2024a
Target axes, specified as an Axes object. If you do not specify the axes,
then plotResiduals uses the current axes (gca).
Residual type, specified by one of the following.
| Residual Type | Formula |
|---|---|
"raw" |
|
"Pearson" |
|
In each of these equations:
yi is the ith element of the n-by-1 response vector, y, where i = 1, ..., n.
g-1 is the inverse link function for the model.
xiT is the ith row of the fixed-effects design matrix X.
ziT is the ith row of the random-effects design matrix Z.
δi is the ith offset value.
σ2 is the dispersion parameter.
wi is the ith observation weight.
vi is the variance term for the ith observation.
μi is the mean of the response for the ith observation.
and are estimated values of β and b.
Raw residuals from a generalized linear mixed-effects model have nonconstant variance. Pearson residuals are expected to have an approximately constant variance, and are generally used for analysis.
Example: ResidualType="Pearson"
Output Arguments
Handle to the residual plot, returned as a graphics object. You can use dot notation to change certain property values of the object, including face color for a histogram, and marker style and color for a scatterplot. For more information, see Access Property Values.
Examples
Load the sample data.
load mfrThis simulated data is from a manufacturing company that operates 50 factories across the world, with each factory running a batch process to create a finished product. The company wants to decrease the number of defects in each batch, so it developed a new manufacturing process. To test the effectiveness of the new process, the company selected 20 of its factories at random to participate in an experiment: Ten factories implemented the new process, while the other ten continued to run the old process. In each of the 20 factories, the company ran five batches (for a total of 100 batches) and recorded the following data:
Flag to indicate whether the batch used the new process (
newprocess)Processing time for each batch, in hours (
time)Temperature of the batch, in degrees Celsius (
temp)Categorical variable indicating the supplier (
A,B, orC) of the chemical used in the batch (supplier)Number of defects in the batch (
defects)
The data also includes time_dev and temp_dev, which represent the absolute deviation of time and temperature, respectively, from the process standard of 3 hours at 20 degrees Celsius.
Fit a generalized linear mixed-effects model using newprocess, time_dev, temp_dev, and supplier as fixed-effects predictors. Include a random-effects term for intercept grouped by factory, to account for quality differences that might exist due to factory-specific variations. The response variable defects has a Poisson distribution, and the appropriate link function for this model is log. Use the Laplace fit method to estimate the coefficients. Specify the dummy variable encoding as 'effects', so the dummy variable coefficients sum to 0.
The number of defects can be modeled using a Poisson distribution:
This corresponds to the generalized linear mixed-effects model
where
is the number of defects observed in the batch produced by factory during batch .
is the mean number of defects corresponding to factory (where ) during batch (where ).
, , and are the measurements for each variable that correspond to factory during batch . For example, indicates whether the batch produced by factory during batch used the new process.
and are dummy variables that use effects (sum-to-zero) coding to indicate whether company
CorB, respectively, supplied the process chemicals for the batch produced by factory during batch .is a random-effects intercept for each factory that accounts for factory-specific variation in quality.
glme = fitglme(mfr,'defects ~ 1 + newprocess + time_dev + temp_dev + supplier + (1|factory)','Distribution','Poisson','Link','log','FitMethod','Laplace','DummyVarCoding','effects');
Create diagnostic plots using Pearson residuals to test the model assumptions.
Plot a histogram to visually confirm that the mean of the Pearson residuals is equal to 0. If the model is correct, we expect the Pearson residuals to be centered at 0.
plotResiduals(glme,'histogram','ResidualType','Pearson')

The histogram shows that the Pearson residuals are centered at 0.
Plot the Pearson residuals versus the fitted values, to check for signs of nonconstant variance among the residuals (heteroscedasticity). We expect the conditional Pearson residuals to have a constant variance. Therefore, a plot of conditional Pearson residuals versus conditional fitted values should not reveal any systematic dependence on the conditional fitted values.
plotResiduals(glme,'fitted','ResidualType','Pearson')

The plot does not show a systematic dependence on the fitted values, so there are no signs of nonconstant variance among the residuals.
Plot the Pearson residuals versus lagged residuals, to check for correlation among the residuals. The conditional independence assumption in GLME implies that the conditional Pearson residuals are approximately uncorrelated.
plotResiduals(glme,'lagged','ResidualType','Pearson')
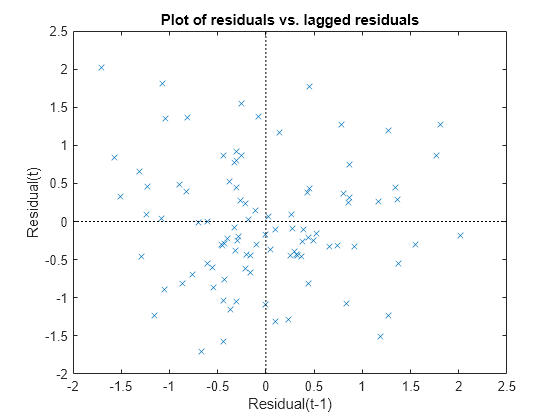
There is no pattern to the plot, so there are no signs of correlation among the residuals.
Version History
You can now plot observed versus fitted values by specifying the
plottype input argument as
"observed".
Specify the target axes for the plot by using the ax input
argument.
See Also
GeneralizedLinearMixedModel | fitglme | fitted | plot | residuals
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)