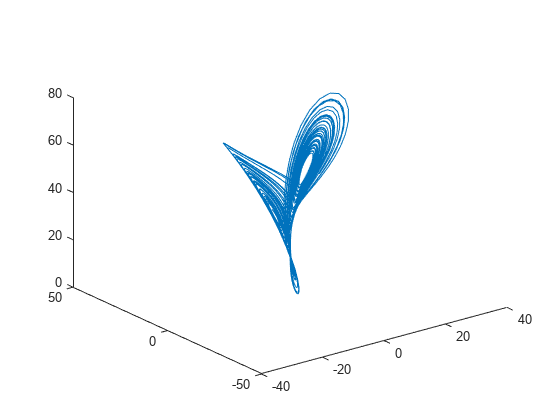
lyapunovExponent

무한히 가까운 궤적의 분리율 특성화

구문

lyapExp = lyapunovExponent(X,fs)

lyapExp = lyapunovExponent(X,fs,lag)

lyapExp = lyapunovExponent(X,fs,[],dim)

lyapExp = lyapunovExponent(X,fs,lag,dim)

[lyapExp,estep,ldiv] = lyapunovExponent(___)

___ = lyapunovExponent(___,Name,Value)

lyapunovExponent(___)

설명

lyapExp = lyapunovExponent(X,fs)는 샘플링 주파수 fs를 사용하여 균일하게 샘플링된 시간 영역 신호 X의 랴푸노프 지수를 추정합니다. lyapunovExponent를 사용해 위상 공간에서 무한히 가까운 궤적의 분리율을 특성화하여 서로 다른 끌개를 구분합니다. 랴푸노프 지수는 시스템의 무질서 수준을 수량화하는 데 유용하며, 결과적으로 잠재적인 결함을 검출하는 데 사용할 수 있습니다.

lyapExp = lyapunovExponent(X,fs,lag)는 시간 지연 lag에 대한 랴푸노프 지수를 추정합니다.

lyapExp = lyapunovExponent(X,fs,[],dim)은 임베딩 차원 dim에 대한 랴푸노프 지수를 추정합니다.

lyapExp = lyapunovExponent(X,fs,lag,dim)은 시간 지연 lag와 임베딩 차원 dim에 대한 랴푸노프 지수를 추정합니다.

[lyapExp,estep,ldiv] = lyapunovExponent(___)는 균일하게 샘플링된 시간 영역 신호 X의 랴푸노프 지수, 확장 스텝 및 해당하는 로그 발산을 추정합니다. 신호 진단을 위해 확장 스텝 estep 및 해당하는 로그 발산 ldiv를 사용합니다.

___ = lyapunovExponent(___,Name,Value)는 하나 이상의 Name,Value 쌍의 인수로 지정된 추가 옵션을 사용하여 랴푸노프 지수를 추정합니다.

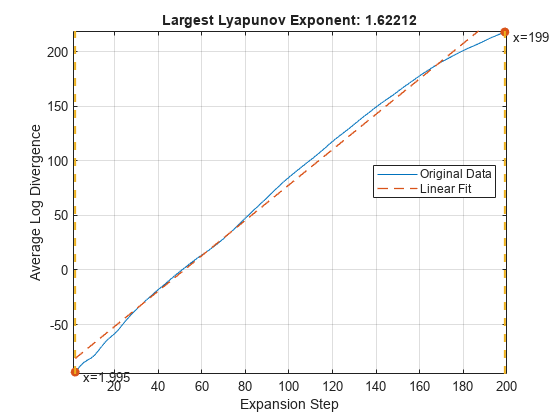
lyapunovExponent(___)(출력 인수 없음)는 확장 스텝에 대한 평균 로그 발산 플롯을 만듭니다.

생성된 대화형 방식 플롯을 사용하여 적절한 ExpansionRange를 찾습니다.

예제

가장 큰 랴푸노프 지수 시각화 및 추정하기

이 예제에서는 무질서한 해의 고유한 집합을 설명하는 로렌츠 끌개(Lorenz attractor)가 있다고 가정합니다.

데이터 세트와 샘플링 주파수 fs를 작업 공간으로 불러오고 로렌츠 끌개를 3차원으로 시각화합니다.

load('lorenzAttractorExampleData.mat','data','fs');
plot3(data(:,1),data(:,2),data(:,3));

이 예제에서는 로렌츠 끌개의 x 방향 데이터를 사용합니다. Lag를 알 수 없으므로 phaseSpaceReconstruction을 사용하여 지연을 추정합니다. 로렌츠 끌개는 3차원 시스템이므로 차원을 3으로 설정합니다. dim 및 lag 파라미터는 확장 스텝에 대한 로그 발산 플롯을 만드는 데 필요합니다.

xdata = data(:,1);
dim = 3;
[~,lag] = phaseSpaceReconstruction(xdata,[],dim)

lag = 10

이전 단계에서 얻은 lag 값을 사용하여 로렌츠 끌개에 대해 확장 스텝에 대한 평균 로그 발산 플롯을 만듭니다. 모든 확장 스텝을 캡처할 수 있도록 충분히 큰 확장 범위를 설정합니다.

eRange = 200;
lyapunovExponent(xdata,fs,lag,dim,'ExpansionRange',eRange)

첫 번째 녹색 세로 파선(왼쪽)은 확장 범위를 추정하는 데 사용되는 최소 스텝 수를 나타내고, 두 번째 녹색 세로 파선(오른쪽)은 사용되는 최대 스텝 수를 나타냅니다. 첫 번째 세로선과 두 번째 세로선이 함께 확장 범위를 나타냅니다. 빨간색 파선은 확장 범위 내에서 데이터에 대한 선형 피팅 선을 나타냅니다.

가장 큰 랴푸노프 지수를 계산하려면 먼저 정확한 추정에 필요한 확장 범위를 확인해야 합니다.

플롯에서 두 개의 녹색 세로 파선을 끌어서 놓아 선형 피팅 선을 원래 데이터 선에 최적으로 맞춰 확장 범위 ${\mathit{K}}_{\min }$ 및 ${\mathit{K}}_{\max }$를 얻습니다.

적절한 피팅을 위해 두 개의 세로선을 끌어서 놓은 후 확장 범위의 새 값을 확인합니다.

확장 범위는 정수만 사용하여 지정할 수 있으므로 ${\mathit{K}}_{\min }$과 ${\mathit{K}}_{\max }$를 가장 가까운 정수로 반올림합니다. 새 확장 범위 값을 사용하여 로렌츠 끌개의 가장 큰 랴푸노프 지수를 구합니다.

Kmin = 21;
Kmax = 161;
lyapExp = lyapunovExponent(xdata,fs,lag,dim,'ExpansionRange',[Kmin Kmax])

lyapExp = 1.6834

랴푸노프 지수가 음수이면 수렴을 나타내는 반면, 랴푸노프 지수가 양수이면 발산과 무질서를 나타냅니다. lyapExp의 크기는 무한히 가까운 궤적의 수렴률 또는 발산율을 나타내는 지표입니다.

입력 인수

X — 균일하게 샘플링된 시간 영역 신호

벡터 | 배열 | 타임테이블

균일하게 샘플링된 시간 영역 신호로, 벡터, 배열 또는 타임테이블로 지정됩니다. X에 여러 개의 열이 있는 경우 lyapunovExponent는 X를 다변량 신호로 처리하여 가장 큰 랴푸노프 지수를 계산합니다.

X가 행 벡터로 지정된 경우 lyapunovExponent는 X를 일변량 신호로 처리합니다.

fs — 샘플링 주파수

스칼라

샘플링 주파수로, 스칼라로 지정됩니다. 샘플링 주파수 또는 샘플링 레이트는 1초 동안 얻은 평균 샘플 수입니다.

fs를 제공하지 않으면 랴푸노프 지수를 계산하는 데 정규화 주파수 2π가 사용됩니다. X가 타임테이블로 지정된 경우 이 인수에서 샘플링 시간이 유추됩니다.

dim — 임베딩 차원

스칼라 | 벡터

임베딩 차원으로, 스칼라 또는 벡터로 지정됩니다. dim은 'Dimension' 이름-값 쌍과 동일합니다.

lag — 시간 지연

스칼라 | 벡터

시간 지연으로, 스칼라 또는 벡터로 지정됩니다. lag는 'Lag' 이름-값 쌍과 동일합니다.

이름-값 인수

선택적 인수 쌍을 Name1=Value1,...,NameN=ValueN으로 지정합니다. 여기서 Name은 인수 이름이고 Value는 대응값입니다. 이름-값 인수는 다른 인수 뒤에 와야 하지만, 인수 쌍의 순서는 상관없습니다.

R2021a 이전 릴리스에서는 쉼표를 사용하여 각 이름과 값을 구분하고 Name을 따옴표로 묶으십시오.

예: …,'Dimension',3

Dimension — 임베딩 차원

2 (디폴트 값) | 스칼라 | 벡터

임베딩 차원으로, 'Dimension'과 함께 스칼라 또는 벡터가 쉼표로 구분되어 지정됩니다. Dimension이 스칼라인 경우 X의 모든 열은 Dimension을 사용하여 재구성됩니다. Dimension이 X의 열 개수와 동일한 길이를 가진 벡터인 경우 열 i의 재구성 차원은 Dimension(i)입니다.

시스템의 차원, 즉 상태 개수에 따라 Dimension을 지정합니다. 임베딩 차원에 대한 자세한 내용은 phaseSpaceReconstruction 항목을 참조하십시오.

Lag — 위상 공간 재구성의 지연

1 (디폴트 값) | 스칼라 | 벡터

위상 공간 재구성의 지연으로, 'Lag'와 함께 스칼라 또는 벡터가 쉼표로 구분되어 지정됩니다. Lag가 스칼라인 경우 X의 모든 열은 Lag를 사용하여 재구성됩니다. Lag가 X의 열 개수와 동일한 길이를 가진 벡터인 경우 열 i의 재구성 지연은 Lag(i)입니다.

Lag의 디폴트 값은 1입니다.

지연 값이 너무 작으면 데이터에 랜덤 잡음이 발생합니다. 반대로, 지연 값이 너무 크면 재구성된 동특성이 시계열의 실제 동특성을 나타내지 않습니다. 최적의 지연을 추정하는 방법에 대한 자세한 내용은 phaseSpaceReconstruction 항목을 참조하십시오.

MinSeparation — 평균 주기

ceil(fs/max(meanfreq(X,fs))) (디폴트 값) | 양의 정수 스칼라

평균 주기로, 'MinSeparation'과 함께 양의 정수 스칼라가 쉼표로 구분되어 지정됩니다.

MinSeparation은 점 i의 최근접이웃 i^*를 찾아서 가장 큰 랴푸노프 지수를 추정하는 데 사용되는 임계값입니다.

MinSeparation의 디폴트 값은 ceil(fs/max(meanfreq(X,fs)))입니다.

ExpansionRange — 확장 스텝의 범위

[1, 5] (디폴트 값) | 1x2 양의 정수형 배열 | 양의 정수 스칼라

확장 스텝의 범위로, 'ExpansionRange'와 함께 1x2 양의 정수형 배열 또는 양의 정수 스칼라가 쉼표로 구분되어 지정됩니다.

ExpansionRate의 최솟값과 최댓값은 랴푸노프 지수를 계산하기 위한 국소 확장률을 추정하는 데 사용됩니다.

ExpansionRange가 스칼라 M으로 지정된 경우 범위는 [1, M]으로 설정됩니다. ExpansionRange는 양의 정수를 사용해서만 지정할 수 있으며 디폴트 값은 [1, 5]입니다.

출력 인수

lyapExp — 가장 큰 랴푸노프 지수

스칼라

가장 큰 랴푸노프 지수로, 스칼라로 반환됩니다. lyapExp는 위상 공간에서 가까운 궤적의 발산율 또는 수렴률을 수량화합니다.

랴푸노프 지수가 음수이면 수렴을 나타내는 반면, 랴푸노프 지수가 양수이면 발산과 무질서를 나타냅니다. lyapExp의 크기는 무한히 가까운 궤적의 수렴률 또는 발산율을 나타내는 지표입니다.

데이터 세트 내의 발산 수준을 식별하는 기능은 진동 및 음향 신호를 연구하여 부품의 고장을 추정하거나 선박 운동에 기반하여 선박이 언제 전복될지 예측하는 엔지니어링 분야에서 유용합니다.[2][3]

estep — 추정에 사용되는 확장 스텝

배열

추정에 사용되는 확장 스텝으로, 배열로 반환됩니다. estep은 확장 범위의 최댓값 및 최솟값 간의 차이를 ExpansionRange의 최댓값으로 정의된 점의 개수로 균일하게 분할한 값입니다.

ldiv — 로그 발산

배열

로그 발산으로, estep과 크기가 같은 배열로 반환됩니다. ldiv에 있는 각 값의 크기는 estep에 있는 각 점의 로그 수렴 또는 로그 발산에 해당합니다.

알고리즘

랴푸노프 지수는 다음과 같은 방법으로 계산됩니다.

1. lyapunovExponent 함수가 먼저 임베딩 차원 m과 지연 τ를 사용하여, 지연된 재구성 Y_1:N을 생성합니다.

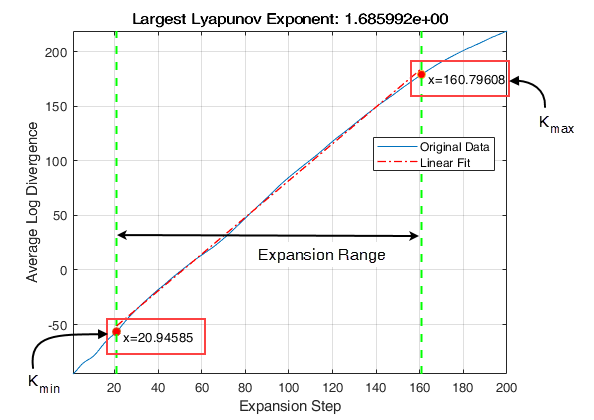
2. 그런 다음 소프트웨어에서 점 i에 대해 $$\underset{i^{*}}{\min }\Vert Y_i-Y_{i^{*}}\Vert$$를 충족하는 최근접이웃 점 i^*를 찾습니다. 이 때, $$\left|i-i^{*}\right|>MinSeparation$$이며, 평균 주기인 MinSeparation은 평균 주파수의 역수입니다.

3. [1]에서, 전체 확장 범위에 대한 랴푸노프 지수는 다음과 같이 계산됩니다.

   $$\lambda (i)=\frac{1}{\left(K_{\max }-K_{\min }+1\right)dt}{\displaystyle \sum _{K=K_{\min }}^{K_{\max }}\frac{1}{K}\ln \frac{\Vert Y_{i+K}-Y_{i^{*}+K}\Vert }{\Vert Y_i-Y_{i^{*}}\Vert }}$$

   여기서 K_min과 K_max는 ExpansionRange를 나타내고 dt는 샘플링 시간이며 $$ldiv=\ln \frac{\Vert Y_{i+K}-Y_{i^{*}+K}\Vert }{\Vert Y_i-Y_{i^{*}}\Vert }$$입니다.

4. 그런 다음 위 단계에서 계산된 랴푸노프 지수에 대한 단일 값을 다음 polyfit 명령을 사용하여 계산합니다.

   $$lyapExp\text{ = }polyfit\left(\left[K_{\min }{K}_{\max }\right],\lambda (i)\right)$$

참고 문헌

[1] Michael T. Rosenstein , James J. Collins , Carlo J. De Luca. "A practical method for calculating largest Lyapunov exponents from small data sets ". Physica D 1993. Volume 65. Pages 117-134.

[2] Caesarendra, Wahyu & Kosasih, P & Tieu, Kiet & Moodie, Craig. "An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis." IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013.1713-1718. 10.1109/AIM.2013.6584344.

[3] McCue, Leigh & W. Troesch, Armin. (2011). "Use of Lyapunov Exponents to Predict Chaotic Vessel Motions". Fluid Mechanics and its Applications. 97. 415-432. 10.1007/978-94-007-1482-3_23.

확장 기능

C/C++ 코드 생성

MATLAB® Coder™를 사용하여 C 코드나 C++ 코드를 생성할 수 있습니다.

사용법 관련 참고 및 제한 사항:

• 플롯을 생성하는 구문은 코드 생성 시 지원되지 않습니다.

버전 내역

R2018a에 개발됨

참고 항목

approximateEntropy | correlationDimension | phaseSpaceReconstruction