Pressure Relief Valve (G)
Pressure relief valve in a gas network
Libraries:
Simscape /
Fluids /
Gas /
Valves & Orifices /
Pressure Control Valves
Description
The Pressure Relief Valve (G) block represents an orifice that opens with inlet pressure to keep the pressure from reaching extreme levels. At normal pressures, the valve is closed and only releases leakage flow. Above a specified pressure setting, the valve begins to open, which allows the gas to vent from the region of high pressure. The opening area increases with inlet pressure up to a maximum value, at which point the valve is fully open and pressure rises unabated.
The valve responds to inlet pressure relative to the outlet or inlet pressure relative to the environment. The chosen pressure measurement is the control pressure of the valve. The Control pressure specification parameter determines which of the measurements the block uses during simulation.
The relationship between the opening area and the pressure drop depends on the parameterization of the valve. That relationship can take the form of a linear analytical expression or a tabulated function.
The flow can be laminar or turbulent, and it can reach up to sonic speeds. The maximum velocity happens at the throat of the valve where the flow is narrowest and fastest. The flow chokes and the velocity saturates when a drop in downstream pressure can no longer increase the velocity. Choking occurs when the back-pressure ratio reaches the critical value characteristic of the valve. The block does not capture supersonic flow.
Valve Opening Fraction
The inlet pressure is the valve control signal. The more the inlet pressure rises over the
pressure setting of the valve, the greater the opening area becomes. The amount that
the control pressure exceeds the pressure setting determines how much the valve
opens. When the Opening characteristic parameter is
Linear, the block calculates the valve opening
fraction to scale the flow characteristic parameters. The normalized control
pressure is
where:
PCtl is the control pressure.
When Opening pressure specification is
Pressure difference of port A relative to port B,where PA is the absolute pressure at port A and PB is the absolute pressure at port B.
When Opening pressure specification is
Gauge pressure at port A,where PAtm is the atmospheric pressure specified in the Gas Properties (G) block of the model.
PSet is the set pressure.
When Opening pressure specification is
Pressure difference of port A relative to port B, PSet, is the value of the Set pressure differential parameterWhen Opening pressure specification is
Gauge pressure at port A, PSet is the value of the Set pressure (gauge) parameterΔP is the value of the Pressure regulation range parameter.
The fraction of valve opening, L, is
where Lleak is the value of the Leakage flow fraction parameter.
When the Opening characteristic parameter is
Linear and the Smoothing
factor parameter is nonzero, the block applies numerical
smoothing to the normalized control pressure, . Enabling smoothing helps maintain numerical robustness in
your simulation.
For more information, see Numerical Smoothing.
Valve Parameterizations
The block behavior depends on the Valve parametrization parameter:
Cv flow coefficient— The flow coefficient Cv determines the block parameterization. The flow coefficient measures the ease with which a gas can flow when driven by a certain pressure differential.Kv flow coefficient— The flow coefficient Kv, where , determines the block parameterization. The flow coefficient measures the ease with which a gas can flow when driven by a certain pressure differential.Sonic conductance— The sonic conductance of the resistive element at steady state determines the block parameterization. The sonic conductance measures the ease with which a gas can flow when choked, which is a condition in which the flow velocity is at the local speed of sound. Choking occurs when the ratio between downstream and upstream pressures reaches a critical value known as the critical pressure ratio.Orifice area— The size of the flow restriction determines the block parametrization.
Opening Characteristics
The flow characteristic relates the opening of the valve to the input that produces it. The opening is expressed as a sonic conductance, flow coefficient, or restriction area, determined by the Valve parameterization parameter.
The flow characteristic is normally given at steady state, with the inlet at a constant, carefully controlled pressure. The flow characteristic depends only on the valve and can be linear or nonlinear. To capture the flow characteristics, use the Opening characteristic parameter:
Linear— The measure of flow capacity is a linear function of the valve opening fraction. As the opening fraction rises from0to1, the measure of flow capacity scales from the specified minimum to the specified maximum.
Tabulated— The measure of flow capacity is a general function, which can be linear or nonlinear, of the orifice opening fraction. The function is specified in tabulated form, with the independent variable specified by the Opening pressure differential vector or the Opening pressure (gauge) vector.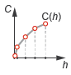
Momentum Balance
The block equations depend on the Orifice parametrization parameter.
When you set Orifice parametrization to Cv
flow coefficient parameterization, the mass flow rate, , is
where:
Cv is the flow coefficient.
N6 is a constant equal to 27.3 for mass flow rate in kg/hr, pressure in bar, and density in kg/m3.
Y is the expansion factor.
pin is the inlet pressure.
pout is the outlet pressure.
ρin is the inlet density.
The expansion factor is
where:
Fγ is the ratio of the isentropic exponent to 1.4.
xT is the value of the xT pressure differential ratio factor at choked flow parameter.
The block smoothly transitions to a linearized form of the equation when the pressure ratio, , rises above the value of the Laminar flow pressure ratio parameter, Blam,
where:
When the pressure ratio, , falls below , the orifice becomes choked and the block switches to the equation
When you set Orifice parametrization to Kv flow
coefficient parameterization, the block uses these same
equations, but replaces Cv with
Kv by using the relation . For more information on the mass flow equations when the
Orifice parametrization parameter is Kv
flow coefficient parameterization or Cv flow
coefficient parameterization, see [2][3].
When you set Orifice parametrization to
Sonic conductance parameterization, the mass flow
rate, , is
where:
C is the sonic conductance.
Bcrit is the critical pressure ratio.
m is the value of the Subsonic index parameter.
Tref is the value of the ISO reference temperature parameter.
ρref is the value of the ISO reference density parameter.
Tin is the inlet temperature.
The block smoothly transitions to a linearized form of the equation when the pressure ratio, , rises above the value of the Laminar flow pressure ratio parameter Blam,
When the pressure ratio, , falls below the critical pressure ratio, Bcrit, the orifice becomes choked and the block switches to the equation
The Sonic conductance setting of the
Valve parameterization parameter is for pneumatic
applications. If you use this setting for gases other than air, you may need to
scale the sonic conductance by the square root of the specific gravity.
For more information on the mass flow equations when the Orifice
parametrization parameter is Sonic conductance
parameterization, see [1].
When you set Orifice parametrization to
Orifice area parameterization, the mass flow
rate, , is
where:
Sr is the orifice or valve area.
S is the value of the Cross-sectional area at ports A and B parameter.
Cd is the value of the Discharge coefficient parameter.
γ is the isentropic exponent.
The block smoothly transitions to a linearized form of the equation when the pressure ratio, , rises above the value of the Laminar flow pressure ratio parameter, Blam,
When the pressure ratio, , falls below , the orifice becomes choked and the block switches to the equation
For more information on the mass flow equations when the Orifice
parametrization parameter is Orifice area
parameterization, see [4].
Mass Balance
The block assumes the volume and mass of fluid inside the valve is very small and ignores these values. As a result, no amount of fluid can accumulate in the valve. By the principle of conservation of mass, the mass flow rate into the valve through one port equals that out of the valve through the other port
where is defined as the mass flow rate into the valve through the port indicated by the A or B subscript.
Energy Balance
The resistive element of the block is an adiabatic component. No heat exchange can occur between the fluid and the wall that surrounds it. No work is done on or by the fluid as it traverses from inlet to outlet. Energy can flow only by advection, through ports A and B. By the principle of conservation of energy, the sum of the port energy flows is always equal to zero
where ϕ is the energy flow rate into the valve through ports A or B.
Assumptions and Limitations
The equation for the
Orifice areaparameterization is less accurate for gases that are far from ideal.This block does not model supersonic flow.
Ports
Conserving
Parameters
References
[1] ISO 6358-3. "Pneumatic fluid power – Determination of flow-rate characteristics of components using compressible fluids – Part 3: Method for calculating steady-state flow rate characteristics of systems". 2014.
[2] IEC 60534-2-3. "Industrial-process control valves – Part 2-3: Flow capacity – Test procedures". 2015.
[3] ANSI/ISA-75.01.01. "Industrial-Process Control Valves – Part 2-1: Flow capacity – Sizing equations for fluid flow underinstalled conditions". 2012.
[4] P. Beater. Pneumatic Drives. Springer-Verlag Berlin Heidelberg. 2007.