forecast

Forecast univariate autoregressive integrated moving average (ARIMA) model responses or conditional variances

Syntax

[Y,YMSE] = forecast(Mdl,numperiods,Y0)

[Y,YMSE] = forecast(Mdl,numperiods,Y0,Name,Value)

[Y,YMSE,V] = forecast(___)

Description

[Y,YMSE] = forecast(Mdl,numperiods,Y0) returns numperiods consecutive forecasted responses Y and corresponding mean square errors (MSE) YMSE of the fully specified, univariate ARIMA model Mdl. The presample response data Y0 initializes the model to generate forecasts.

[Y,YMSE] = forecast(Mdl,numperiods,Y0,Name,Value) uses additional options specified by one or more name-value arguments. For example, for a model with a regression component (that is, an ARIMAX model), 'X0',X0,'XF',XF specifies the presample and forecasted predictor data X0 and XF, respectively.

[Y,YMSE,V] = forecast(___) also forecasts numperiods conditional variances V of a composite conditional mean and variance model (for example, an ARIMA and GARCH composite model) using any of the input argument combinations in the previous syntaxes.

Examples

Forecast Conditional Mean Response

Forecast the conditional mean response of simulated data over a 30-period horizon.

Simulate 130 observations from a multiplicative seasonal moving average (MA) model with known parameter values.

Mdl = arima('MA',{0.5,-0.3},'SMA',0.4,'SMALags',12,...
		'Constant',0.04,'Variance',0.2);
rng(200);
Y = simulate(Mdl,130);

Fit a seasonal MA model to the first 100 observations, and reserve the remaining 30 observations to evaluate forecast performance.

MdlTemplate = arima('MALags',1:2,'SMALags',12);
EstMdl = estimate(MdlTemplate,Y(1:100));

 
    ARIMA(0,0,2) Model with Seasonal MA(12) (Gaussian Distribution):
 
                 Value      StandardError    TStatistic      PValue  
                ________    _____________    __________    __________

    Constant     0.20403      0.069064         2.9542       0.0031344
    MA{1}        0.50212      0.097298         5.1606      2.4619e-07
    MA{2}       -0.20174       0.10447        -1.9312        0.053464
    SMA{12}      0.27028       0.10907          2.478        0.013211
    Variance     0.18681      0.032732         5.7073       1.148e-08

EstMdl is a new arima model that contains estimated parameters (that is, a fully specified model).

Forecast the fitted model into a 30-period horizon. Specify the estimation period data as a presample.

[YF,YMSE] = forecast(EstMdl,30,Y(1:100));

YF(15)

ans = 0.2040

YMSE(15)

ans = 0.2592

YF is a 30-by-1 vector of forecasted responses, and YMSE is a 30-by-1 vector of corresponding MSEs. The 15-period-ahead forecast is 0.2040 and its MSE is 0.2592.

Visually compare the forecasts to the holdout data.

figure
h1 = plot(Y,'Color',[.7,.7,.7]);
hold on
h2 = plot(101:130,YF,'b','LineWidth',2);
h3 = plot(101:130,YF + 1.96*sqrt(YMSE),'r:',...
		'LineWidth',2);
plot(101:130,YF - 1.96*sqrt(YMSE),'r:','LineWidth',2);
legend([h1 h2 h3],'Observed','Forecast',...
		'95% Confidence Interval','Location','NorthWest');
title(['30-Period Forecasts and Approximate 95% '...
			'Confidence Intervals'])
hold off

Forecast NASDAQ Composite Index

Forecast the daily NASDAQ Composite Index over a 500-day horizon.

Load the NASDAQ data set, and extract the first 1500 observations.

load Data_EquityIdx
nasdaq = DataTable.NASDAQ(1:1500);

Fit an ARIMA(1,1,1) model to the data.

nasdaqModel = arima(1,1,1);
nasdaqFit = estimate(nasdaqModel,nasdaq);

 
    ARIMA(1,1,1) Model (Gaussian Distribution):
 
                  Value      StandardError    TStatistic      PValue  
                _________    _____________    __________    __________

    Constant      0.43031       0.18555           2.319       0.020393
    AR{1}       -0.074392      0.081985        -0.90739         0.3642
    MA{1}         0.31126      0.077266          4.0284     5.6154e-05
    Variance       27.826       0.63625          43.735              0

Forecast the Composite Index for 500 days using the fitted model. Use the observed data as presample data.

[Y,YMSE] = forecast(nasdaqFit,500,nasdaq);

Plot the forecasts and 95% forecast intervals.

lower = Y - 1.96*sqrt(YMSE);
upper = Y + 1.96*sqrt(YMSE);

figure
plot(nasdaq,'Color',[.7,.7,.7]);
hold on
h1 = plot(1501:2000,lower,'r:','LineWidth',2);
plot(1501:2000,upper,'r:','LineWidth',2)
h2 = plot(1501:2000,Y,'k','LineWidth',2);
legend([h1 h2],'95% Interval','Forecast',...
	     'Location','NorthWest')
title('NASDAQ Composite Index Forecast')
hold off

The process is nonstationary, so the width of each forecast interval grows with time.

Forecast ARX Model

Forecast the following known autoregressive model with one lag and an exogenous predictor (ARX(1)) model into a 10-period forecast horizon:

$$y_t=1+0.3y_{t-1}+2x_t+{\epsilon }_t,$$

where ${\epsilon }_{\mathit{t}}$ is a standard Gaussian random variable, and ${\mathit{x}}_{\mathit{t}}$ is an exogenous Gaussian random variable with a mean of 1 and a standard deviation of 0.5.

Create an arima model object that represents the ARX(1) model.

Mdl = arima('Constant',1,'AR',0.3,'Beta',2,'Variance',1);

To forecast responses from the ARX(1) model, the forecast function requires:

• One presample response ${\mathit{y}}_0$ to initialize the autoregressive term

• Future exogenous data to include the effects of the exogenous variable on the forecasted responses

Set the presample response to the unconditional mean of the stationary process:

$$E(y_t)=\frac{1+2(1)}{1-0.3}.$$

For the future exogenous data, draw 10 values from the distribution of the exogenous variable.

rng(1);
y0 = (1 + 2)/(1 - 0.3);
xf = 1 + 0.5*randn(10,1);

Forecast the ARX(1) model into a 10-period forecast horizon. Specify the presample response and future exogenous data.

fh = 10;
yf = forecast(Mdl,fh,y0,'XF',xf)

yf = 10×1

    3.6367
    5.2722
    3.8232
    3.0373
    3.0657
    3.3470
    3.4454
    4.2120
    4.0667
    4.8065

yf(3) = 3.8232 is the 3-period-ahead forecast of the ARX(1) model.

Forecast Multiple Response Paths

Forecast multiple response paths from a known SAR$\left(1,0,0\right){\left(1,1,0\right)}_4$ model by specifying multiple presample response paths.

Create an arima model object that represents this quarterly SAR$\left(1,0,0\right){\left(1,1,0\right)}_4$ model:

$$(1-0.5L)(1-0.2L^4)(1-L^4)y_t=1+{\epsilon }_t,$$

where ${\epsilon }_{\mathit{t}}$ is a standard Gaussian random variable.

Mdl = arima('Constant',1,'AR',0.5,'Variance',1,...
    'Seasonality',4,'SARLags',4,'SAR',0.2)

Mdl = 
  arima with properties:

     Description: "ARIMA(1,0,0) Model Seasonally Integrated with Seasonal AR(4) (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
               P: 9
               D: 0
               Q: 0
        Constant: 1
              AR: {0.5} at lag [1]
             SAR: {0.2} at lag [4]
              MA: {}
             SMA: {}
     Seasonality: 4
            Beta: [1×0]
        Variance: 1

Because Mdl contains autoregressive dynamic terms, forecast requires the previous Mdl.P responses to generate a $\mathit{t}$-period-ahead forecast from the model. Therefore, the presample must contain at least nine values.

Generate a random 9-by-10 matrix representing 10 presample paths of length 9.

rng(1);
numpaths = 10;
Y0 = rand(Mdl.P,numpaths);

Forecast 10 paths from the SAR model into a 12-quarter forecast horizon. Specify the presample observation paths Y0.

fh = 12;
YF = forecast(Mdl,fh,Y0);

YF is a 12-by-10 matrix of independent forecasted paths. YF(j,k) is the j-period-ahead forecast of path k. Path YF(:,k) represents the continuation of the presample path Y0(:,k).

Plot the presample and forecasts.

Y = [Y0;...
     YF];

figure;
plot(Y);
hold on
h = gca;
px = [6.5 h.XLim([2 2]) 6.5];
py = h.YLim([1 1 2 2]);
hp = patch(px,py,[0.9 0.9 0.9]);
uistack(hp,"bottom");
axis tight
legend("Forecast period")
xlabel('Time (quarters)')
ylabel('Response paths')

Forecast Composite Conditional Mean and Variance Model

Consider the following AR(1) conditional mean model with a GARCH(1,1) conditional variance model for the daily NASDAQ rate series (as a percent) from January 2, 1990 through December 31, 2001.

$$\begin{array}{l}{y}_t=0.073+0.138y_{t-1}+{\epsilon }_t\\ {\sigma }_t^2=0.022+0.873{\sigma }_{t-1}^2+0.119{\epsilon }_{t-1},\end{array}$$

where ${\epsilon }_{\mathit{t}}$ is a series of independent random Gaussian variables with a mean of 0.

Create the model.

CondVarMdl = garch('Constant',0.022,'GARCH',0.873,'ARCH',0.119);
Mdl = arima('Constant',0.073,'AR',0.138,'Variance',CondVarMdl);

Load the equity index data set. Convert the table to a timetable, and convert the NASDAQ price series to a return series. Because the return series has one less observation than the price series, prepad the return series to synchronize it with variables in the timetable.

load Data_EquityIdx
dates = datetime(dates,'ConvertFrom','datenum','Locale','en_US');
TT = table2timetable(DataTable,'RowTimes',dates);
T = size(TT,1);
y0 = 100*price2ret(DataTable.NASDAQ); 
[e0,v0] = infer(Mdl,y0);
n = numel(y0);
TT{:,["NASDAQRet" "Residuals" "CondVar"]} = [nan(T-n,3); y0 e0 v0];

Forecast the model over a 25-day horizon. Supply the entire data set as a presample (forecast uses only the latest required observations to initialize the conditional mean and variance models). Return forecasted responses and conditional variances.

fh = 25;
fhdates = TT.Time(end) + caldays(0:fh);  % Forecast horizon dates
[y,~,v] = forecast(Mdl,fh,TT.NASDAQRet);

Plot the forecasted responses and conditional variances with the observed series from August 2001.

pdates = TT.Time > datetime(2001,8,1);
plot(TT.Time(pdates),TT.NASDAQRet(pdates))
hold on
plot(fhdates,[TT.NASDAQRet(end); y])
hold off

plot(TT.Time(pdates),TT.CondVar(pdates))
hold on
plot(fhdates,[TT.CondVar(end); v]);
hold off

Input Arguments

Mdl — Fully specified ARIMA model

arima model object

Fully specified ARIMA model, specified as an arima model object created by arima or estimate.

The properties of Mdl cannot contain NaN values.

numperiods — Forecast horizon

positive integer

Forecast horizon, or the number of time points in the forecast period, specified as a positive integer.

Data Types: double

Y0 — Presample response data

numeric column vector | numeric matrix

Presample response data paths used to initialize the model for forecasting, specified as a numeric column vector with length numpreobs or a numpreobs-by-numpaths numeric matrix.

Rows of Y0 correspond to periods in the presample, and the last row contains the latest presample response. numpreobs is the number of specified presample responses, which must be at least Mdl.P. If numpreobs exceeds Mdl.P, the forecast function uses only the latest Mdl.P rows. For more details, see Time Base Partitions for Forecasting.

Columns of Y0 correspond to separate, independent presample paths.

• If Y0 is a column vector, forecast applies it to each forecasted path. In this case, all forecast paths Y derive from the same initial conditions.

• If Y0 is a matrix, it must have numpaths columns, where numpaths is the maximum among the second dimensions of the specified presample observation arrays Y0, E0, and V0.

Data Types: double

Name-Value Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: 'X0',X0,'XF',XF specifies the presample and forecasted predictor data X0 and XF, respectively.

E0 — Presample innovations

numeric column vector | numeric matrix

Presample innovations used to initialize either the moving average (MA) component of the ARIMA model or the conditional variance model, specified as a numeric column vector or a numeric matrix with numpaths columns. forecast assumes that the presample innovations have a mean of 0.

Rows of E0 correspond to periods in the presample, and the last row contains the latest presample innovation. E0 must have at least Mdl.Q rows to initialize the MA component. If Mdl.Variance is a conditional variance model (for example, a garch model object), E0 might require more than Mdl.Q rows. If the number of rows exceeds the minimum number required to forecast Mdl, the forecast function uses only the latest required rows.

Columns of E0 correspond to separate, independent presample paths.

• If E0 is a column vector, forecast applies it to each forecasted path. In this case, the MA component and conditional variance model of all forecast paths Y derive from the same initial innovations.

• If E0 is a matrix, it must have numpaths columns.

• By default, if numpreobs ≥ Mdl.P + Mdl.Q, forecast infers any necessary presample innovations by passing the model Mdl and presample data to the infer function. For details on the default for models containing a regression component, see X0 and XF.

• By default, if numpreobs < Mdl.P + Mdl.Q, forecast sets all necessary presample innovations to 0.

Data Types: double

V0 — Presample conditional variances

positive numeric column vector | positive numeric matrix

Presample conditional variances used to initialize the conditional variance model, specified as a positive numeric column vector or a positive numeric matrix with numpaths columns. If the model variance Mdl.Variance is constant, forecast ignores V0.

Rows of V0 correspond to periods in the presample, and the last row contains the latest presample conditional variance. If Mdl.Variance is a conditional variance model (for example, a garch model object), E0 might require more than Mdl.Q rows to initialize Mdl for forecasting. If the number of rows exceeds the minimum number required to forecast Mdl, the forecast function uses only the latest required presample conditional variances.

Columns of V0 correspond to separate, independent presample paths.

• If V0 is a column vector, forecast applies it to each forecasted path. In this case, the conditional variance model of all forecast paths Y derive from the same initial conditional variances.

• If V0 is a matrix, it must have numpaths columns.

By default:

• If you specify enough presample innovations E0 to initialize the conditional variance model Mdl.Variance, forecast infers any necessary presample conditional variances by passing the conditional variance model and E0 to the infer function.

• If you do not specify E0, but you specify enough presample responses Y0 to infer enough presample innovations, then forecast infers any necessary presample conditional variances from the inferred presample innovations.

• If you do not specify enough presample data, forecast sets all necessary presample conditional variances to the unconditional variance of the variance process.

Data Types: double

X0 — Presample predictor data

numeric matrix

Presample predictor data used to infer the presample innovations E0, specified as a numeric matrix with numpreds columns.

Rows of X0 correspond to periods in the presample, and the last row contains the latest set of presample predictor observations. Columns of X0 represent separate time series variables, and they correspond to the columns of XF.

If you do not specify E0, X0 must have at least numpreobs – Mdl.P rows so that forecast can infer presample innovations. If the number of rows exceeds the minimum number required to infer presample innovations, forecast uses only the latest required presample predictor observations. A best practice is to set X0 to the same predictor data matrix used in the estimation, simulation, or inference of Mdl. This setting ensures the correct estimation of the presample innovations E0.

If you specify E0, then forecast ignores X0.

If you specify X0 but you do not specify forecasted predictor data XF, then forecast issues an error.

By default, forecast drops the regression component from the model when it infers presample innovations, regardless of the value of the regression coefficient Mdl.Beta.

Data Types: double

XF — Forecasted (or future) predictor data

numeric matrix

Forecasted (or future) predictor data, specified as a numeric matrix with numpreds columns. XF represents the evolution of specified presample predictor data X0 forecasted into the future (the forecast period).

Rows of XF correspond to time points in the future; XF(t,:) contains the t-period-ahead predictor forecasts. XF must have at least numperiods rows. If the number of rows exceeds numperiods, forecast uses only the first numperiods forecasts. For more details, see Time Base Partitions for Forecasting.

Columns of XF are separate time series variables, and they correspond to the columns of X0.

By default, the forecast function generates forecasts from Mdl without a regression component, regardless of the value of the regression coefficient Mdl.Beta.

Note

forecast assumes that you synchronize all specified presample data sets so that the latest observation of each presample series occurs simultaneously. Similarly, forecast assumes that the first observation in the forecasted predictor data XF occurs in the time point immediately after the last observation in the presample predictor data X0.

Output Arguments

Y — Minimum mean square error forecasts of response series

numeric column vector | numeric matrix

Minimum mean square error (MMSE) forecasts of the conditional mean of the response series, returned as a length numperiods column vector or a numperiods-by-numpaths numeric matrix. Y represents a continuation of Y0 (Y(1,:) occurs in the time point immediately after Y0(end,:)).

Y(t,:) contains the t-period-ahead forecasts, or the conditional mean forecast of all paths for time point t in the forecast period.

forecast determines numpaths from the number of columns in the presample data sets Y0, E0, and V0. For details, see Algorithms. If each presample data set has one column, then Y is a column vector.

Data Types: double

YMSE — MSE of forecasted responses

numeric column vector | numeric matrix

MSE of the forecasted responses Y (forecast error variances), returned as a length numperiods column vector or a numperiods-by-numpaths numeric matrix.

YMSE(t,:) contains the forecast error variances of all paths for time point t in the forecast period.

forecast determines numpaths from the number of columns in the presample data sets Y0, E0, and V0. For details, see Algorithms. If you do not specify any presample data sets, or if each data set is a column vector, then YMSE is a column vector.

The square roots of YMSE are the standard errors of the forecasts Y.

Data Types: double

V — MMSE forecasts of conditional variances of future model innovations

numeric column vector | numeric matrix

MMSE forecasts of the conditional variances of future model innovations, returned as a length numperiods numeric column vector or a numperiods-by-numpaths numeric matrix. V has numperiods rows and numpaths columns.

forecast sets the number of columns of V (numPaths) to the largest number of columns in the presample arrays Y0, E0, and V0. If you do not specify Y0, E0, and V0, then V is a numPeriods column vector.

In all cases, row j contains the conditional variance forecasts of period j.

Data Types: double

More About

Time Base Partitions for Forecasting

Time base partitions for forecasting are two disjoint, contiguous intervals of the time base; each interval contains time series data for forecasting a dynamic model. The forecast period (forecast horizon) is a numperiods length partition at the end of the time base during which the forecast function generates the forecasts Y from the dynamic model Mdl. The presample period is the entire partition occurring before the forecast period. The forecast function can require observed responses Y0, innovations E0, or conditional variances V0 in the presample period to initialize the dynamic model for forecasting. The model structure determines the types and amounts of required presample observations.

A common practice is to fit a dynamic model to a portion of the data set, and then validate the predictability of the model by comparing its forecasts to observed responses. During forecasting, the presample period contains the data to which the model is fit, and the forecast period contains the holdout sample for validation. Suppose that y_t is an observed response series; x_1,t, x_2,t, and x_3,t are observed exogenous series; and time t = 1,…,T. Consider forecasting responses from a dynamic model of y_t containing a regression component with numperiods = K periods. Suppose that the dynamic model is fit to the data in the interval [1,T – K] (for more details, see estimate). This figure shows the time base partitions for forecasting.

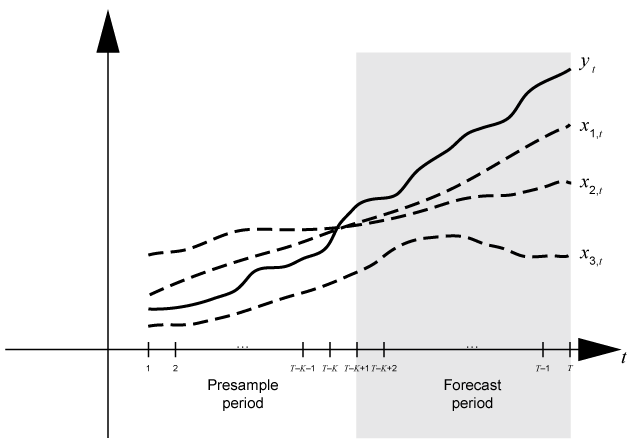
For example, to generate the forecasts Y from an ARX(2) model, forecast requires:

• Presample responses Y0 = $${\left[\begin{array}{cc}{y}_{T-K-1}& y_{T-K}\end{array}\right]}^{\prime }$$ to initialize the model. The 1-period-ahead forecast requires both observations, whereas the 2-periods-ahead forecast requires y_{T – K} and the 1-period-ahead forecast Y(1). The forecast function generates all other forecasts by substituting previous forecasts for lagged responses in the model.

• Future exogenous data XF = $$\left[\begin{array}{ccc}{x}_{1,\left(T-K+1\right):T}& x_{2,\left(T-K+1\right):T}& x_{3,\left(T-K+1\right):T}\end{array}\right]$$ for the model regression component. Without specified future exogenous data, the forecast function ignores the model regression component, which can yield unrealistic forecasts.

Dynamic models containing either a moving average component or a conditional variance model can require presample innovations or conditional variances. Given enough presample responses, forecast infers the required presample innovations and conditional variances. If such a model also contains a regression component, then forecast must have enough presample responses and exogenous data to infer the required presample innovations and conditional variances. This figure shows the arrays of required observations for this case, with corresponding input and output arguments.

Algorithms

• The forecast function sets the number of sample paths (numpaths) to the maximum number of columns among the presample data sets E0, V0, and Y0. All presample data sets must have either one column or numpaths > 1 columns. Otherwise, forecast issues an error. For example, if you supply Y0 and E0, and Y0 has five columns representing five paths, then E0 can each have one column or five columns. If E0 has one column, forecast applies E0 to each path.

• NaN values in presample and future data sets indicate missing data. forecast removes missing data from the presample data sets following this procedure:

  1. forecast horizontally concatenates the specified presample data sets Y0, E0, V0, and X0 so that the latest observations occur simultaneously. The result can be a jagged array because the presample data sets can have a different number of rows. In this case, forecast prepads variables with an appropriate number of zeros to form a matrix.

  2. forecast applies list-wise deletion to the combined presample matrix by removing all rows containing at least one NaN.

  3. forecast extracts the processed presample data sets from the result of step 2, and removes all prepadded zeros.

  forecast applies a similar procedure to the forecasted predictor data XF. After forecast applies list-wise deletion to XF, the result must have at least numperiods rows. Otherwise, forecast issues an error.

  List-wise deletion reduces the sample size and can create irregular time series.

• When forecast estimates the MSEs YMSE of the conditional mean forecasts Y, the function treats the specified predictor data sets X0 and XF as exogenous, nonstochastic, and statistically independent of the model innovations. Therefore, YMSE reflects only the variance associated with the ARIMA component of the input model Mdl.

Compatibility Considerations

Univariate time series models require specification of presample response data to forecast responses

The forecast function now has a third input argument for you to supply presample response data.

forecast(Mdl,numperiods,Y0)
forecast(Mdl,numperiods,Y0,Name,Value)

Before R2019a, the syntaxes were:

forecast(Mdl,numperiods)
forecast(Mdl,numperiods,Name,Value)

You could optionally supply presample responses using the 'Y0' name-value argument.

There are no plans to remove the previous syntaxes or the 'Y0' name-value argument at this time. However, you are encouraged to supply presample responses because, to forecast responses from a dynamic model, forecast must initialize models containing lagged responses. Without specified presample responses, forecast initializes models by using reasonable default values, but these values might not support all workflows.

• For stationary models without a regression component, all presample responses are the unconditional mean of the process, by default.

• For nonstationary models or models containing a regression component, all presample responses are 0, by default.

Update Code

Update your code by specifying presample responses in the third input argument.

If you do not supply presample responses, then forecast provides default presample values that might not support all workflows.

References

[1] Baillie, Richard T., and Tim Bollerslev. “Prediction in Dynamic Models with Time-Dependent Conditional Variances.” Journal of Econometrics 52, (April 1992): 91–113. https://doi.org/10.1016/0304-4076(92)90066-Z.

[2] Bollerslev, Tim. “Generalized Autoregressive Conditional Heteroskedasticity.” Journal of Econometrics 31 (April 1986): 307–27. https://doi.org/10.1016/0304-4076(86)90063-1.

[3] Bollerslev, Tim. “A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return.” The Review of Economics and Statistics 69 (August 1987): 542–47. https://doi.org/10.2307/1925546.

[4] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.

[5] Enders, Walter. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, Inc., 1995.

[6] Engle, Robert. F. “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica 50 (July 1982): 987–1007. https://doi.org/10.2307/1912773.

[7] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.