This example show how to reduce controller order while preserving stability and robustness. This example requires Robust Control Toolbox™ software.
When you use normalized coprime factorization (NCF) balanced truncation with getrom to reduce a plant G or controller K for which the closed-loop response feedback(G*K,eye(n)) is stable, the resulting closed-loop response is also stable as long as the approximation error of the reduced model does not exceed the robustness margin computed by ncfmargin. To see this benefit of NCF balanced truncation, load a plant G and design a controller for it. For this example, use ncfsyn (Robust Control Toolbox) to design the controller.
State-space model with 1 outputs, 1 inputs, and 3 states.
State-space model with 1 outputs, 1 inputs, and 5 states.
ncfsyn designs a controller by optimizing the ncfmargin robustness margin using a plant shaped by weighting functions W1 and W2 (see ncfsyn (Robust Control Toolbox)). To analyze margins with ncfmargin and reduce controller order, work with the shaped plant Gs and the controller Ks designed for it.
Use ncfmargin (Robust Control Toolbox) to find the robustness margin of the system with the full-order controller. ncfsyn assumes a positive feedback loop while ncfmargin assumes negative feedback, so reverse the sign of the controller for this computation.
As long as the approximation error of the reduced-order controller does not exceed emax, stability of the closed-loop system is preserved.
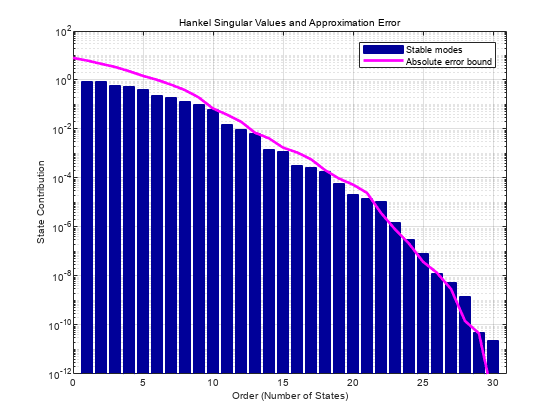
Create a model order reduction task using reducespec.
To select the reduced order, visualize the errors associated with each target order.
Suppose that you can tolerate up to a 50% reduction in this margin in exchange for the computational benefit of a lower order controller.
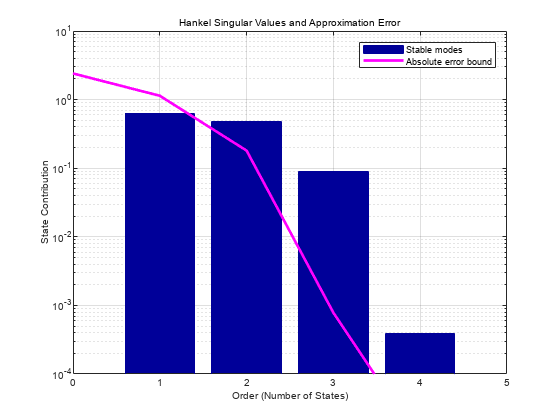
Obtain the reduced-order model such that the target error does not exceed emax/2.
State-space model with 1 outputs, 1 inputs, and 3 states.
The reduced-order controller yields a very similar stability margin to the original controller.
Reducing the controller order further leads to additional reduction in the stability margin. Reducing too far can lead to loss of closed-loop stability. For instance, try reducing to first order.
Thus, for further analysis or implementation, use the third-order controller. To do so, convert Ksr, the reduced controller for Gs, into Kr, the reduced controller for G.
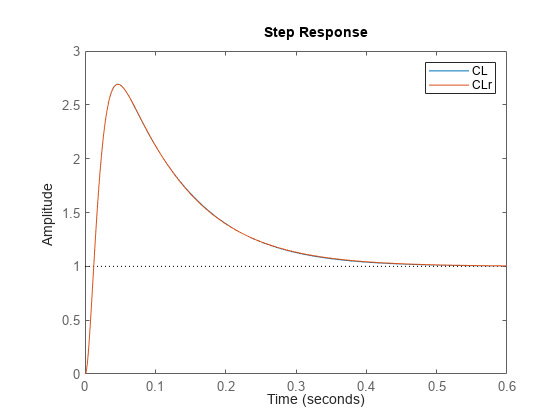
To confirm that this controller is satisfactory, compare the closed-loop response to the response with the full-order controller. Again, reverse the sign of the controller to account for ncfsyn assuming positive feedback.
The large overshoot in this case is due to instability of the original plant G.