Main Content

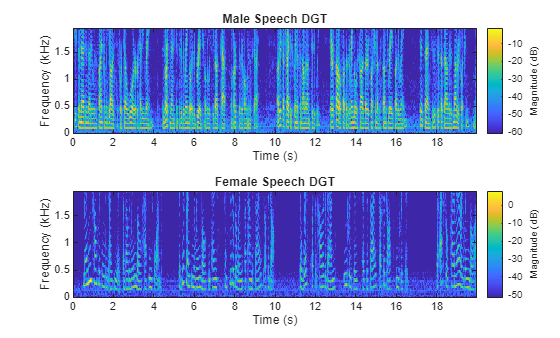
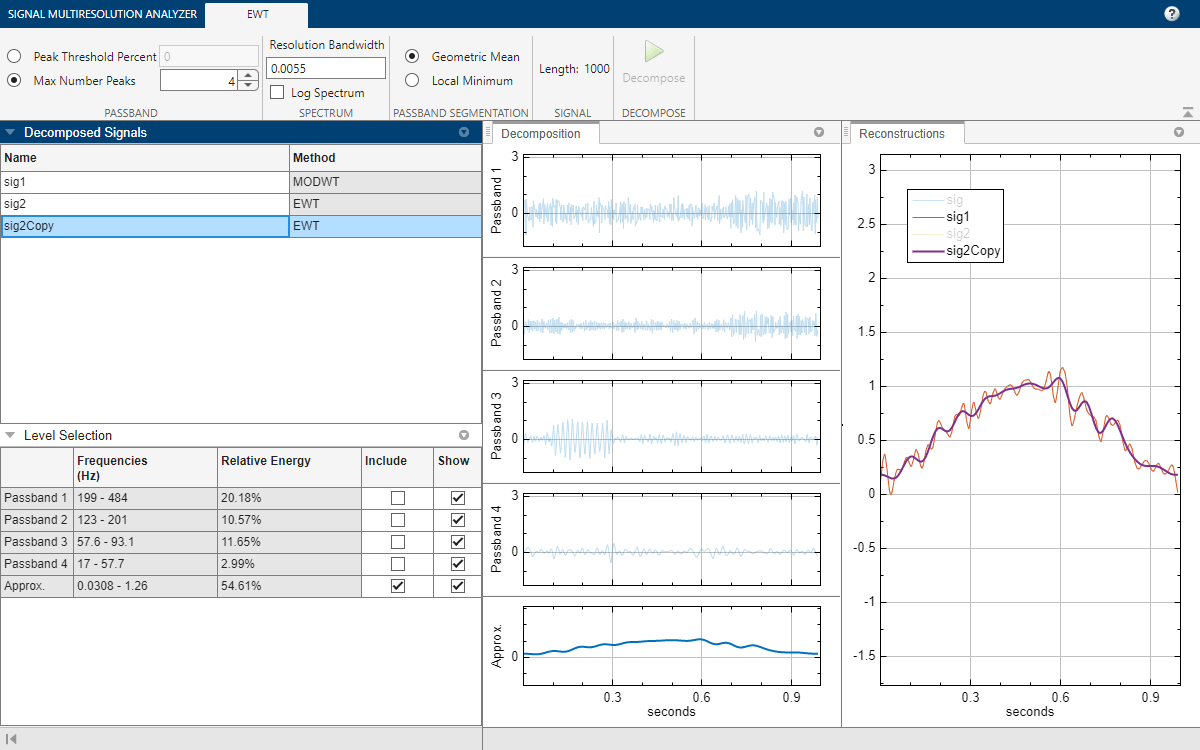
상수-Q 변환, 데이터 적응적 변환 및 2차 시간-주파수 변환

1차원 CQT, 1차원 역 CQT, 경험적 웨이블릿 변환, 경험적 모드 분해, 힐베르트-황 변환, 위그너-빌 분포

신호의 CQT(상수-Q 변환)를 구하고 완벽한 복원을 위해 변환을 역변환합니다. 적응형 웨이블릿 세분화 방식을 사용하여 신호를 분해합니다. 비선형 및 비정상 과정에 대해 데이터 적응적 시간-주파수 분석을 수행합니다. 비선형 또는 비정상 과정을 진동의 내재 모드로 분해합니다. 다중 성분 비선형 신호 또는 비정상 신호의 순시 주파수 추정값을 구합니다. 신호의 위그너-빌 분포 및 상호 위그너-빌 분포를 반환합니다.

함수

cqtConstant-Q nonstationary Gabor transform
icqtInverse constant-Q transform using nonstationary Gabor frames
emd경험적 모드 분해
ewtEmpirical wavelet transform (R2020b 이후)
hht힐베르트-황 변환(Hilbert-Huang Transform)
vmdVariational mode decomposition (R2020a 이후)
wvd위그너-빌 분포 및 평활화된 유사 위그너-빌 분포
xwvdCross Wigner-Ville distribution and cross smoothed pseudo Wigner-Ville distribution

앱

신호 다중분해능 분석기Decompose signals into time-aligned components

도움말 항목