loss

Class: FeatureSelectionNCAClassification

Evaluate accuracy of learned feature weights on test data

Syntax

err = loss(mdl,X,Y)
err = loss(mdl,X,Y,Name,Value)


Description

err = loss(mdl,X,Y) computes the misclassification error of the model mdl, for the predictors in X and the class labels in Y.

err = loss(mdl,X,Y,Name,Value) computes the classification error with additional options specified by one or more Name,Value pair arguments.

Input Arguments

mdl — Neighborhood component analysis model for classification

FeatureSelectionNCAClassification object

Neighborhood component analysis model for classification, returned as a FeatureSelectionNCAClassification object.

X — Predictor variable values

n-by-p matrix

Predictor variable values, specified as an n-by-p matrix, where n is the number of observations and p is the number of predictor variables.

Data Types: single | double

Y — Class labels

categorical vector | logical vector | numeric vector | string array | cell array of character vectors of length n | character matrix with n rows

Class labels, specified as a categorical vector, logical vector, numeric vector, string array, cell array of character vectors of length n, or character matrix with n rows, where n is the number of observations. Element i or row i of Y is the class label corresponding to row i of X (observation i).

Data Types: single | double | logical | char | string | cell | categorical

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

'LossFunction' — Loss function type

'classiferror' (default) | 'quadratic'

Loss function type, specified as a comma-separated pair consisting of 'Loss Function' and one of the following.

• 'classiferror' — Misclassification error, defined as

  $$\frac{1}{n}{\displaystyle \sum _{i=1}^{n}I\left(k_i\ne t_i\right)},$$

  where $$k_i$$ is the predicted class and $$t_i$$ is the true class for observation i. $$I\left(k_i\ne t_i\right)$$ is the indicator for when the $$k_i$$ is not the same as $$t_i$$.

• 'quadratic' — Quadratic loss function, defined as

  $$\frac{1}{n}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^c{\left(p_{ik}-I\left(i,k\right)\right)}^2,}}$$

  where c is the number of classes, $$p_{ik}$$ is the estimate probability that ith observation belongs to class k, and $$I\left(i,k\right)$$ is the indicator that ith observation belongs to class k.

Example: 'LossFunction','quadratic'

Output Arguments

err — Smaller-the-better accuracy measure for learned feature weights

scalar value

Smaller-the-better accuracy measure for learned feature weights, returned as a scalar value. You can specify the measure of accuracy using the LossFunction name-value pair argument.

Examples

Tune NCA Model for Classification

Load the sample data.

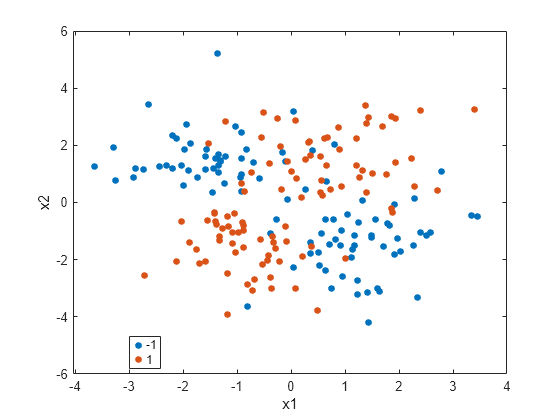
load('twodimclassdata.mat');

This data set is simulated using the scheme described in [1]. This is a two-class classification problem in two dimensions. Data from the first class (class –1) are drawn from two bivariate normal distributions or with equal probability, where , , and . Similarly, data from the second class (class 1) are drawn from two bivariate normal distributions or with equal probability, where , , and . The normal distribution parameters used to create this data set result in tighter clusters in data than the data used in [1].

Create a scatter plot of the data grouped by the class.

figure
gscatter(X(:,1),X(:,2),y)
xlabel('x1')
ylabel('x2')

Add 100 irrelevant features to . First generate data from a Normal distribution with a mean of 0 and a variance of 20.

n = size(X,1);
rng('default')
XwithBadFeatures = [X,randn(n,100)*sqrt(20)];

Normalize the data so that all points are between 0 and 1.

XwithBadFeatures = bsxfun(@rdivide,...
    bsxfun(@minus,XwithBadFeatures,min(XwithBadFeatures,[],1)), ...
    range(XwithBadFeatures,1));
X = XwithBadFeatures;

Fit a neighborhood component analysis (NCA) model to the data using the default Lambda (regularization parameter, ) value. Use the LBFGS solver and display the convergence information.

ncaMdl = fscnca(X,y,'FitMethod','exact','Verbose',1, ...
              'Solver','lbfgs');

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  9.519258e-03 |   1.494e-02 |   0.000e+00 |        |   4.015e+01 |   0.000e+00 |   YES  |
|        1 | -3.093574e-01 |   7.186e-03 |   4.018e+00 |    OK  |   8.956e+01 |   1.000e+00 |   YES  |
|        2 | -4.809455e-01 |   4.444e-03 |   7.123e+00 |    OK  |   9.943e+01 |   1.000e+00 |   YES  |
|        3 | -4.938877e-01 |   3.544e-03 |   1.464e+00 |    OK  |   9.366e+01 |   1.000e+00 |   YES  |
|        4 | -4.964759e-01 |   2.901e-03 |   6.084e-01 |    OK  |   1.554e+02 |   1.000e+00 |   YES  |
|        5 | -4.972077e-01 |   1.323e-03 |   6.129e-01 |    OK  |   1.195e+02 |   5.000e-01 |   YES  |
|        6 | -4.974743e-01 |   1.569e-04 |   2.155e-01 |    OK  |   1.003e+02 |   1.000e+00 |   YES  |
|        7 | -4.974868e-01 |   3.844e-05 |   4.161e-02 |    OK  |   9.835e+01 |   1.000e+00 |   YES  |
|        8 | -4.974874e-01 |   1.417e-05 |   1.073e-02 |    OK  |   1.043e+02 |   1.000e+00 |   YES  |
|        9 | -4.974874e-01 |   4.893e-06 |   1.781e-03 |    OK  |   1.530e+02 |   1.000e+00 |   YES  |
|       10 | -4.974874e-01 |   9.404e-08 |   8.947e-04 |    OK  |   1.670e+02 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 9.404e-08
              Two norm of the final step     = 8.947e-04, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 9.404e-08, TolFun = 1.000e-06
EXIT: Local minimum found.

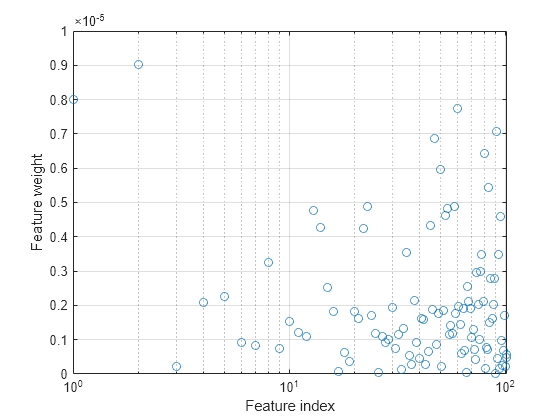
Plot the feature weights. The weights of the irrelevant features should be very close to zero.

figure
semilogx(ncaMdl.FeatureWeights,'ro')
xlabel('Feature index')
ylabel('Feature weight')
grid on

Predict the classes using the NCA model and compute the confusion matrix.

ypred = predict(ncaMdl,X);
confusionchart(y,ypred)

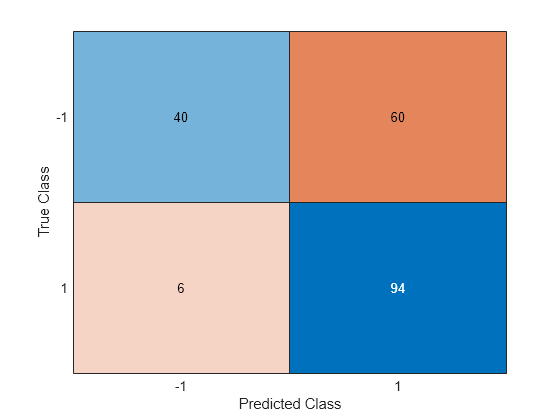
Confusion matrix shows that 40 of the data that are in class –1 are predicted as belonging to class –1. 60 of the data from class –1 are predicted to be in class 1. Similarly, 94 of the data from class 1 are predicted to be from class 1 and 6 of them are predicted to be from class –1. The prediction accuracy for class –1 is not good.

All weights are very close to zero, which indicates that the value of used in training the model is too large. When , all features weights approach to zero. Hence, it is important to tune the regularization parameter in most cases to detect the relevant features.

Use five-fold cross-validation to tune for feature selection by using fscnca. Tuning means finding the value that will produce the minimum classification loss. To tune using cross-validation:

1. Partition the data into five folds. For each fold, cvpartition assigns four-fifths of the data as a training set and one-fifth of the data as a test set. Again for each fold, cvpartition creates a stratified partition, where each partition has roughly the same proportion of classes.

cvp = cvpartition(y,'kfold',5);
numtestsets = cvp.NumTestSets;
lambdavalues = linspace(0,2,20)/length(y);
lossvalues = zeros(length(lambdavalues),numtestsets);

2. Train the neighborhood component analysis (nca) model for each value using the training set in each fold.

3. Compute the classification loss for the corresponding test set in the fold using the nca model. Record the loss value.

4. Repeat this process for all folds and all values.

for i = 1:length(lambdavalues)
    for k = 1:numtestsets

        % Extract the training set from the partition object
        Xtrain = X(cvp.training(k),:);
        ytrain = y(cvp.training(k),:);

        % Extract the test set from the partition object
        Xtest  = X(cvp.test(k),:);
        ytest  = y(cvp.test(k),:);

        % Train an NCA model for classification using the training set
        ncaMdl = fscnca(Xtrain,ytrain,'FitMethod','exact', ...
            'Solver','lbfgs','Lambda',lambdavalues(i));

        % Compute the classification loss for the test set using the NCA
        % model
        lossvalues(i,k) = loss(ncaMdl,Xtest,ytest, ...
            'LossFunction','quadratic');

    end
end

Plot the average loss values of the folds versus the values. If the value that corresponds to the minimum loss falls on the boundary of the tested values, the range of values should be reconsidered.

figure
plot(lambdavalues,mean(lossvalues,2),'ro-')
xlabel('Lambda values')
ylabel('Loss values')
grid on

Find the value that corresponds to the minimum average loss.

[~,idx] = min(mean(lossvalues,2)); % Find the index
bestlambda = lambdavalues(idx) % Find the best lambda value

bestlambda =

    0.0037

Fit the NCA model to all of the data using the best value. Use the LBFGS solver and display the convergence information.

ncaMdl = fscnca(X,y,'FitMethod','exact','Verbose',1, ...
        'Solver','lbfgs','Lambda',bestlambda);

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 | -1.246913e-01 |   1.231e-02 |   0.000e+00 |        |   4.873e+01 |   0.000e+00 |   YES  |
|        1 | -3.411330e-01 |   5.717e-03 |   3.618e+00 |    OK  |   1.068e+02 |   1.000e+00 |   YES  |
|        2 | -5.226111e-01 |   3.763e-02 |   8.252e+00 |    OK  |   7.825e+01 |   1.000e+00 |   YES  |
|        3 | -5.817731e-01 |   8.496e-03 |   2.340e+00 |    OK  |   5.591e+01 |   5.000e-01 |   YES  |
|        4 | -6.132632e-01 |   6.863e-03 |   2.526e+00 |    OK  |   8.228e+01 |   1.000e+00 |   YES  |
|        5 | -6.135264e-01 |   9.373e-03 |   7.341e-01 |    OK  |   3.244e+01 |   1.000e+00 |   YES  |
|        6 | -6.147894e-01 |   1.182e-03 |   2.933e-01 |    OK  |   2.447e+01 |   1.000e+00 |   YES  |
|        7 | -6.148714e-01 |   6.392e-04 |   6.688e-02 |    OK  |   3.195e+01 |   1.000e+00 |   YES  |
|        8 | -6.149524e-01 |   6.521e-04 |   9.934e-02 |    OK  |   1.236e+02 |   1.000e+00 |   YES  |
|        9 | -6.149972e-01 |   1.154e-04 |   1.191e-01 |    OK  |   1.171e+02 |   1.000e+00 |   YES  |
|       10 | -6.149990e-01 |   2.922e-05 |   1.983e-02 |    OK  |   7.365e+01 |   1.000e+00 |   YES  |
|       11 | -6.149993e-01 |   1.556e-05 |   8.354e-03 |    OK  |   1.288e+02 |   1.000e+00 |   YES  |
|       12 | -6.149994e-01 |   1.147e-05 |   7.256e-03 |    OK  |   2.332e+02 |   1.000e+00 |   YES  |
|       13 | -6.149995e-01 |   1.040e-05 |   6.781e-03 |    OK  |   2.287e+02 |   1.000e+00 |   YES  |
|       14 | -6.149996e-01 |   9.015e-06 |   6.265e-03 |    OK  |   9.974e+01 |   1.000e+00 |   YES  |
|       15 | -6.149996e-01 |   7.763e-06 |   5.206e-03 |    OK  |   2.919e+02 |   1.000e+00 |   YES  |
|       16 | -6.149997e-01 |   8.374e-06 |   1.679e-02 |    OK  |   6.878e+02 |   1.000e+00 |   YES  |
|       17 | -6.149997e-01 |   9.387e-06 |   9.542e-03 |    OK  |   1.284e+02 |   5.000e-01 |   YES  |
|       18 | -6.149997e-01 |   3.250e-06 |   5.114e-03 |    OK  |   1.225e+02 |   1.000e+00 |   YES  |
|       19 | -6.149997e-01 |   1.574e-06 |   1.275e-03 |    OK  |   1.808e+02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       20 | -6.149997e-01 |   5.764e-07 |   6.765e-04 |    OK  |   2.905e+02 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 5.764e-07
              Two norm of the final step     = 6.765e-04, TolX   = 1.000e-06
Relative infinity norm of the final gradient = 5.764e-07, TolFun = 1.000e-06
EXIT: Local minimum found.

Plot the feature weights.

figure
semilogx(ncaMdl.FeatureWeights,'ro')
xlabel('Feature index')
ylabel('Feature weight')
grid on

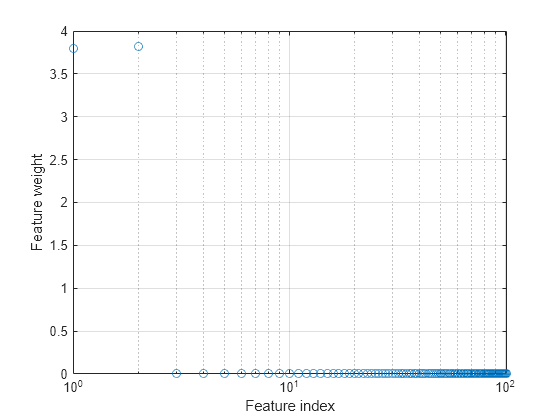
fscnca correctly figures out that the first two features are relevant and that the rest are not. The first two features are not individually informative, but when taken together result in an accurate classification model.

Predict the classes using the new model and compute the accuracy.

ypred = predict(ncaMdl,X);
confusionchart(y,ypred)

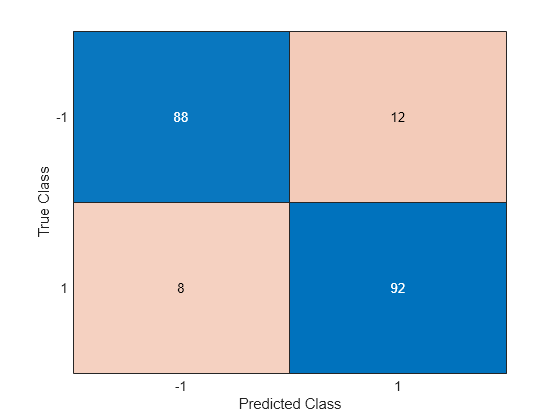
Confusion matrix shows that prediction accuracy for class –1 has improved. 88 of the data from class –1 are predicted to be from –1, and 12 of them are predicted to be from class 1. 92 of the data from class 1 are predicted to be from class 1 and 8 of them are predicted to be from class –1.

References

[1] Yang, W., K. Wang, W. Zuo. "Neighborhood Component Feature Selection for High-Dimensional Data." Journal of Computers. Vol. 7, Number 1, January, 2012.