knnsearch
Find k-nearest neighbors using searcher object
Description
Idx = knnsearch(Mdl,Y)Mdl.X to each point (i.e., row or observation) in the query
data Y using an exhaustive search, a Kd-tree,
or a Hierarchical Navigable Small Worlds approximate search.
knnsearch returns Idx, which is a column
vector of the indices in Mdl.X representing the nearest
neighbors.
Idx = knnsearch(Mdl,Y,Name,Value)Mdl.X to
Y with additional options specified by one or more
Name,Value pair arguments. For example, specify the number of
nearest neighbors to search for, or distance metric different from the one stored in
Mdl.Distance. You can also specify which action to take if
the closest distances are tied.
[ additionally returns the matrix
Idx,D]
= knnsearch(___)D using any of the input arguments in the previous syntaxes.
D contains the distances between each observation in
Y that correspond to the closest observations in
Mdl.X. By default, the function arranges the columns of
D in ascending order by closeness, with respect to the
distance metric.
Examples
knnsearch accepts ExhaustiveSearcher or KDTreeSearcher model objects to search the training data for the nearest neighbors to the query data. An ExhaustiveSearcher model invokes the exhaustive searcher algorithm, and a KDTreeSearcher model defines a Kd-tree, which knnsearch uses to search for nearest neighbors.
Load Fisher's iris data set. Randomly reserve five observations from the data for query data.
load fisheriris rng(1); % For reproducibility n = size(meas,1); idx = randsample(n,5); X = meas(~ismember(1:n,idx),:); % Training data Y = meas(idx,:); % Query data
The variable meas contains 4 predictors.
Grow a default four-dimensional Kd-tree.
MdlKDT = KDTreeSearcher(X)
MdlKDT =
KDTreeSearcher with properties:
BucketSize: 50
Distance: 'euclidean'
DistParameter: []
X: [145×4 double]
MdlKDT is a KDTreeSearcher model object. You can alter its writable properties using dot notation.
Prepare an exhaustive nearest neighbor searcher.
MdlES = ExhaustiveSearcher(X)
MdlES =
ExhaustiveSearcher with properties:
Distance: 'euclidean'
DistParameter: []
X: [145×4 double]
MdlKDT is an ExhaustiveSearcher model object. It contains the options, such as the distance metric, to use to find nearest neighbors.
Alternatively, you can grow a Kd-tree or prepare an exhaustive nearest neighbor searcher using createns.
Search the training data for the nearest neighbors indices that correspond to each query observation. Conduct both types of searches using the default settings. By default, the number of neighbors to search for per query observation is 1.
IdxKDT = knnsearch(MdlKDT,Y); IdxES = knnsearch(MdlES,Y); [IdxKDT IdxES]
ans = 5×2
17 17
6 6
1 1
89 89
124 124
In this case, the results of the search are the same.
Grow a Kd-tree nearest neighbor searcher object by using the createns function. Pass the object and query data to the knnsearch function to find k-nearest neighbors.
Load Fisher's iris data set.
load fisheririsRemove five irises randomly from the predictor data to use as a query set.
rng(1) % For reproducibility n = size(meas,1); % Sample size qIdx = randsample(n,5); % Indices of query data tIdx = ~ismember(1:n,qIdx); % Indices of training data Q = meas(qIdx,:); X = meas(tIdx,:);
Grow a four-dimensional Kd-tree using the training data. Specify the Minkowski distance for finding nearest neighbors.
Mdl = createns(X,'Distance','minkowski')
Mdl =
KDTreeSearcher with properties:
BucketSize: 50
Distance: 'minkowski'
DistParameter: 2
X: [145×4 double]
Because X has four columns and the distance metric is Minkowski, createns creates a KDTreeSearcher model object by default. The Minkowski distance exponent is 2 by default.
Find the indices of the training data (Mdl.X) that are the two nearest neighbors of each point in the query data (Q).
IdxNN = knnsearch(Mdl,Q,'K',2)IdxNN = 5×2
17 4
6 2
1 12
89 66
124 100
Each row of IdxNN corresponds to a query data observation, and the column order corresponds to the order of the nearest neighbors, with respect to ascending distance. For example, based on the Minkowski distance, the second nearest neighbor of Q(3,:) is X(12,:).
Load Fisher's iris data set.
load fisheririsRemove five irises randomly from the predictor data to use as a query set.
rng(4); % For reproducibility n = size(meas,1); % Sample size qIdx = randsample(n,5); % Indices of query data X = meas(~ismember(1:n,qIdx),:); Y = meas(qIdx,:);
Grow a four-dimensional Kd-tree using the training data. Specify the Minkowski distance for finding nearest neighbors.
Mdl = KDTreeSearcher(X);
Mdl is a KDTreeSearcher model object. By default, the distance metric for finding nearest neighbors is the Euclidean metric.
Find the indices of the training data (X) that are the seven nearest neighbors of each point in the query data (Y).
[Idx,D] = knnsearch(Mdl,Y,'K',7,'IncludeTies',true);
Idx and D are five-element cell arrays of vectors, with each vector having at least seven elements.
Display the lengths of the vectors in Idx.
cellfun('length',Idx)ans = 5×1
8
7
7
7
7
Because cell 1 contains a vector with length greater than k = 7, query observation 1 (Y(1,:)) is equally close to at least two observations in X.
Display the indices of the nearest neighbors to Y(1,:) and their distances.
nn5 = Idx{1}nn5 = 1×8
91 98 67 69 71 93 88 95
nn5d = D{1}nn5d = 1×8
0.1414 0.2646 0.2828 0.3000 0.3464 0.3742 0.3873 0.3873
Training observations 88 and 95 are 0.3873 cm away from query observation 1.
Train two KDTreeSearcher models using different distance metrics, and compare k-nearest neighbors of query data for the two models.
Load Fisher's iris data set. Consider the petal measurements as predictors.
load fisheriris X = meas(:,3:4); % Predictors Y = species; % Response
Train a KDTreeSearcher model object by using the predictors. Specify the Minkowski distance with exponent 5.
KDTreeMdl = KDTreeSearcher(X,'Distance','minkowski','P',5)
KDTreeMdl =
KDTreeSearcher with properties:
BucketSize: 50
Distance: 'minkowski'
DistParameter: 5
X: [150×2 double]
Find the 10 nearest neighbors from X to a query point (newpoint), first using Minkowski then Chebychev distance metrics. The query point must have the same column dimension as the data used to train the model.
newpoint = [5 1.45]; [IdxMk,DMk] = knnsearch(KDTreeMdl,newpoint,'k',10); [IdxCb,DCb] = knnsearch(KDTreeMdl,newpoint,'k',10,'Distance','chebychev');
IdxMk and IdxCb are 1-by-10 matrices containing the row indices of X corresponding to the nearest neighbors to newpoint using Minkowski and Chebychev distances, respectively. Element (1,1) is the nearest, element (1,2) is the next nearest, and so on.
Plot the training data, query point, and nearest neighbors.
figure; gscatter(X(:,1),X(:,2),Y); title('Fisher''s Iris Data -- Nearest Neighbors'); xlabel('Petal length (cm)'); ylabel('Petal width (cm)'); hold on plot(newpoint(1),newpoint(2),'kx','MarkerSize',10,'LineWidth',2); % Query point plot(X(IdxMk,1),X(IdxMk,2),'o','Color',[.5 .5 .5],'MarkerSize',10); % Minkowski nearest neighbors plot(X(IdxCb,1),X(IdxCb,2),'p','Color',[.5 .5 .5],'MarkerSize',10); % Chebychev nearest neighbors legend('setosa','versicolor','virginica','query point',... 'minkowski','chebychev','Location','Best');

Zoom in on the points of interest.
h = gca; % Get current axis handle. h.XLim = [4.5 5.5]; h.YLim = [1 2]; axis square;
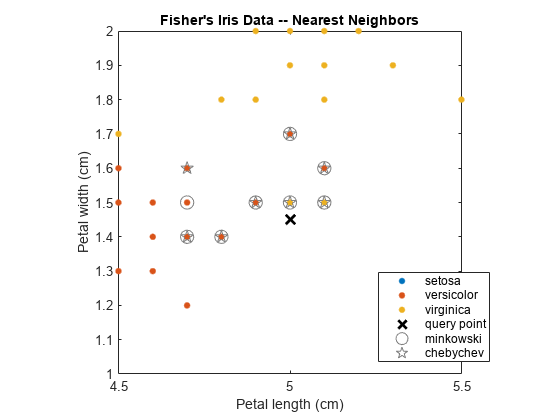
Several observations are equal, which is why only eight nearest neighbors are identified in the plot.
Create a large data set and compare the speed of an HNSW searcher to the speed of an exhaustive searcher for 1000 query points.
Create the data.
rng default % For reproducibility A = diag(1:100); B = randn(100,10); K = kron(A,B); ss = size(K)
ss = 1×2
10000 1000
The data K has 1e4 rows and 1e3 columns.
Create an HNSW searcher object h from the data K.
tic; h = hnswSearcher(K); chnsw = toc
chnsw = 10.6544
Create 1000 random query points with 1000 features (columns). Specify to search for five nearest neighbors.
Y = randn(1000, 1000); tic; [idx, D] = knnsearch(h,Y,K=5); thnsw = toc
thnsw = 0.0797
Create an exhaustive searcher object e from the data K.
tic e = ExhaustiveSearcher(K); ces = toc
ces = 0.0021
Creating an exhaustive searcher is much faster than creating an HNSW searcher.
Time the search using e and compare the result to the time using the HNSW searcher h.
tic; [idx0, D0] = knnsearch(e,Y,K=5); tes = toc
tes = 1.4841
In this case, the HNSW searcher computes about 20 times faster than the exhaustive searcher.
Determine how many results of the HNSW search differ in some way from the results of the exhaustive search.
v = abs(idx - idx0); % Count any difference in the five found entries vv = sum(v,2); % vv = 0 means no difference nz = nnz(vv) % Out of 1000 rows how many differ at all?
nz = 118
Here, 118 of 1000 HNSW search results differ from the exhaustive search results.
Try to improve the accuracy of the HNSW searcher by training with nondefault parameters. Specifically, use larger values for MaxNumLinksPerNode and TrainSetSize. These settings affect the speed of training and finding nearest neighbors.
tic; h2 = hnswSearcher(K,MaxNumLinksPerNode=48,TrainSetSize=2000); chnsw2 = toc
chnsw2 = 78.4836
With these parameters, the searcher takes about seven times as long to train.
tic; [idx2, D2] = knnsearch(h2,Y,K=5); thnsw2 = toc
thnsw2 = 0.1049
The speed of finding nearest neighbors using HNSW decreases, but is still more than ten times faster than the exhaustive search.
v = abs(idx2 - idx0); vv = sum(v,2); nz = nnz(vv)
nz = 57
For the slower but more accurate HNSW search, only 57 of 1000 results differ in any way from the exact results. Summarize the timing results in a table.
timet = table([chnsw;ces;chnsw2],[thnsw;tes;thnsw2],'RowNames',["HNSW";"Exhaustive";"HNSW2"],'VariableNames',["Creation" "Search"])
timet=3×2 table
Creation Search
_________ ________
HNSW 10.654 0.079741
Exhaustive 0.0021304 1.4841
HNSW2 78.484 0.10492
Input Arguments
Nearest neighbor searcher, specified as an ExhaustiveSearcher, KDTreeSearcher, or hnswSearcher
model object.
If Mdl is an ExhaustiveSearcher model, then
knnsearch searches for nearest neighbors using an exhaustive
search. If Mdl is a KDTreeSearcher model,
knnsearch uses the grown Kd-tree to search
for nearest neighbors. If Mdl is an hnswSearcher
model, knnsearch uses the Hierarchical Navigable Small Worlds
approximate neighbor search algorithm. For descriptions, see k-Nearest Neighbor Search and Radius Search.
Query data, specified as a numeric matrix.
Y is an m-by-K matrix.
Rows of Y correspond to observations (i.e., examples),
and columns correspond to predictors (i.e., variables or features). Y must
have the same number of columns as the training data stored in Mdl.X.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'K',2,'Distance','minkowski' specifies to find the two
nearest neighbors of Mdl.X to each point in Y
and to use the Minkowski distance metric.
For Exhaustive Nearest Neighbor Searchers and Kd-Tree Nearest Neighbor Searchers
Distance metric used to find neighbors of the training data to the query observations, specified as one of the values in this table or function handle.
For all types of nearest neighbor searchers, knnsearch supports these
distance metrics.
| Value | Description |
|---|---|
'chebychev' | Chebychev distance (maximum coordinate difference) |
'cityblock' | City block distance |
'euclidean' | Euclidean distance |
'minkowski' | Minkowski distance. The default exponent is 2. To specify a different exponent, use the
'P' name-value
argument. |
If Mdl is an ExhaustiveSearcher model object, then
knnsearch also supports these distance metrics.
| Value | Description |
|---|---|
'correlation' | One minus the sample linear correlation between observations (treated as sequences of values) |
'cosine' | One minus the cosine of the included angle between observations (treated as row vectors) |
'fasteuclidean' | Euclidean distance computed by using an alternative algorithm that saves time
when the number of predictors is at least 10. In some cases, this faster algorithm can
reduce accuracy. This distance metric is available only when
NSMethod is 'exhaustive'. Algorithms
starting with 'fast' do not support sparse data. For details, see
Algorithms. |
'fastseuclidean' | Standardized Euclidean distance computed by using an alternative algorithm that
saves time when the number of predictors is at least 10. In some cases, this faster
algorithm can reduce accuracy. This distance metric is available only when
NSMethod is 'exhaustive'. Algorithms
starting with 'fast' do not support sparse data. For details, see
Algorithms. |
'hamming' | Hamming distance, which is the percentage of coordinates that differ |
'jaccard' | One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ |
'mahalanobis' | Mahalanobis distance, computed using a positive definite covariance matrix. To change the
value of the covariance matrix, use the 'Cov' name-value
argument. |
'seuclidean' | Standardized Euclidean distance. Each coordinate difference between the rows in
X and the query matrix Y is scaled by
dividing by the corresponding element of the standard deviation computed from
X. To specify a different scaling, use the
'Scale' name-value argument. |
'spearman' | One minus the sample Spearman's rank correlation between observations (treated as sequences of values) |
If Mdl is an hnswSearcher model object,
knnsearch supports all the distances in the
ExhaustiveSearcher table except for those beginning with
fast: "fasteuclidean" and
"fastseuclidean".
If Mdl is an ExhaustiveSearcher model object, then you
can also specify a function handle for a custom distance metric
by using @ (for example,
@distfun). The custom distance
function must:
Have the form
function D2 = distfun(ZI,ZJ).Take as arguments:
A 1-by-K vector
ZIcontaining a single row fromMdl.XorY, where K is the number of columns ofMdl.X.An m-by-K matrix
ZJcontaining multiple rows ofMdl.XorY, where m is a positive integer.
Return an m-by-1 vector of distances
D2, whereD2(is the distance between the observationsj)ZIandZJ(.j,:)
For more details, see Distance Metrics.
Example: 'Distance','minkowski'
Data Types: char | string | function_handle
Flag to include nearest neighbors that have the same distance from
query observations, specified as the comma-separated pair consisting of
'IncludeTies' and false
(0) or true
(1).
If IncludeTies is true, then:
knnsearchincludes all nearest neighbors whose distances are equal to the kth smallest distance in the output arguments, where k is the number of searched nearest neighbors specified by the'K'name-value pair argument.IdxandDare m-by-1cell arrays such that each cell contains a vector of at least k indices and distances, respectively. Each vector inDcontains arranged distances in ascending order. Each row inIdxcontains the indices of the nearest neighbors corresponding to the distances inD.
If IncludeTies is
false, then knnsearch chooses
the observation with the smallest index among the observations that have
the same distance from a query point.
Example: 'IncludeTies',true
Number of nearest neighbors to search for in the training data per
query observation, specified as the comma-separated pair consisting of
'K' and a positive integer.
Example: 'K',2
Data Types: single | double
Exponent for the Minkowski distance metric, specified as a positive scalar. This argument is
valid only when Distance is
"minkowski".
The value of P sets the value of the
DistParameter property in the model
object.
Example: P=3
Data Types: single | double
For Kd-Tree Nearest Neighbor Searchers
Flag to sort returned indices according to distance, specified as the
comma-separated pair consisting of 'SortIndices' and
either true (1) or
false (0).
For faster performance, you can set SortIndices
to false when the following are true:
Ycontains many observations that have many nearest neighbors inX.Mdlis aKDTreeSearchermodel object.IncludeTiesisfalse.
In this case, knnsearch returns the
indices of the nearest neighbors in no particular order. When
SortIndices is true, the
function arranges the nearest neighbor indices in ascending order by
distance.
SortIndices is true by
default. When Mdl is an
ExhaustiveSearcher model object or
IncludeTies is true, the
function always sorts the indices.
Example: 'SortIndices',false
Data Types: logical
For Exhaustive Nearest Neighbor Searchers
Covariance matrix for the Mahalanobis distance metric, specified as the comma-separated pair
consisting of 'Cov' and a positive definite matrix.
Cov is a K-by-K matrix,
where K is the number of columns of Mdl.X. If you
specify Cov and do not specify
'Distance','mahalanobis',
then knnsearch returns an error message.
Example: 'Cov',eye(3)
Data Types: single | double
Scale parameter value for the standardized Euclidean distance metric, specified as the
comma-separated pair consisting of 'Scale' and a nonnegative numeric
vector. Scale has length K, where
K is the number of columns of Mdl.X.
The software scales each difference between the training and query data using the
corresponding element of Scale. If you specify
Scale and do not specify
'Distance','seuclidean',
then knnsearch returns an error message.
Example: 'Scale',quantile(Mdl.X,0.75) -
quantile(Mdl.X,0.25)
Data Types: single | double
For HNSW Searchers
Size of the candidate list of nearest neighbors for a single query
point during the search process, specified as a positive integer from
K through N. Larger values
lead to a more complete search, which increases the likelihood of
finding the true nearest neighbors, but slow the search.
SearchSetSize must be at least
K, the number of features in the data (number of
columns in Mdl.X), and must be no more than
N, the number of rows in the training data
(number of rows in Mdl.X).
Example: SearchSetSize=15
Data Types: double
Note
If you specify
'Distance',
'Cov',
'P', or
'Scale', then
Mdl.Distance and Mdl.DistParameter do
not change value.
Output Arguments
Training data indices of nearest neighbors, returned as a numeric matrix or cell array of numeric vectors.
If you do not specify
IncludeTies(falseby default), thenIdxis an m-by-k numeric matrix, where m is the number of rows inYand k is the number of searched nearest neighbors specified by the'K'name-value pair argument.Idx(j,i)indicates thatMdl.X(Idx(j,i),:)is one of the k closest observations inMdl.Xto the query observationY(j,:).If you specify
'IncludeTies',true, thenIdxis an m-by-1cell array such that cellj(Idx{j}) contains a vector of at least k indices of the closest observations inMdl.Xto the query observationY(j,:).
If SortIndices is true, then
knnsearch arranges the indices in ascending order
by distance.
Distances of the nearest neighbors to the query data, returned as a numeric matrix or cell array of numeric vectors.
If you do not specify
IncludeTies(falseby default), thenDis an m-by-k numeric matrix, where m is the number of rows inYand k is the number of searched nearest neighbors specified by the'K'name-value pair argument.D(j,i)is the distance betweenMdl.X(Idx(j,i),:)and the query observationY(j,:)with respect to the distance metric.If you specify
'IncludeTies',true, thenDis an m-by-1cell array such that cellj(D{j}) contains a vector of at least k distances of the closest observations inMdl.Xto the query observationY(j,:).
If SortIndices is true, then
knnsearch arranges the distances in ascending
order.
Tips
knnsearch finds the k (positive integer)
points in Mdl.X that are k-nearest for each
Y point. In contrast, rangesearch finds all the points in Mdl.X that are
within distance r (positive scalar) of each Y
point.
Algorithms
The values of the Distance argument that begin fast
(such as 'fasteuclidean' and 'fastseuclidean')
calculate Euclidean distances using an algorithm that uses extra memory to save
computational time. This algorithm is named "Euclidean Distance Matrix Trick" in Albanie
[1] and elsewhere. Internal
testing shows that this algorithm saves time when the number of predictors is at least 10.
Algorithms starting with 'fast' do not support sparse data.
To find the matrix D of distances between all the points xi and xj, where each xi has n variables, the algorithm computes distance using the final line in the following equations:
The matrix in the last line of the equations is called the Gram matrix. Computing the set of squared distances is faster, but slightly less numerically stable, when you compute and use the Gram matrix instead of computing the squared distances by squaring and summing. For a discussion, see Albanie [1].
References
[1] Albanie, Samuel. Euclidean Distance Matrix Trick. June, 2019. Available at https://samuelalbanie.com/files/Euclidean_distance_trick.pdf.
Alternative Functionality
knnsearchis an object function that requires anExhaustiveSearcher,KDTreeSearcher, orhnswSearchermodel object and query data. Under equivalent conditions for an exhaustive or Kd-tree search, theknnsearchobject function returns the same results as theknnsearchfunction with the specified name-value argumentNSMethod="exhaustive"orNSMethod="kdtree", respectively. Note that theknnsearchfunction does not provide a similar name-value argument for specifying anhnswSearchermodel.For k-nearest neighbors classification, see
fitcknnandClassificationKNN.
References
[1] Friedman, J. H., Bentley, J., and Finkel, R. A. (1977). “An Algorithm for Finding Best Matches in Logarithmic Expected Time.” ACM Transactions on Mathematical Software Vol. 3, Issue 3, Sept. 1977, pp. 209–226.
[2] Malkov, Yu. A., and D. A. Yashunin. Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs. Available at https://arxiv.org/abs/1603.09320.
Extended Capabilities
Usage notes and limitations:
This table contains notes about the arguments of
knnsearch. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlIf
Mdlis anhnswSearcherobject, you cannot useMdlfor code generation.There are two ways to use
Mdlin code generation. For an example, see Code Generation for Nearest Neighbor Searcher.Use
saveLearnerForCoder,loadLearnerForCoder, andcodegen(MATLAB Coder) to generate code for theknnsearchfunction. Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls theknnsearchfunction. Then usecodegento generate code for the entry-point function.Include
coder.Constant(Mdl)in the-argsvalue ofcodegen(MATLAB Coder).
If
Mdlis aKDTreeSearcherobject, and the code generation build type is a MEX function, thencodegen(MATLAB Coder) generates a MEX function using Intel® Threading Building Blocks (TBB) for parallel computation. Otherwise,codegengenerates code usingparfor(MATLAB Coder).MEX function for the kd-tree search algorithm —
codegengenerates an optimized MEX function using Intel TBB for parallel computation on multicore platforms. You can use the MEX function to accelerate MATLAB® algorithms. For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.If you generate the MEX function to test the generated code of the
parforversion, you can disable the usage of Intel TBB. Set theExtrinsicCallsproperty of the MEX configuration object tofalse. For details, seecoder.MexCodeConfig(MATLAB Coder).MEX function for the exhaustive search algorithm and standalone C/C++ code for both algorithms — The generated code of
knnsearchusesparfor(MATLAB Coder) to create loops that run in parallel on supported shared-memory multicore platforms in the generated code. If your compiler does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP library, MATLAB Coder™ treats theparfor-loops asfor-loops. To find supported compilers, see Supported Compilers. To disable OpenMP library, set theEnableOpenMPproperty of the configuration object tofalse. For details, seecoder.CodeConfig(MATLAB Coder).
'Distance'Cannot be a custom distance function.
Must be a compile-time constant; its value cannot change in the generated code.
knnsearchdoes not support code generation for fast Euclidean distance computations, meaning those distance metrics whose names begin withfast(for example,'fasteuclidean').
'IncludeTies'Must be a compile-time constant; its value cannot change in the generated code.
'SortIndices'Not supported. The output arguments are always sorted. Name-value pair arguments Names in name-value arguments must be compile-time constants. For example, to allow a user-defined exponent for the Minkowski distance in the generated code, include
{coder.Constant('Distance'),coder.Constant('Minkowski'),coder.Constant('P'),0}in the-argsvalue ofcodegen(MATLAB Coder).IdxWhen you specify
'IncludeTies'astrue, the sorted order of tied distances in the generated code can be different from the order in MATLAB due to numerical precision.knnsearchreturns integer-type (int32) indices in generated standalone C/C++ code. Therefore, the function allows for strict single-precision support when you use single-precision inputs. For MEX code generation, the function still returns double-precision indices to match the MATLAB behavior.
For more information, see Introduction to Code Generation and Code Generation for Nearest Neighbor Searcher.
Version History
Introduced in R2010aFind approximate nearest neighbors using an hnswSearcher model
object. An hnswSearcher object takes longer to create than an
ExhaustiveSearcher or KDTreeSearcher
object, but computes approximate nearest neighbors more quickly. Create an
hnswSearcher object by using the
hnswSearcher function or by using createns with the specification NSMethod="hnsw".
For details, see hnswSearcher.
The 'fasteuclidean' and 'fastseuclidean'
distance metrics accelerate the computation of Euclidean distances by using a cache
and a different algorithm (see Algorithms).
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)