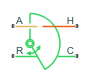
Rotational Mechanical Converter (TL)
Interface between thermal liquid and mechanical rotational networks
Libraries:
Simscape /
Foundation Library /
Thermal Liquid /
Elements
Description
The Rotational Mechanical Converter (TL) block models an interface between a thermal liquid network and a mechanical rotational network. The block converts thermal liquid pressure into mechanical torque and vice versa. It can be used as a building block for rotary actuators.
The converter contains a variable volume of liquid. The temperature evolves based on the thermal capacity of this volume. If the Enable dynamic compressibility check box is selected, then the pressure also evolves based on the dynamic compressibility of the liquid volume. The Mechanical orientation parameter lets you specify whether an increase in the liquid volume results in a positive or negative rotation of port R relative to port C.
Port A is the thermal liquid conserving port associated with the converter inlet. Port H is the thermal conserving port associated with the temperature of the liquid inside the converter. Ports R and C are the mechanical rotational conserving ports associated with the moving interface and converter casing, respectively.
Mass Balance
The mass conservation equation in the mechanical converter volume is
where:
is the liquid mass flow rate into the converter through port A.
ε is the mechanical orientation of the converter (
1if increase in fluid pressure causes positive rotation of R relative to C,-1if increase in fluid pressure causes negative rotation of R relative to C).ρ is the liquid mass density.
D is the converter displacement.
Ω is the angular velocity of the converter interface.
V is the liquid volume inside the converter.
β is the liquid bulk modulus inside the converter.
α is the coefficient of thermal expansion of the liquid.
p is the liquid pressure inside the converter.
T is the liquid temperature inside the converter.
If you connect the converter to a Multibody joint, use the physical signal input port q to specify the rotation of port R relative to port C. Otherwise, the block calculates the interface rotation from relative port angular velocities, according to the block equations. The interface rotation is zero when the liquid volume is equal to the dead volume. Then, depending on the Mechanical orientation parameter value:
If
Pressure at A causes positive rotation of R relative to C, the interface rotation increases when the liquid volume increases from dead volume.If
Pressure at A causes negative rotation of R relative to C, the interface rotation decreases when the liquid volume increases from dead volume.
Momentum Balance
The momentum conservation equation in the mechanical converter volume is
where:
τ is the torque the liquid exerts on the converter interface.
pAtm is the atmospheric pressure.
Energy Balance
The energy conservation equation in the mechanical converter volume is
where:
u is the liquid internal energy in the converter.
ϕA is the total energy flow rate into the mechanical converter volume through port A.
QH is the heat flow rate into the mechanical converter volume.
Assumptions and Limitations
Converter walls are not compliant. They cannot deform regardless of internal pressure and temperature.
The converter contains no mechanical hard stops. To include hard stops, use the Rotational Hard Stop block.
The flow resistance between the inlet and the interior of the converter is negligible.
The thermal resistance between the thermal port and the interior of the converter is negligible.
The kinetic energy of the fluid in the converter is negligible.
Ports
Input
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2013b