잡음 내 지연된 신호의 상호상관

이 예제에서는 상호상관 시퀀스를 사용하여 잡음으로 인해 손상된 시퀀스에서 시간 지연을 감지하는 방법을 보여줍니다. 출력 시퀀스는 입력 시퀀스가 지연된 것으로, 가산성 백색 가우스 잡음(AWGN)이 포함되어 있습니다. 2개의 시퀀스를 만듭니다. 한 시퀀스는 다른 시퀀스가 지연된 것입니다. 3개 샘플이 지연되었습니다. $$N(0,0.3^2)$$ 백색 잡음을 지연된 신호에 추가합니다. 샘플 상호상관 시퀀스를 사용하여 지연을 감지합니다.

신호를 만들고 플로팅합니다. 재현 가능한 결과를 얻기 위해 난수 생성기를 디폴트 설정으로 구성합니다.

rng default

x = triang(20);
y = [zeros(3,1);x]+0.3*randn(length(x)+3,1);

subplot(2,1,1)
stem(x,'filled')
axis([0 22 -1 2])
title('Input Sequence')

subplot(2,1,2)
stem(y,'filled')
axis([0 22 -1 2])
title('Output Sequence')

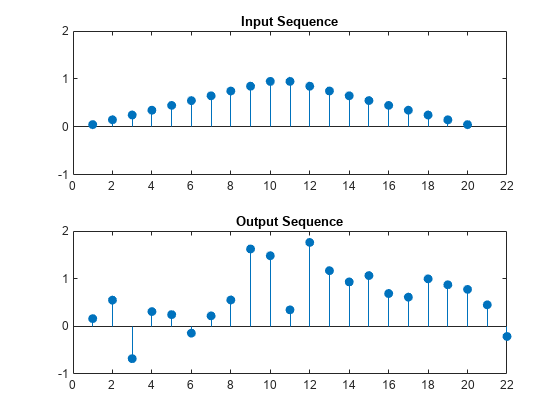
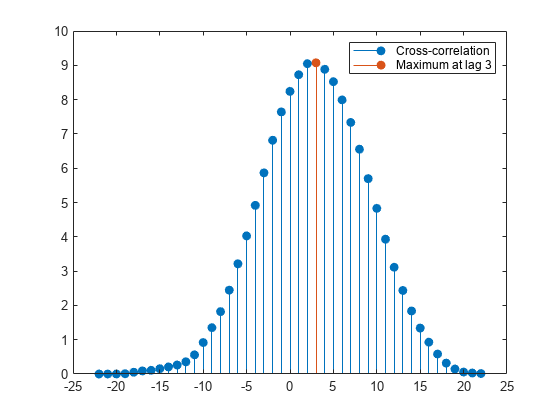
샘플 상호상관 시퀀스를 가져오고 최대 절댓값을 사용하여 지연을 측정합니다. 샘플 상호상관 시퀀스를 플로팅합니다. 예상대로 지연값 3에서 최대 상호상관 시퀀스 값이 발생합니다.

[xc,lags] = xcorr(y,x);
[~,I] = max(abs(xc));

figure
stem(lags,xc,'filled')
hold on
stem(lags(I),xc(I),'filled')
hold off
legend(["Cross-correlation",sprintf('Maximum at lag %d',lags(I))])

finddelay 함수를 사용하여 결과를 확인합니다.

finddelay(x,y)

ans = 
3

참고 항목

finddelay | xcorr