표본 자기상관에 대한 신뢰구간
이 예제에서는 백색 잡음 과정의 자기상관 시퀀스에 대한 신뢰구간을 만드는 방법을 보여줍니다. 길이 인 샘플을 사용하여 백색 잡음 과정에 대한 구현을 생성합니다. 지연값 20까지 표본 자기상관을 구합니다. 백색 잡음 과정의 표본 자기상관을 약 95% 신뢰구간과 함께 플로팅합니다.
백색 잡음 확률 벡터를 만듭니다. 재현 가능한 결과를 얻기 위해 난수 생성기를 디폴트 설정으로 구성합니다. 지연값 20까지 정규화된 표본 자기상관을 구합니다.
rng default L = 1000; x = randn(L,1); [xc,lags] = xcorr(x,20,'coeff');
표준편차가 인 정규분포 에 대한 95% 신뢰 하한 및 상한을 만듭니다. 95% 신뢰구간에서 임계값은 이고 신뢰구간은 다음과 같습니다.
vcrit = sqrt(2)*erfinv(0.95)
vcrit = 1.9600
lconf = -vcrit/sqrt(L); upconf = vcrit/sqrt(L);
표본 자기상관을 95% 신뢰구간과 함께 플로팅합니다.
stem(lags,xc,'filled') hold on plot(lags,[lconf;upconf]*ones(size(lags)),'r') hold off ylim([lconf-0.03 1.05]) title('Sample Autocorrelation with 95% Confidence Intervals')
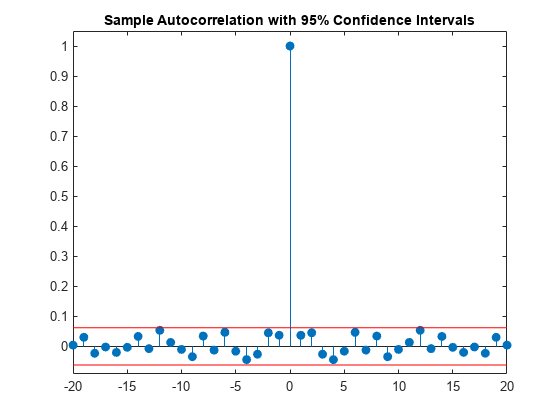
위 그림을 보면, 유일하게 95% 신뢰구간 바깥에 있는 자기상관 값은 지연값 0에서 발생한 것을 알 수 있으며, 이는 백색 잡음 과정에 대해 예상되는 결과입니다. 이 결과에 근거하여 이 데이터가 백색 잡음 과정을 구현한 것이라고 결론을 내릴 수 있습니다.