이 번역 페이지는 최신 내용을 담고 있지 않습니다. 최신 내용을 영문으로 보려면 여기를 클릭하십시오.

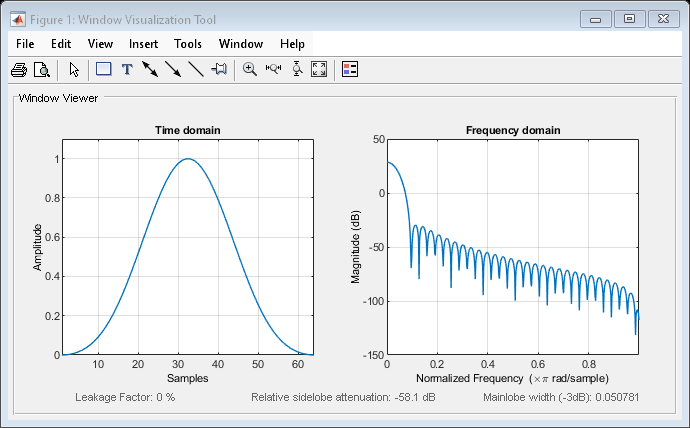
blackman

블랙맨 윈도우

구문

w = blackman(L)

w = blackman(L,sflag)

설명

w = blackman(L)은 L개 점을 갖는 대칭형 블랙맨 윈도우를 반환합니다.

w = blackman(L,sflag)는 sflag로 지정된 윈도우 샘플링 방법을 사용하여 블랙맨 윈도우를 반환합니다.

예제

블랙맨 윈도우

64개 점을 갖는 블랙맨 윈도우를 생성합니다. wvtool을 사용하여 결과를 표시합니다.

L = 64;
wvtool(blackman(L))

입력 인수

L — 윈도우 길이

양의 정수

윈도우 길이로, 양의 정수로 지정됩니다.

데이터형: single | double

sflag — 윈도우 샘플링

'symmetric' (디폴트 값) | 'periodic'

윈도우 샘플링 방법으로, 다음과 같이 지정됩니다.

• 'symmetric' — 필터 설계에 윈도우를 사용할 경우 이 옵션을 사용합니다.

• 'periodic' — 이 옵션은 윈도우가 적용된 신호가 이산 푸리에 변환에서 묵시적인 완벽한 주기적 확장을 이루도록 하기 때문에, 스펙트럼 분석에 유용합니다. 'periodic'이 지정되면 이 함수는 길이가 L + 1인 윈도우를 계산하고 처음 L개 점을 반환합니다.

출력 인수

w — 블랙맨 윈도우

열 벡터

블랙맨 윈도우로, 열 벡터로 반환됩니다.

알고리즘

다음 방정식은 길이가 N인 블랙맨 윈도우를 정의합니다.

$$w(n)=0.42-0.5\cos \left(\frac{2\pi n}{L-1}\right)+0.08\cos \left(\frac{4\pi n}{L-1}\right),0\le n\le M-1$$

여기서 M은 N이 짝수인 경우 N/2이고 N이 홀수인 경우 (N + 1)/2입니다.

대칭형인 경우, 블랙맨 윈도우의 두 번째 절반 M ≤ n ≤ N – 1은 중간점을 기준으로 첫 번째 절반에 대해 대칭 이동을 수행하는 방식으로 구합니다. FIR 필터 설계에 블랙맨 윈도우를 사용하는 경우 대칭형 옵션을 사용하는 것이 좋습니다.

주기적 블랙맨 윈도우는 원하는 윈도우 길이를 한 개 샘플만큼 늘려 N + 1로 키워 대칭형 윈도우를 생성한 후 마지막 샘플을 제거하는 방식으로 생성됩니다. 이산 푸리에 변환은 입력 벡터의 주기적 확장을 가정하므로 스펙트럼 분석에서 블랙맨 윈도우를 사용하는 경우 주기적 버전을 사용하는 것이 좋습니다.

참고 문헌

[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, pp. 468–471.

확장 기능

C/C++ 코드 생성
MATLAB® Coder™를 사용하여 C 코드나 C++ 코드를 생성할 수 있습니다.

GPU 코드 생성
GPU Coder™를 사용하여 NVIDIA® GPU용 CUDA® 코드를 생성할 수 있습니다.

버전 내역

R2006a 이전에 개발됨

R2024a: blackman가 GPU 코드 생성을 지원함

blackman 함수는 GPU(그래픽 처리 장치)에 대한 코드 생성을 지원합니다. CUDA^® 코드를 생성하려면 MATLAB^® Coder™와 GPU Coder™가 필요합니다.

참고 항목

앱

• 윈도우 디자이너

함수

• flattopwin | hamming | hann | WVTool