Generic Engine
Generic internal combustion engine
Libraries:
Simscape /
Driveline /
Engines & Motors
Description
The Generic Engine block represents a configurable internal combustion engine that is suitable for spark-ignition and diesel applications. You can control the block using either a torque or normalized throttle physical signal. You can parameterize the block by using a third-order polynomial or by using tabulated torque or power data. Optional dynamic parameters include crankshaft inertia and response time lag. A physical signal port, FC, outputs the engine fuel consumption rate based on the fuel consumption model that you choose. Optional speed and redline controllers prevent engine stall and enable cruise control. The figure shows how the ports relate to an engine configuration.

Engine Speed, Throttle, Power, and Torque
By default, the Generic Engine block uses a programmed relationship between torque and speed that the throttle signal or the torque command signal modulates.
The block evaluates engine power demand as a function of engine speed, g(ɷ). The function provides the maximum power available for a given engine speed, ɷ. The block parameters Maximum power, Speed at maximum power, and Maximum speed normalize this function to physical maximum torque and speed values.
The normalized throttle signal, Thr, controls the engine power such that P(ɷ,Thr) =
Thr·g(ɷ). When you set Model parameterization to
Normalized throttle, the physical input signal
Thr controls the engine power. When you choose
Torque command, the block computes the normalized
throttle internally. The block delivers power as a fraction of the maximum power
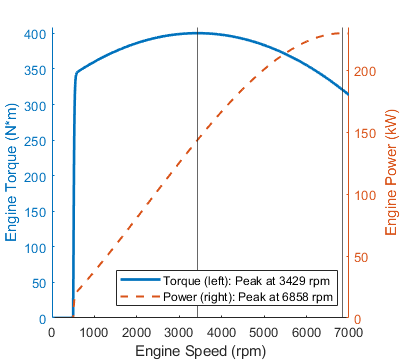
possible in a steady state at a fixed engine speed. The figure shows the torque and
power curves for the default settings.
Note that the torque available at port F during
transients may differ from the value of the logged variable, trq.
The logged variable tracks the torque produced and does not account for torque lost
to system inertia.
Polynomial Engine Control
When you set Model parameterization to
Normalized 3rd-order polynomial, the block uses the
normalized engine speed, ɷN, to compute
the speed and torque. The block defines the normalized engine speed as
where:
ɷ is the current engine speed.
ɷPP is the engine speed at peak power.
The block treats the normalized, dimensionless engine power as a third-order polynomial such that
where s1, s2, and s3 are constant polynomial coefficients and Pp is the peak power. In typical engines, the si coefficients are positive.
The block calculates engine torque at the wide-open throttle condition using the polynomial coefficients such that
The block sets the normalized engine speed at peak power such that
Substituting this equality into the formula for pN gives
This condition normalizes the power to the engine speed at peak power. The block sets the slope of pN(ɷPP) to zero, such that
The block defines the normalized engine speed of peak torque as
where the speed of peak power is greater than the speed of peak torque. The block uses the polynomial formulation to find the dimensionless, normalized torque, τN, and to sets the slope to zero such that
Solving for si using these equations yields
The block calculates the engine torque as
where TP is the peak torque. Substituting the equation for ɷNPT yields the constraint
The block uses TP, PP, and ɷPT to calculate the engine speed at peak power such that
where TPɷPT is equivalent to the power at peak torque, PPT, which is always less than the peak power, PP.
The block calculates the polynomial using the corresponding coefficients for the setting
of the Engine type parameter. When you set Engine
type to Spark-ignition or
Diesel, the block selects the appropriate
coefficients from the table. When you select Generic,
the block computes these coefficients internally.
| Power Demand Coefficient | Engine Type | |
|---|---|---|
| Spark-Ignition | Diesel | |
| s1 | 1 | 0.6526 |
| s2 | 1 | 1.6948 |
| s 3 | -1 | -1.3474 |
Fuel Consumption
The block can optionally model fuel consumption and output the results as a physical signal at port FC. To include fuel consumption in your simulation, set Fuel consumption model to one of these settings:
Constant per revolutionFuel consumption by speed and torqueBrake specific fuel consumption by speed and torqueBrake specific fuel consumption by speed and brake mean effective pressure
You can create a visual representation of the fuel consumption. When
you set Fuel consumption model to Fuel consumption
by speed and torque and click the engine
properties hyperlink in the block description, a live script
generates a heat map plot of fuel consumption for a given torque and speed.
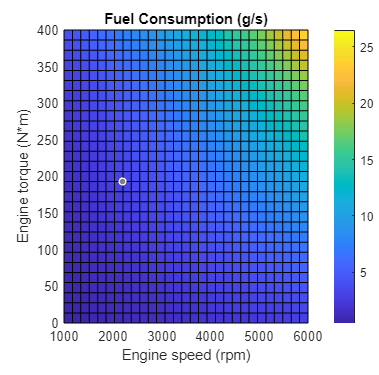
This plot is in addition to the engine speed, throttle, power and
torque plot. When you set Fuel consumption model to
Brake specific fuel consumption by speed and torque
or Brake specific fuel consumption by speed and brake mean effective
pressure, the live script generates the heat map plot of fuel
consumption and a separate plot for brake-specific fuel consumption.

Idle Speed Controller Model
The idle speed controller adjusts the throttle signal to increase engine rotation below a reference speed according to:
and
where:
Π is the engine throttle.
Πi is the input throttle port Thr.
Πc is the controller throttle.
ω is the engine speed or crankshaft angular velocity.
ωr is the idle speed reference.
ωt is the controller speed threshold.
τ is the controller time constant.
The controlled throttle increases with a first-order lag from 0 to 1 when engine speed falls below the reference speed. When the engine speed rises above the reference speed, the controlled throttle decreases from one to zero. When the difference between engine velocity and reference speed is smaller than the controller speed threshold, the tanh part of the equation smooths the time derivative of the controlled throttle. The smoothing function limits the controlled throttle to the range [0,1]. The engine uses the larger of the input and controlled throttle values. If you include engine time lag, the controller changes the input before it computes the lag.
Redline Controller Model
The idle speed controller determines the minimum throttle value for maintaining engine speed, the redline controller prevents excessive speed based on a maximum throttle input. To determine the maximum throttle value, the redline controller uses the idle speed controller model equation. However, for the redline controller:
ωr is the redline speed reference.
ωt is the redline speed threshold.
τ is the redline time constant.
Performance
To increase simulation speed, set Fuel consumption model to
No fuel consumption. When you use this setting, the
block does not calculate fuel consumption regardless of port
FC.
If you select any other option for Fuel consumption model, the block must perform a nonlinear computation. The block solves the equation even if the FC port, which reports the fuel consumption rate, is not connected to another block.
Predefined Parameterization
You can populate the block with pre-parameterized manufacturing data, which allows you to model a specific supplier component.
To load a predefined parameterization:
In the block dialog box, next to Selected part, click the "<click to select>" hyperlink next to Selected part in the block dialog box settings.
The Block Parameterization Manager window opens. Select a part from the menu and click Apply all. You can narrow the choices using the Manufacturer drop down menu.
You can close the Block Parameterization Manager menu. The block now has the parameterization that you specified.
You can compare current parameter settings with a specific supplier component in the Block Parameterization Manager window by selecting a part and viewing the data in the Compare selected part with block section.
Note
Predefined block parameterizations use available data sources to supply parameter values. The block substitutes engineering judgment and simplifying assumptions for missing data. As a result, expect some deviation between simulated and actual physical behavior. To ensure accuracy, validate the simulated behavior against experimental data and refine your component models as necessary.
Assumptions and Limitations
Engines lag in their response to changing speed and throttle. The block supports lag due to a changing throttle only.
Hardware-in-the-Loop Simulation
To improve performance for HIL simulation, set the Dynamics > Time Constant parameter to No time constant - Suitable for HIL
simulation.
Examples
Ports
Input
Output
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2011a