Particle Filter Workflow
A particle filter is a recursive, Bayesian state estimator that uses discrete particles to approximate the posterior distribution of the estimated state.
The particle filter algorithm computes the state estimate recursively and involves two steps:
Prediction – The algorithm uses the previous state to predict the current state based on a given system model.
Correction – The algorithm uses the current sensor measurement to correct the state estimate.
The algorithm also periodically redistributes, or resamples, the particles in the state space to match the posterior distribution of the estimated state.
The estimated state consists of all the state variables. Each particle represents a discrete state hypothesis. The set of all particles is used to help determine the final state estimate.
You can apply the particle filter to arbitrary nonlinear system models. Process and measurement noise can follow arbitrary non-Gaussian distributions.
To use the particle filter properly, you must specify parameters such as the number of particles, the initial particle location, and the state estimation method. Also, if you have a specific motion and sensor model, you specify these parameters in the state transition function and measurement likelihood function, respectively. For more information, see Particle Filter Parameters.
Follow this basic workflow to create and use a particle filter. This page details the estimation workflow and shows an example of how to run a particle filter in a loop to continuously estimate state.
Estimation Workflow
When using a particle filter, there is a required set of steps to create the particle filter and estimate state. The prediction and correction steps are the main iteration steps for continuously estimating state.
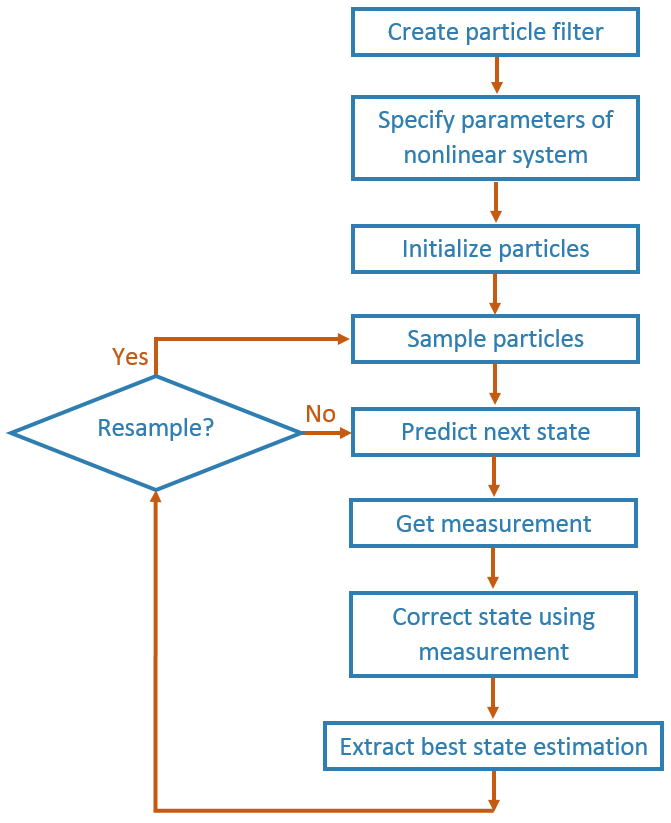
Create Particle Filter
Create a stateEstimatorPF object.
Set Parameters of Nonlinear System
Modify these stateEstimatorPF parameters to fit for your specific system or application:
StateTransitionFcnMeasurementLikelihoodFcnResamplingPolicyResamplingMethodStateEstimationMethod
Default values for these parameters are given for basic operation.
The StateTransitionFcn and MeasurementLikelihoodFcn
functions define the system behavior and measurement integration. They are vital for
the particle filter to track accurately. For more information, see Particle Filter Parameters.
Initialize Particles
Use the initialize function to set the number of particles and the initial
state.
Sample Particles from a Distribution
You can sample the initial particle locations in two ways:
Initial pose and covariance — If you have an idea of your initial state, it is recommended you specify the initial pose and covariance. This specification helps to cluster particles closer to your estimate so tracking is more effective from the start.
State bounds — If you do not know your initial state, you can specify the possible limits of each state variable. Particles are uniformly distributed across the state bounds for each variable. Widely distributed particles are not as effective at tracking, because fewer particles are near the actual state. Using state bounds usually requires more particles, computation time, and iterations to converge to the actual state estimate.
Predict
Based on a specified state transition function, particles evolve to estimate the next state.
Use predict
to execute the state transition function specified in the
StateTransitionFcn property.
Get Measurement
The measurements collected from sensors are used in the next step to correct the current predicted state.
Correct
Measurements are then used to adjust the predicted state and correct the estimate. Specify
your measurements using the correct function. correct uses the
MeasurementLikelihoodFcn to calculate the likelihood of
sensor measurements for each particle. Resampling of particles is required to update
your estimation as the state changes in subsequent iterations. This step triggers
resampling based on the ResamplingMethod and
ResamplingPolicy properties.
Extract Best State Estimation
After calling correct, the best state estimate is automatically extracted
based on the Weights of each particle and the
StateEstimationMethod property specified in the object. The
best estimated state and covariance is output by the correct
function.
Resample Particles
This step is not separately called, but is executed when you
call correct. Once your state has changed enough,
resample your particles based on the newest estimate. The correct method
checks the ResamplingPolicy for the triggering
of particle resampling according to the current distribution of particles
and their weights. If resampling is not triggered, the same particles
are used for the next estimation. If your state does not vary by much
or if your time step is low, you can call the predict and correct
methods without resampling.
Continuously Predict and Correct
Repeat the previous prediction and correction steps as needed
for estimating state. The correction step determines if resampling
of the particles is required. Multiple calls for predict or correct might
be required when:
No measurement is available but control inputs and time updates are occur at a high frequency. Use the
predictmethod to evolve the particles to get the updated predicted state more often.Multiple measurement reading are available. Use
correctto integrate multiple readings from the same or multiple sensors. The function corrects the state based on each set of information collected.
See Also
stateEstimatorPF | initialize | getStateEstimate | predict | correct