Find Image Peaks and Valleys

You can think of a grayscale image as a three-dimensional object, with the x- and y-axes representing pixel positions and the z-axis representing the intensity of each pixel. In this interpretation, the intensity values represent elevations, as in a topographical map. The areas of high intensity and low intensity in an image, respectively peaks and valleys in topographical terms, can be important morphological features because they often mark relevant image objects.

For example, in an image of several spherical objects, points of high intensity can represent the tops of the objects. Using morphological processing, you can use these maxima to identify objects in an image.

Global and Regional Minima and Maxima

This table defines the terminology used to describe peaks and valleys in images.

Term	Definition
Global maximum	Highest regional maximum in the image.
Global minimum	Lowest regional minimum in the image.
Regional maxima	Each of the regional maxima in the image is a connected set of pixels in which all pixels have the same intensity value, t, surrounded by pixels that all have an intensity value less than t.
Regional minima	Each of the regional minima in the image is a connected set of pixels in which all pixels have the same intensity value, t, surrounded by pixels that all have an intensity value greater than t.

An image can have multiple regional minima or maxima, but typically has only one global minimum and maximum. However, if multiple regional minima or maxima share the same extreme value, then an image can have multiple global minima or maxima.

This figure illustrates the concept of global and regional minima and maxima in 1-D.

Find Areas of High or Low Intensity

The toolbox includes functions that you can use to find areas of high or low intensity in an image:

• The imregionalmax and imregionalmin functions identify all regional minima or maxima.

• The imextendedmax and imextendedmin functions identify regional minima or maxima that are greater than or less than a specified threshold.

The functions accept a grayscale image as input and return a binary image as output. In the output binary image, the regional minima or maxima are set to 1, while all other pixels are set to 0.

For example, this image A contains two primary regional maxima, the blocks of pixels containing the values 14 and 18. It also contains several smaller maxima, with values of 11.

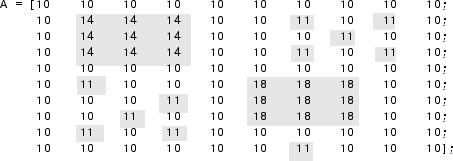
The binary image returned by imregionalmax pinpoints all these regional maxima.

B = imregionalmax(A)

If you want to identify only the areas of the image where the change in intensity is greater than or less than a certain threshold, use the imextendedmax and imextendedmin functions. For example, to find only those regional maxima in the sample image A that are at least two units higher than their neighbors, enter this command.

B = imextendedmax(A,2)

Suppress Minima and Maxima

In an image, every small fluctuation in intensity represents a regional minimum or maximum. If you are interested in only significant minima or maxima, and not in these smaller minima and maxima caused by background texture, you can remove only the less significant minima and maxima but retain the significant minima and maxima by using the imhmax and imhmin functions. Use these functions to specify a threshold level, h, that suppresses all maxima with height less than h or minima with height greater than h.

Note

The imregionalmin, imregionalmax, imextendedmin, and imextendedmax functions return a binary image that indicates the locations of the regional minima and maxima in an image. The imhmax and imhmin functions return an altered image of the same size and data type as the input image.

For example, consider again image A.

To eliminate all regional maxima except the two significant maxima, use imhmax with a threshold value of 2. Note that imhmax affects only the maxima without changing any of the other pixel values. The two significant maxima remain, but their heights are reduced.

B = imhmax(A,2)

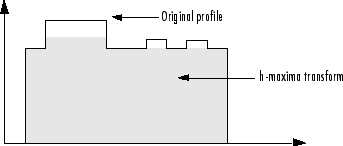
Notice that, in the original image, the second row has one significant regional maximum and two smaller regional maxima. The imhmax function reduces the value of each maximum by 2, retaining only the maximum with an adjusted value greater than that of the surrounding pixels. This figure illustrates the process in 1-D.

Impose a Minimum

You can emphasize specific minima in an image by using the imimposemin function. The imimposemin function uses morphological reconstruction to eliminate all minima from the image except the minima you specify.

Consider an image that contains two primary regional minima and several other regional minima.

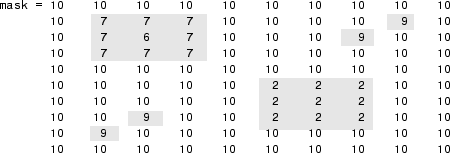
To obtain an image that emphasizes the two deepest minima and removes all others, create a marker image that pinpoints the two minima of interest. You can create the marker image by explicitly setting certain pixels to specific values, or by using other morphological functions to extract the features you want to emphasize in the mask image.

This example uses imextendedmin to get a binary image that shows the locations of the two deepest minima.

marker = imextendedmin(mask,1)

Use imimposemin to create new minima in the mask image at the points specified by the marker image. Note how imimposemin sets the values of pixels specified by the marker image to the lowest value supported by the data type (0 for uint8 values). imimposemin also changes the values of all the other pixels in the image to eliminate the other minima.

I = imimposemin(mask,marker)

I =
    11    11    11    11    11    11    11    11    11    11
    11     8     8     8    11    11    11    11    11    11
    11     8     0     8    11    11    11    11    11    11
    11     8     8     8    11    11    11    11    11    11
    11    11    11    11    11    11    11    11    11    11
    11    11    11    11    11     0     0     0    11    11
    11    11    11    11    11     0     0     0    11    11
    11    11    11    11    11     0     0     0    11    11
    11    11    11    11    11    11    11    11    11    11
    11    11    11    11    11    11    11    11    11    11

This figure illustrates in 1-D how imimposemin changes the profile of the third row of the image. After minima imposition, the final image profile has one minimum at the location of the marker image profile minimum.