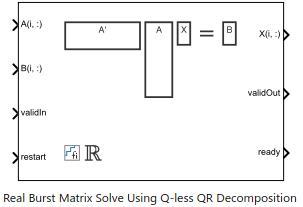
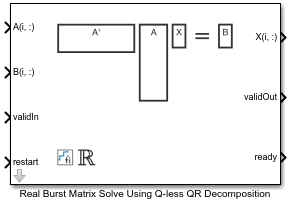
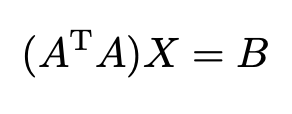Real Burst Matrix Solve Using Q-less QR Decomposition
Compute the value of X in the equation A'AX = B for real-valued matrices using Q-less QR decomposition
Libraries:
Fixed-Point Designer HDL Support /
Matrices and Linear Algebra /
Linear System Solvers
Description
The Real Burst Matrix Solve Using Q-less QR Decomposition block solves the system of linear equations A'AX = B using Q-less QR decomposition, where A and B are real-valued matrices.
When Regularization parameter is nonzero, the Real Burst Matrix Solve Using Q-less QR Decomposition block solves the matrix equation
where λ is the regularization parameter,
A is an m-by-n matrix, and
In =
eye(n).
Examples
Implement Hardware-Efficient Real Burst Matrix Solve Using Q-less QR Decomposition
How to use the Real Burst Matrix Solve Using Q-less QR Decomposition block.
Implement Hardware-Efficient Real Burst Matrix Solve Using Q-less QR Decomposition with Tikhonov Regularization
Use the Real Burst Matrix Solve Using QR Decomposition block to solve the regularized least-squares matrix equation
Algorithms to Determine Fixed-Point Types for Real Q-less QR Matrix Solve A'AX=B
Derivation of algorithms for determining fixed-point types for real Q-less QR matrix solve.
Determine Fixed-Point Types for Real Q-less QR Matrix Solve A'AX=B
Use fixed.realQlessQRFixedpointTypes to determine fixed-point types
for computation of the real least-squares matrix equation.
Determine Fixed-Point Types for Real Q-less QR Matrix Solve with Tikhonov Regularization
Use the fixed.realQlessQRMatrixSolveFixedpointTypes function to analytically determine fixed-point types for the solution of the real least-squares matrix equation
Ports
Input
Rows of real matrix A, specified as a vector. A is an m-by-n matrix where m ≥ 2 and m ≥ n. If B is single or double, A must be the same data type as B. If A is a fixed-point data type, A must be signed, use binary-point scaling, and have the same word length as B. Slope-bias representation is not supported for fixed-point data types.
Data Types: single | double | fixed point
Rows of real matrix B, specified as a vector. B is an n-by-p matrix where n ≥ 2. If A is single or double, B must be the same data type as A. If B is a fixed-point data type, B must be signed, use binary-point scaling, and have the same word length as A. Slope-bias representation is not supported for fixed-point data types.
Data Types: single | double | fixed point
Whether inputs are valid, specified as a Boolean scalar. This control signal
indicates when the data from the A(i,:) and
B(i,:) input ports are valid. When this value is
1 (true) and the value at
ready is 1 (true), the
block captures the values at the A(i,:) and
B(i,:) input ports. When this value is 0
(false), the block ignores the input samples.
After sending a true
validIn signal, there may be some delay before
ready is set to false. To ensure all data is
processed, you must wait until ready is set to
false before sending another true
validIn signal.
Data Types: Boolean
Whether to clear internal states, specified as a Boolean scalar. When this value
is 1 (true), the block stops the current calculation and clears all
internal states. When this value is 0 (false) and the
validIn value is 1 (true), the block begins
a new subframe.
Data Types: Boolean
Output
Rows of the matrix X, returned as a scalar or vector.
Data Types: single | double | fixed point
Whether the output data is valid, returned as a Boolean scalar. This control
signal indicates when the data at the output port X(i,:) is
valid. When this value is 1 (true), the block
has successfully computed a row of X. When this value is
0 (false), the output data is not
valid.
Data Types: Boolean
Whether the block is ready, returned as a Boolean scalar. This control signal
indicates when the block is ready for new input data. When this value is
1 (true) and the validIn
value is 1 (true), the block accepts input data
in the next time step. When this value is 0
(false), the block ignores input data in the next time
step.
After sending a true
validIn signal, there may be some delay before
ready is set to false. To ensure all data is
processed, you must wait until ready is set to
false before sending another true
validIn signal.
Data Types: Boolean
Parameters
Number of rows in matrix A, specified as a positive integer-valued scalar.
Programmatic Use
Block Parameter:
m |
| Type: character vector |
| Values: positive integer-valued scalar |
Default:
4 |
Number of columns in matrix A and rows in matrix B, specified as a positive integer-valued scalar.
Programmatic Use
Block Parameter:
n |
| Type: character vector |
| Values: positive integer-valued scalar |
Default:
4 |
Number of columns in matrix B, specified as a positive integer-valued scalar.
Programmatic Use
Block Parameter:
p |
| Type: character vector |
| Values: positive integer-valued scalar |
Default:
1 |
Regularization parameter, specified as a nonnegative scalar. Small, positive values of the regularization parameter can improve the conditioning of the problem and reduce the variance of the estimates. While biased, the reduced variance of the estimate often results in a smaller mean squared error when compared to least-squares estimates.
Programmatic Use
Block Parameter:
regularizationParameter |
| Type: character vector |
| Values: real nonnegative scalar |
Default:
0 |
Data type of the output matrix X, specified as
fixdt(1,18,14), double,
single, fixdt(1,16,0), or as a user-specified
data type expression. The type can be specified directly, or expressed as a data type
object such as Simulink.NumericType.
Programmatic Use
Block Parameter:
OutputType |
| Type: character vector |
Values:
'fixdt(1,18,14)' | 'double' |
'single' | 'fixdt(1,16,0)' |
'<data type expression>' |
Default:
'fixdt(1,18,14)' |
Tips
Use fixed.getQlessQRMatrixSolveModel(A,B) to generate a template model
containing a Real Burst Matrix Solve Using Q-less QR Decomposition block for
real-valued input matrices A and B.
Algorithms
Systolic implementations prioritize speed of computations over space constraints, while burst implementations prioritize space constraints at the expense of speed of the operations. The following table illustrates the tradeoffs between the implementations available for matrix decompositions and solving systems of linear equations.
| Implementation | Throughput | Latency | Area |
|---|---|---|---|
| Systolic | C | O(n) | O(mn2) |
| Partial-Systolic | C | O(m) | O(n2) |
| Partial-Systolic with Forgetting Factor | C | O(n) | O(n2) |
| Burst | O(n) | O(mn) | O(n) |
Where C is a constant proportional to the word length of the data, m is the number of rows in matrix A, and n is the number of columns in matrix A.
For additional considerations in selecting a block for your application, see Choose a Block for HDL-Optimized Fixed-Point Matrix Operations.
The Matrix Solve Using QR Decomposition blocks operate synchronously. These blocks first decompose the input A and B matrices into R and C matrices using a QR decomposition block. Then, a back substitute block computes RX = C. The input A and B matrices propagate through the system in parallel, in a synchronized way.
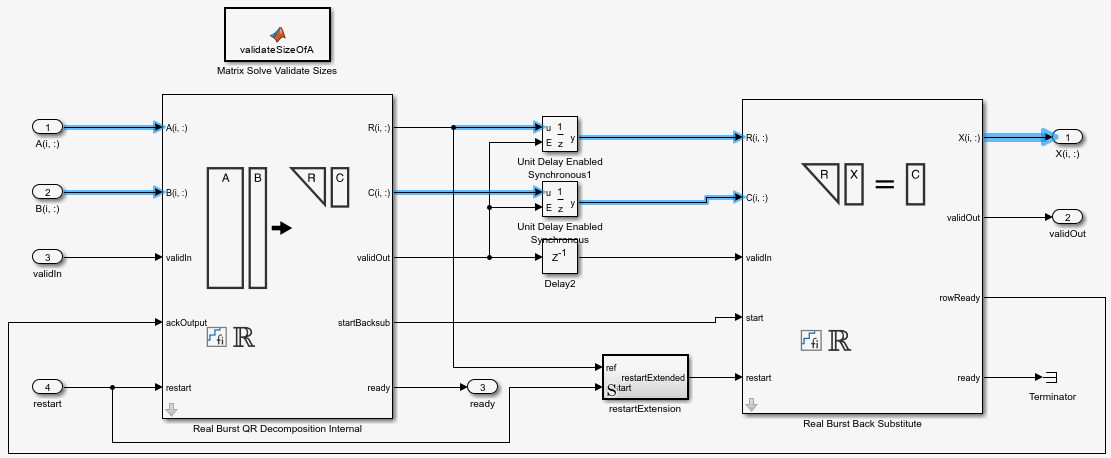
The Matrix Solve Using Q-less QR Decomposition blocks operate asynchronously. First, Q-less QR decomposition is performed on the input A matrix and the resulting R matrix is put into a buffer. Then, a forward backward substitution block uses the input B matrix and the buffered R matrix to compute R'RX = B. Because the R and B matrices are stored separately in buffers, the upstream Q-less QR decomposition block and the downstream Forward Backward Substitute block can run independently. The Forward Backward Substitute block starts processing when the first R and B matrices are available. Then it runs continuously using the latest buffered R and B matrices, regardless of the status of the Q-less QR Decomposition block. For example, if the upstream block stops providing A and B matrices, the Forward Backward Substitute block continues to generate the same output using the last pair of R and B matrices.

The Burst (Asynchronous) Matrix Solve Using Q-less QR Decomposition blocks are available in both synchronous and asynchronous operation variants, as denoted by the block name.
This block uses the AMBA AXI handshake protocol [1]. The valid/ready handshake process is used to transfer data and control information. This two-way control mechanism allows both the manager and subordinate to control the rate at which information moves between manager and subordinate. A valid signal indicates when data is available. The ready signal indicates that the block can accept the data. Transfer of data occurs only when both the valid and ready signals are high.
The Burst Matrix Solve Using Q-less QR Decomposition blocks accept and process A and B matrices row by row synchronously. After accepting m rows, the block outputs the X matrix row by row continuously. The matrix is output from the first row to the last row.
For example, assume that the input A and B
matrices are 3-by-3. Additionally assume that validIn asserts before
ready, meaning that the upstream data source is faster than the QR
decomposition.
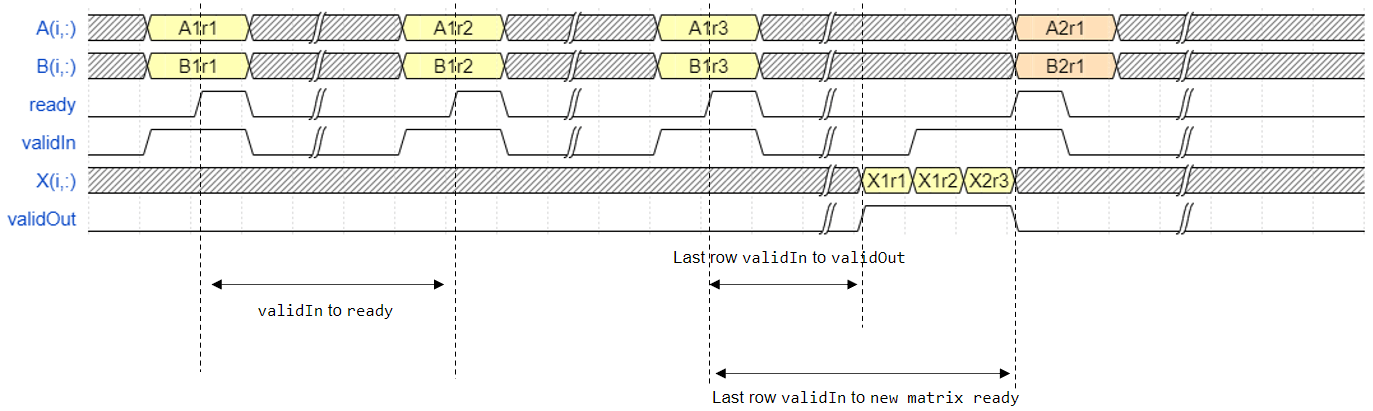
In the figure,
A1r1is the first row of the first A matrix,X1r3is the third row of the first X matrix, and so on.validIntoready— From a successful row input to the block being ready to accept the next row within one matrix.Last row
validIntovalidOut— From the last row input to the block starting to output the solution.Last row
validInto new matrix ready — From the block starting to output the solution to the block ready to accept the next matrix input.
The following table provides details of the timing for the Real Burst Matrix Solve Using Q-less QR Decomposition block. Latency depends on the size of matrix A and the data types of the A and B matrices. In the table:
In the table, m represents the number of rows in matrix A, and n is the number of columns in matrix A. wl represents the word length of the input data.
m is the number of rows in matrix A.
n is the number of columns in matrix A.
wl represents the word length of the input data in matrix A.
| Input Data Type | validIn to ready (cycles) | Last Row validIn to validOut
(cycles) | Last row validIn to new matrix ready (cycles) |
|---|---|---|---|
Fixed point fi | (wl + 5)*n + 2 | 7*n2 + 27*n + 6 + 3*n*wl + 2*n*nextpow2(wl) | 7*n2 + 27*n + 6 + 3*n*wl + 2*n*nextpow2(wl) + n |
Scaled double fi | (wl + 5)*n + 2 | 7*n2 + (3*wl + 25)*n + 6 | 7*n2 + (3*wl + 25)*n + 6 + n |
double | 58*n + 2 | 7*n2 + 76*n + 6 | 7*n2 + 76*n + 6 + n |
single | 29*n + 2 | 7*n2 + 47*n + 6 | 7*n2 + 47*n + 6 + n |
This block supports HDL code generation using the Simulink® HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder) and Implement Digital Downconverter for FPGA (DSP HDL Toolbox).
This example data was generated by synthesizing the block on a Xilinx® Zynq® UltraScale™ + RFSoC ZCU111 evaluation board. The synthesis tool was Vivado® v.2020.2 (win64).
The following parameters were used for synthesis.
Block parameters:
m = 16n = 16p = 1Matrix A dimension: 16-by-16
Matrix B dimension: 16-by-1
Input data type:
sfix16_En14Target frequency: 250 MHz
The following tables show the post place-and-route resource utilization results and timing summary, respectively.
| Resource | Usage | Available | Utilization (%) |
|---|---|---|---|
| CLB LUTs | 13653 | 425280 | 3.21 |
| CLB Registers | 15739 | 850560 | 1.85 |
| DSPs | 4 | 4272 | 0.09 |
| Block RAM Tile | 0 | 1080 | 0.00 |
| URAM | 0 | 80 | 0.00 |
| Value | |
|---|---|
| Requirement | 4 ns |
| Data Path Delay | 3.468 ns |
| Slack | 0.427 ns |
| Clock Frequency | 279.88 MHz |
References
[1] "AMBA AXI and ACE Protocol Specification Version E." https://developer.arm.com/documentation/ihi0022/e/AMBA-AXI3-and-AXI4-Protocol-Specification/Single-Interface-Requirements/Basic-read-and-write-transactions/Handshake-process
Extended Capabilities
Slope-bias representation is not supported for fixed-point data types.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block has one default HDL architecture.
| General | |
|---|---|
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
Supports fixed-point data types only.
Version History
Introduced in R2020aThe Real Burst Matrix Solve Using Q-less QR Decomposition block now supports the Tikhonov Regularization parameter.
See Also
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)