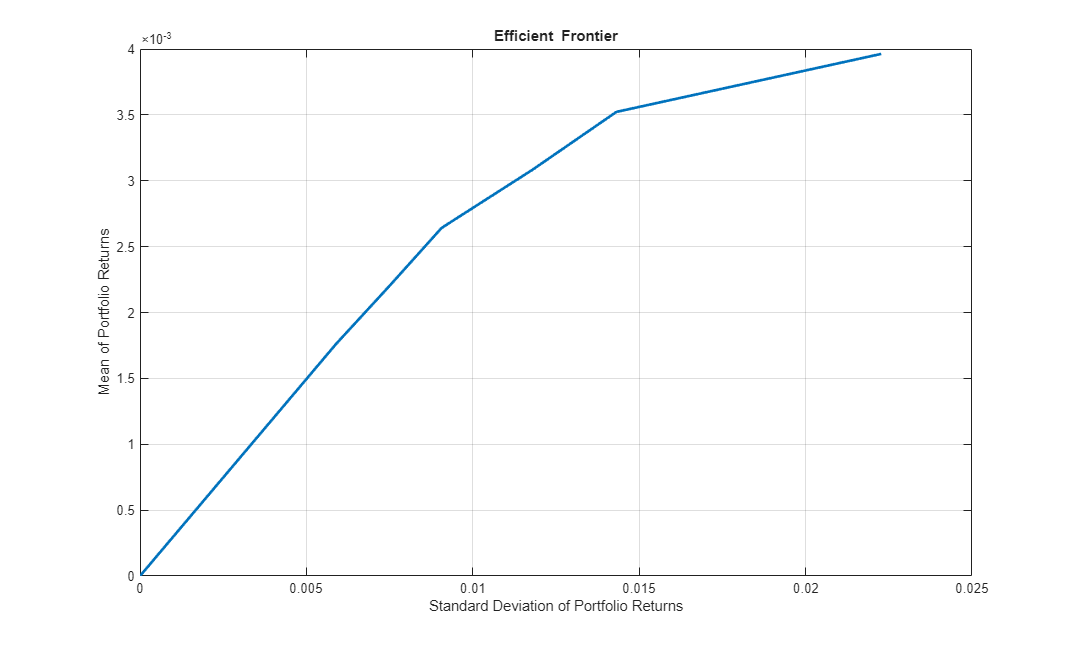
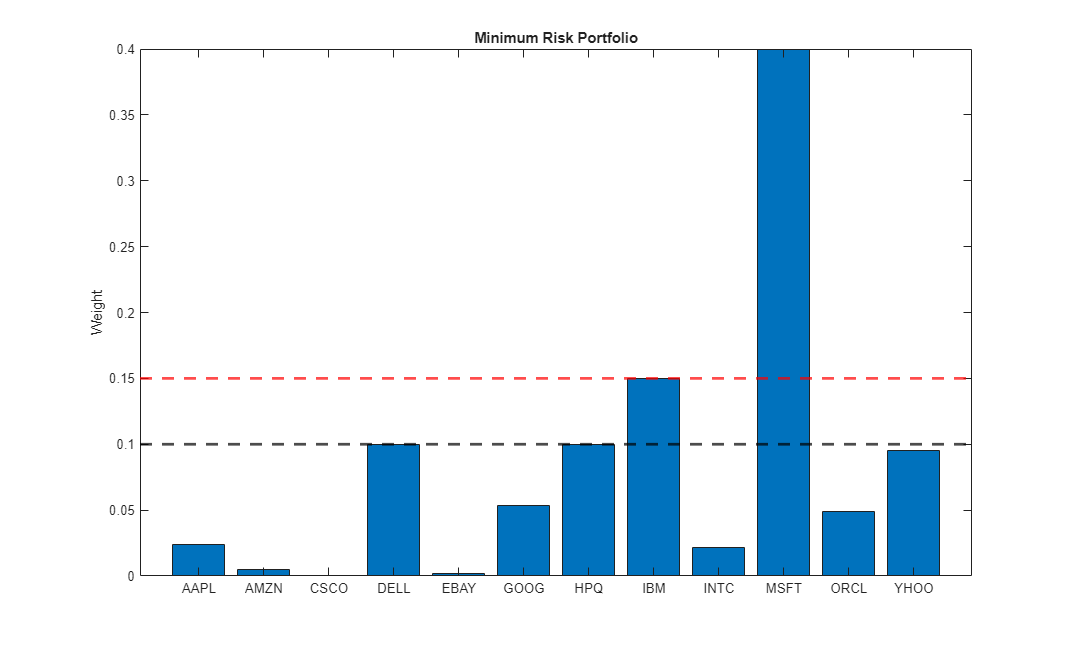
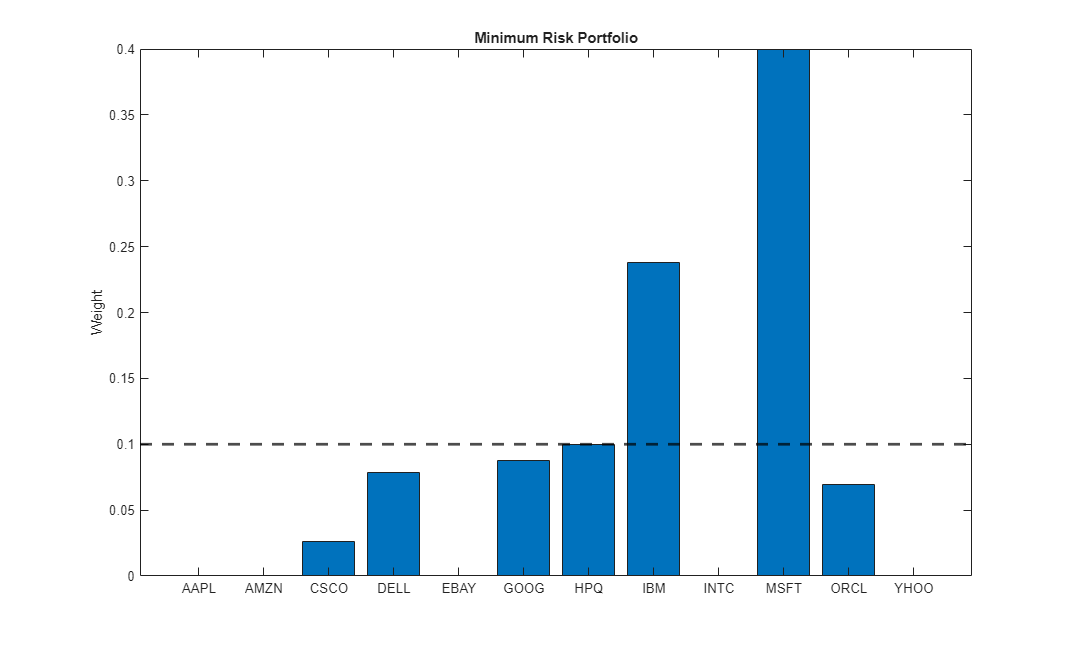
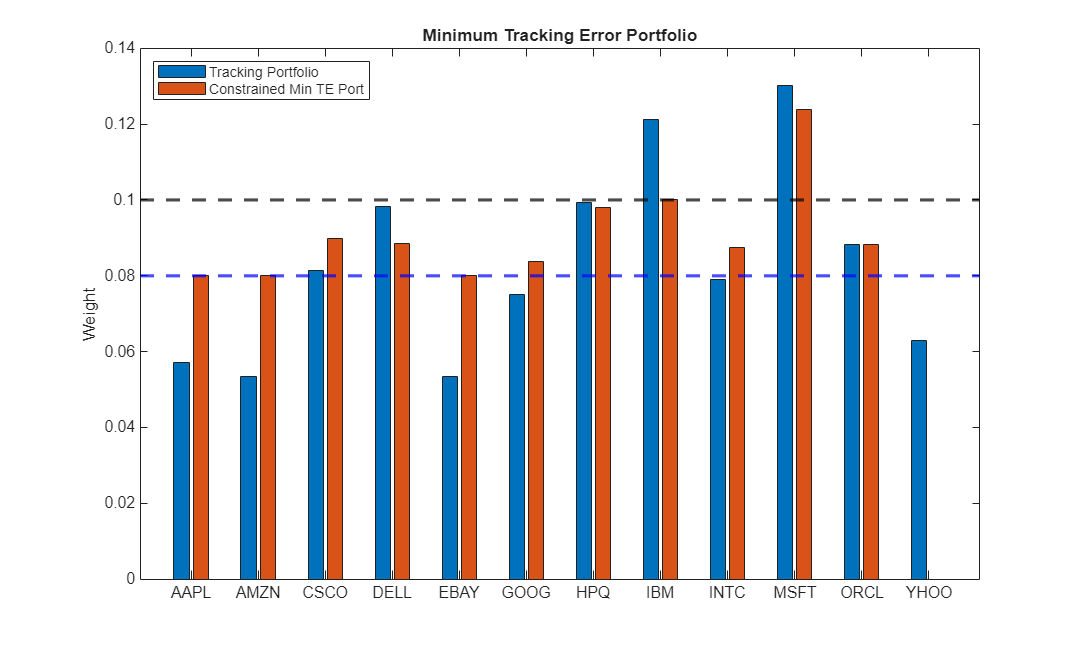
setConditionalBudget

Set up conditional budget constraints for portfolio

Since R2024b

Syntax

obj = setConditionalBudget(obj,ConditionalBudgetThreshold,ConditionalUpperBudget)

Description

obj = setConditionalBudget(obj,ConditionalBudgetThreshold,ConditionalUpperBudget) sets up conditional budget constraints for Portfolio, PortfolioCVaR, or PortfolioMAD objects. If the weight of an asset exceeds the ConditionalBudgetThreshold value, the weight of that asset is added to the aggregate sum that is bound by the ConditionalUpperBudget value. For more information, see Conditional Budget Constraints .

This constraint supports the Undertakings for Collective Investment in Transferable Securities (UCITS) Directive. The UCITS asset regulation states that any investments in excess of 5% must not exceed 40% of the total portfolio. This constraint is a conditional budget constraint. For more information, see Undertakings for Collective Investment in Transferable Securities and Adding Constraints to Satisfy UCITS Directive.

For details on the respective workflows when using these different objects, see Portfolio Object Workflow, PortfolioCVaR Object Workflow, and PortfolioMAD Object Workflow.

Examples

Add Conditional Budget Constraints

This example shows the workflow to add a conditional budget constraint for a portfolio optimization problem. The conditional budget constraint enforces a limit on the total proportion that you can invest in assets that pass a prescribed threshold.

In mathematical terms, the conditional budget constraint has the following form:

$$\sum _{\mathit{i}\in \mathit{I}}{\mathit{w}}_{\mathit{i}}\le \beta$$

where $\mathit{I}=\left\{\mathit{i}|{\mathit{w}}_{\mathit{i}}\ge {\alpha }_{\mathit{i}}\right\}$ and $\mathit{w}$ represents the asset weights.

Create Portfolio Object

To solve a portfolio problem with this constraint, start by creating a Portfolio object with default constraints. In addition to using a Portfolio object, you can also perform this workflow using a PortfolioCVaR or PortfolioMAD object.

% Load data
load CAPMuniverse.mat
tol = 1e-8;
p = Portfolio('AssetList',Assets(1:12));
p = estimateAssetMoments(p,Data(:,1:12));

Using setConditionalBudget, set a conditional budget constraint that limits the aggregate weight that can be invested in assets that exceed 10% to 50%.

% Assets with weights above 10% must not exceed 50% of the total portfolio
p = setConditionalBudget(p,0.1,0.5);

At this point, the portfolio problem is unbounded and computing any optimal portfolio results in an error. Use setBounds to add bounds to the portfolio weights.

% Weights must be between -1 and 1
p = setBounds(p,-1,1);

Compute Efficient Frontier

The most common workflow is to estimate a set of portfolios on the efficient frontier. The efficient frontier is the curve that shows the tradeoff between the return and risk achieved by Pareto-optimal portfolios. For a given return level, the portfolio on the efficient frontier is the one that minimizes the risk while maintaining the desired return. Conversely, for a given risk level, the portfolio on the efficient frontier is the one that maximizes return while maintaining the desired risk level.

% Compute efficient frontier
w = estimateFrontier(p)

w = 12×10

    0.0000    0.0368    0.0737    0.1105    0.1473    0.1979    0.2408    0.2686    0.5000    0.5000
    0.0000    0.0008    0.0016    0.0023    0.0031    0.0082    0.0108    0.0762    0.0317    0.1000
    0.0000   -0.0222   -0.0444   -0.0665   -0.0887   -0.1084   -0.1294   -0.2283   -0.2164   -1.0000
   -0.0000   -0.0218   -0.0436   -0.0654   -0.0871   -0.1144   -0.1386   -0.4499   -0.4361   -1.0000
    0.0000   -0.0087   -0.0175   -0.0262   -0.0350   -0.0448   -0.0539   -0.0260   -0.0300    0.1000
   -0.0000    0.0398    0.0796    0.1194    0.1592    0.2122    0.2578    0.2314    0.1000    0.1000
    0.0000    0.0366    0.0732    0.1098    0.1464    0.1000    0.1000    0.1000    0.1000    0.1000
   -0.0000   -0.0282   -0.0565   -0.0847   -0.1129   -0.1424   -0.1712   -0.1291   -0.2717    0.1000
    0.0000    0.0060    0.0120    0.0180    0.0240    0.0506    0.0658    0.1000    0.1000    0.1000
   -0.0000    0.0111    0.0222    0.0333    0.0444    0.0746    0.0941    0.1000    0.1000    0.1000
      ⋮

plotFrontier(p,w)

Check that none of the assets that exceed 10% go above 50%.

% Keep weights above 10% threshold
auxW = w;
auxW(w <= 0.1 + tol) = 0;
conditionalBudget = sum(auxW)

conditionalBudget = 1×10

         0         0         0    0.3397    0.4529    0.4101    0.4986    0.5000    0.5000    0.5000

Set Different Conditional Budget Thresholds for Different Assets

This example shows how to set a different conditional budget threshold for one of the assets in the portfolio. setConditionalBudget supports a vector input for the CondtionalBudgetThreshold argument, where each entry represents the conditional threshold for each asset. In this example, assume that the conditional budget threshold for all assets is 10% except for IBM. The conditional budget threshold for IBM is 15%.

To solve a portfolio problem with this constraint, start by creating a PortfolioCVaR object with default constraints. In addition to using a PortfolioCVaR object, you can also perform this workflow using a Portfolio or PortfolioMAD object.

% Load data
load CAPMuniverse.mat
tol = 1e-8;
startRow = find(~isnan(Data(:,6)),1);
p = PortfolioCVaR(AssetList=Assets(1:12), ...
    AssetScenarios=Data(startRow:end,1:12),ProbabilityLevel=0.95);
p = setDefaultConstraints(p);

The objective of the minimum variance problem is to find the weights (properties of the total investment) allocated to each asset in the portfolio that result in the lowest possible risk.

threshold = 0.1*ones(p.NumAssets,1);
threshold(strcmpi('IBM',p.AssetList)) = 0.15;
p = setConditionalBudget(p,threshold,0.4);

% Solve the minimum risk problem
wMin = estimateFrontierLimits(p,'min');
figure
bar(Assets(1:12),wMin);
hold on
yline(0.1,'k--',LineWidth=2)
yline(0.15,'r--',LineWidth=2)
title('Minimum Risk Portfolio')
ylabel('Weight')

All assets except IBM and MSFT do not exceed the 10% threshold, IBM does not exceed the 15% threshold, and the sum of all the assets above their conditional threshold (in this case only MSFT) is less than 40%.

Excluding One Asset from Conditional Budget Constraint

This example shows how to exclude individual assets from the conditional budget constraint.

Create a PortfolioMAD object. In addition to using a PortfolioMAD object, you can also perform this workflow using a Portfolio or PortfolioCVaR object.

% Load data
load CAPMuniverse.mat
tol = 1e-8;
% Create a PortfolioMAD object with default constraints
startRow = find(~isnan(Data(:,6)),1);
q = PortfolioMAD(AssetList=Assets(1:12), ...
    AssetScenarios=Data(startRow:end,1:12));

% Nonnegative and fully invested portfolios
q = setDefaultConstraints(q);

To exclude any asset from the conditional budget constraint, set the ConditionalBudgetThreshold of that asset to Inf. In this example, you can exclude IBM from the conditional budget constraint.

% Conditional budget
threshold = 0.1*ones(q.NumAssets,1);
threshold(strcmpi('IBM',q.AssetList)) = Inf;
q2 = setConditionalBudget(q,threshold,0.4);

% Solve minimum risk problem
wMin2 = estimateFrontierLimits(q2,'min');
figure
bar(Assets(1:12),wMin2);
hold on
yline(0.1,'k--',LineWidth=2)
title('Minimum Risk Portfolio')
ylabel('Weight')

Working with Conditional Budget and Other Constraints

This example shows how to combine the conditional budget constraint with other types of constraints. Specifically, the example shows how to add semicontinuous bounds on the assets together with a conditional budget constraint, while ensuring that the portfolio is fully invested.

Create a mean-variance Portfolio object with default constraints.

% Load data
load CAPMuniverse.mat
tol = 1e-8;
p = Portfolio('AssetList',Assets(1:12));
p = estimateAssetMoments(p,Data(:,1:12));

Use setBounds to ensure that any asset that is chosen in the portfolio has a weight of at least 8% and at most 15%. Then, use setBudget to set the fully invested constraint.

% Assets must be either 0 or between 8% and 15%
p = setBounds(p,0.08,0.15,BoundType="conditional");

% Assets must sum to 1
p = setBudget(p,1,1);

% Conditional budget
p = setConditionalBudget(p,0.1,0.2);

To find the minimum tracking error portfolio that satisfies all the previously specified constraints, use the risk parity portfolio as the benchmark portfolio.

% Solve minimum tracking error portfolio
trackingPort = riskBudgetingPortfolio(p.AssetCovar);
TE = @(w) (w-trackingPort)'*p.AssetCovar*(w-trackingPort);
wTE = estimateCustomObjectivePortfolio(p,TE);
figure
bar(Assets(1:12),[trackingPort wTE]);
hold on
yline(0.1,'k--',LineWidth=2)
yline(0.08,'b--',LineWidth=2)
title('Minimum Tracking Error Portfolio')
ylabel('Weight')
legend('Tracking Portfolio','Constrained Min TE Port', ...
    Location='northwest')

All assets for the constrained portfolio are either zero or have at least a 0.08 weight, which means that the semicontinuous bound is satisfied. Furthermore, the sum of the assets above the 0.1 threshold is less than 0.2, and this result is also consistent with the conditional budget.

Input Arguments

obj — Object for portfolio

Portfolio object | PortfolioCVaR object | PortfolioMAD object

Object for portfolio, specified using the Portfolio, PortfolioCVaR, or PortfolioMAD object. For more information on creating a portfolio object, see:

• Portfolio

• PortfolioCVaR

• PortfolioMAD

Data Types: object

ConditionalBudgetThreshold — Weights threshold above which asset is accounted for in conditional budget

scalar numeric | numeric vector

Weights threshold above which the asset is accounted for in the conditional budget, specified as a scalar or a NumAssets-by-1 vector for a Portfolio, PortfolioCVaR, or PortfolioMAD input object (obj). The ConditionalBudgetThreshold value can be a positive or negative value. However, this value cannot be NaN or -Inf.

The ConditionalBudgetThreshold value indicates whether an asset should be accounted for in the aggregate sum or not. If the weight of an asset exceeds the ConditionalBudgetThreshold value, the weight of that asset is added to the aggregate sum that is bound by the ConditionalBudgetThreshold value.

Note

All assets for the ConditionalBudgetThreshold value are larger than or equal to the ConditionalUpperBudget value, then the conditional budget constraint is always feasible, so Financial Toolbox™ issues the following message: Warning: Redundant conditional budget constraint.

Data Types: double

ConditionalUpperBudget — Maximum aggregate weight of portfolio that can be invested in assets that exceed ConditionalBudgetThreshold

scalar numeric

Maximum aggregate weight of the portfolio that can be invested in assets that exceed the ConditionalBudgetThreshold value, specified as a scalar for a Portfolio, PortfolioCVaR, or PortfolioMAD input object (obj). The ConditionalUpperBudget value can be positive or negative. However, this value cannot be NaN or -Inf.

Data Types: double

Output Arguments

obj — Updated portfolio object

Updated Portfolio object | Updated PortfolioCVaR object | Updated PortfolioMAD object

Updated portfolio object, returned as a Portfolio, PortfolioCVaR, or PortfolioMAD object. For more information on creating a portfolio object, see:

• Portfolio

• PortfolioCVaR

• PortfolioMAD

More About

Undertakings for Collective Investment in Transferable Securities

Undertakings for Collective Investment in Transferable Securities (UCITS) is a regulatory framework of the European Union that creates a harmonized regime throughout Europe for the management and sale of mutual funds.

UCITS funds are subject to strict rules regarding investment diversification and risk management to protect investors against concentration risk. One of the core principles of UCITS is investment diversification. This principle reduces the risk associated with concentrating investments in a single issuer or asset class. By spreading investments across various assets, UCITS funds aim to mitigate individual asset volatility and reduce the overall risk profile of the portfolio.

The diversification rules for a UCITS fund state that a fund cannot hold more than 10% of its assets in securities or money market instruments issued by a single body. Additionally, any investments in excess of 5% must not exceed 40% of the total portfolio. This rule is known as the 5/10/40 rule.

Tips

You can also use dot notation to set up the conditional budget constraints.

obj = obj.setConditionalBudget(ConditionalBudgetThreshold,ConditionalUpperBudget);

Version History

Introduced in R2024b