Stochastic Process Characteristics
What Is a Stochastic Process?
A time series yt is a collection of observations on a variable indexed sequentially over several time points t = 1, 2,...,T. Time series observations y1, y2,...,yT are inherently dependent. From a statistical modeling perspective, this means it is inappropriate to treat a time series as a random sample of independent observations.
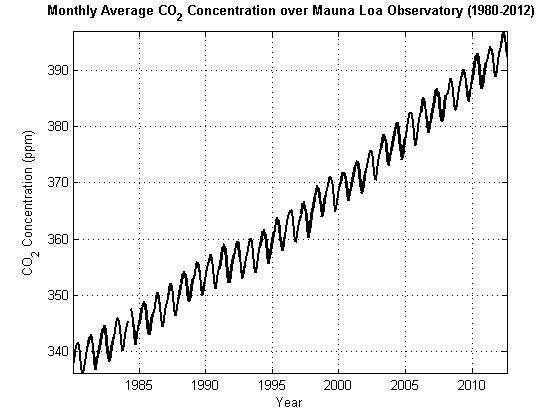
The goal of statistical modeling is finding a compact representation of the data-generating process for your data. The statistical building block of econometric time series modeling is the stochastic process. Heuristically, a stochastic process is a joint probability distribution for a collection of random variables. By modeling the observed time series yt as a realization from a stochastic process , it is possible to accommodate the high-dimensional and dependent nature of the data. The set of observation times T can be discrete or continuous. Figure 1-1, Monthly Average CO2 displays the monthly average CO2 concentration (ppm) recorded by the Mauna Loa Observatory in Hawaii from 1980 to 2012 [3].
Figure 1-1, Monthly Average CO2
Stationary Processes
Stochastic processes are weakly stationary or covariance stationary (or simply, stationary) if their first two moments are finite and constant over time. Specifically, if yt is a stationary stochastic process, then for all t:
E(yt) = μ < ∞.
V(yt) = < ∞.
Cov(yt, yt–h) = γh for all lags
Does a plot of your stochastic process seem to increase or decrease without bound? The answer to this question indicates whether the stochastic process is stationary. “Yes” indicates that the stochastic process might be nonstationary. In Figure 1-1, Monthly Average CO2, the concentration of CO2 is increasing without bound which indicates a nonstationary stochastic process.
Linear Time Series Model
Wold’s theorem [2] states that you can write all weakly stationary stochastic processes in the general linear form
Here, denotes a sequence of uncorrelated (but not necessarily independent) random variables from a well-defined probability distribution with mean zero. It is often called the innovation process because it captures all new information in the system at time t.
Unit Root Process
A linear time series model is a unit root process if the solution set to its characteristic equation contains a root that is on the unit circle (i.e., has an absolute value of one). Subsequently, the expected value, variance, or covariance of the elements of the stochastic process grows with time, and therefore is nonstationary. If your series has a unit root, then differencing it might make it stationary.
For example, consider the linear time series model where is a white noise sequence of innovations with variance σ2 (this is called the random walk). The characteristic equation of this model is which has a root of one. If the initial observation y0 is fixed, then you can write the model as Its expected value is y0, which is independent of time. However, the variance of the series is tσ2, which grows with time making the series unstable. Take the first difference to transform the series and the model becomes . The characteristic equation for this series is , so it does not have a unit root. Note that
which is independent of time,
which is independent of time, and
which is independent of time for all integers 0 < s < t.
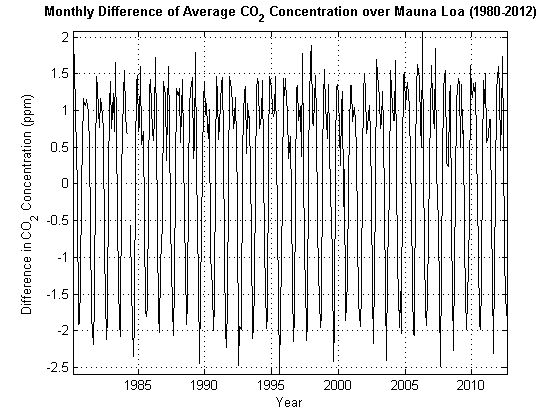
Figure 1-1, Monthly Average CO2 appears nonstationary. What happens if you plot the first difference dt = yt – yt–1 of this series? Figure 1-2, Monthly Difference in CO2 displays the dt. Ignoring the fluctuations, the stochastic process does not seem to increase or decrease in general. You can conclude that dt is stationary, and that yt is unit root nonstationary. For details, see Differencing.
Figure 1-2, Monthly Difference in CO2
Lag Operator Notation
The lag operator L operates on a time series yt such that .
An mth-degree lag polynomial of coefficients b1, b2,...,bm is defined as
In lag operator notation, you can write the general linear model using an infinite-degree polynomial
You cannot estimate a model that has an infinite-degree polynomial of coefficients with a finite amount of data. However, if is a rational polynomial (or approximately rational), you can write it (at least approximately) as the quotient of two finite-degree polynomials.
Define the q-degree polynomial and the p-degree polynomial . If is rational, then
Thus, by Wold’s theorem, you can model (or closely approximate) every stationary stochastic process as
which has p + q coefficients (a finite number).
Characteristic Equation
A degree p characteristic polynomial of the linear time series model is
It is another way to assess that a series is a stationary process. For example, the characteristic equation of is
The roots of the homogeneous characteristic equation (called the characteristic roots) determine whether the linear time series is stationary. If every root in lies inside the unit circle, then the process is stationary. Roots lie within the unit circle if they have an absolute value less than one. This is a unit root process if one or more roots lie inside the unit circle (i.e., have absolute value of one). Continuing the example, the characteristic roots of are Since the absolute values of these roots are less than one, the linear time series model is stationary.
References
[1] Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.
[2] Wold, H. A Study in the Analysis of Stationary Time Series. Uppsala, Sweden: Almqvist & Wiksell, 1938.
[3] Tans, P., and R. Keeling. (2012, August). “Trends
in Atmospheric Carbon Dioxide.” NOAA Research.
Retrieved October 5, 2012 from https://gml.noaa.gov/ccgg/trends/mlo.html.