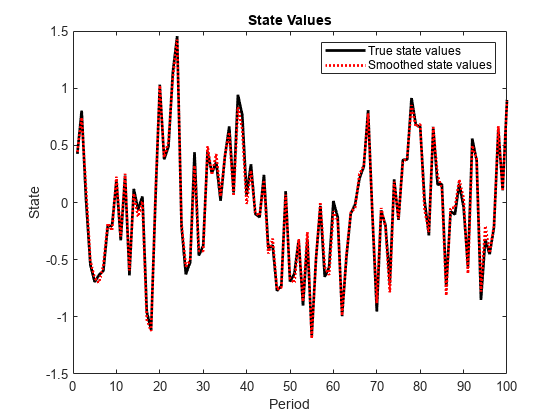
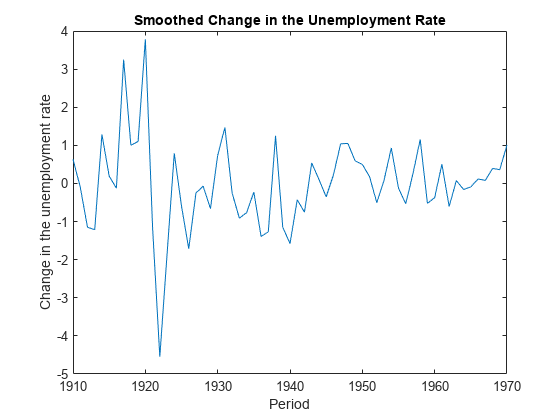
smooth

Class: ssm

Backward recursion of state-space models

Syntax

X = smooth(Mdl,Y)

X = smooth(Mdl,Y,Name,Value)

[X,logL,Output] = smooth(___)

Description

X = smooth(Mdl,Y) returns smoothed states (X) by performing backward recursion of the fully-specified state-space model Mdl. That is, smooth applies the standard Kalman filter using Mdl and the observed responses Y.

X = smooth(Mdl,Y,Name,Value) uses additional options specified by one or more Name,Value pair arguments.

If Mdl is not fully specified, then you must set the unknown parameters to known scalars using the Params Name,Value pair argument.

[X,logL,Output] = smooth(___) uses any of the input arguments in the previous syntaxes to additionally return the loglikelihood value (logL) and an output structure array (Output) containing:

• Smoothed states and their estimated covariance matrix

• Smoothed state disturbances and their estimated covariance matrix

• Smoothed observation innovations and their estimated covariance matrix

• The loglikelihood value

• The adjusted Kalman gain

• And a vector indicating which data the software used to filter

Input Arguments

Mdl — Standard state-space model

ssm model object

Standard state-space model, specified as an ssm model object returned by ssm or estimate.

If Mdl is not fully specified (that is, Mdl contains unknown parameters), then specify values for the unknown parameters using the 'Params' name-value pair argument. Otherwise, the software issues an error. estimate returns fully-specified state-space models.

Mdl does not store observed responses or predictor data. Supply the data wherever necessary using the appropriate input or name-value pair arguments.

Y — Observed response data

numeric matrix | cell vector of numeric vectors

Observed response data to which Mdl is fit, specified as a numeric matrix or a cell vector of numeric vectors.

• If Mdl is time invariant with respect to the observation equation, then Y is a T-by-n matrix, where each row corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and m is the number of observations per period. The last row of Y contains the latest observations.

• If Mdl is time varying with respect to the observation equation, then Y is a T-by-1 cell vector. Each element of the cell vector corresponds to a period and contains an n_t-dimensional vector of observations for that period. The corresponding dimensions of the coefficient matrices in Mdl.C{t} and Mdl.D{t} must be consistent with the matrix in Y{t} for all periods. The last cell of Y contains the latest observations.

NaN elements indicate missing observations. For details on how the Kalman filter accommodates missing observations, see Algorithms.

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: 'Beta',beta,'Predictors',Z specifies to deflate the observations by the regression component composed of the predictor data Z and the coefficient matrix beta.

'Beta' — Regression coefficients

[] (default) | numeric matrix

Regression coefficients corresponding to predictor variables, specified as the comma-separated pair consisting of 'Beta' and a d-by-n numeric matrix. d is the number of predictor variables (see Predictors) and n is the number of observed response series (see Y).

If Mdl is an estimated state-space model, then specify the estimated regression coefficients stored in estParams.

'Params' — Values for unknown parameters

numeric vector

Values for unknown parameters in the state-space model, specified as the column-separated pair consisting of 'Params' and a numeric vector.

The elements of Params correspond to the unknown parameters in the state-space model matrices A, B, C, and D, and, optionally, the initial state mean Mean0 and covariance matrix Cov0.

• If you created Mdl explicitly (that is, by specifying the matrices without a parameter-to-matrix mapping function), then the software maps the elements of Params to NaNs in the state-space model matrices and initial state values. The software searches for NaNs column-wise following the order A, B, C, D, Mean0, and Cov0.

• If you created Mdl implicitly (that is, by specifying the matrices with a parameter-to-matrix mapping function), then you must set initial parameter values for the state-space model matrices, initial state values, and state types within the parameter-to-matrix mapping function.

If Mdl contains unknown parameters, then you must specify their values. Otherwise, the software ignores the value of Params.

Data Types: double

'Predictors' — Predictor variables in state-space model observation equation

[] (default) | numeric matrix

Predictor variables in the state-space model observation equation, specified as the comma-separated pair consisting of 'Predictors' and a T-by-d numeric matrix. T is the number of periods and d is the number of predictor variables. Row t corresponds to the observed predictors at period t (Z_t). The expanded observation equation is

$$y_t-Z_t\beta =C{x}_t+D{u}_t.$$

That is, the software deflates the observations using the regression component. β is the time-invariant vector of regression coefficients that the software estimates with all other parameters.

If there are n observations per period, then the software regresses all predictor series onto each observation.

If you specify Predictors, then Mdl must be time invariant. Otherwise, the software returns an error.

By default, the software excludes a regression component from the state-space model.

Data Types: double

'SquareRoot' — Square root filter method flag

false (default) | true

Square root filter method flag, specified as the comma-separated pair consisting of 'SquareRoot' and true or false. If true, then estimate applies the square root filter method when implementing the Kalman filter.

If you suspect that the eigenvalues of the filtered state or forecasted observation covariance matrices are close to zero, then specify 'SquareRoot',true. The square root filter is robust to numerical issues arising from finite the precision of calculations, but requires more computational resources.

Example: 'SquareRoot',true

Data Types: logical

'Tolerance' — Forecast uncertainty threshold

0 (default) | nonnegative scalar

Forecast uncertainty threshold, specified as the comma-separated pair consisting of 'Tolerance' and a nonnegative scalar.

If the forecast uncertainty for a particular observation is less than Tolerance during numerical estimation, then the software removes the uncertainty corresponding to the observation from the forecast covariance matrix before its inversion.

It is best practice to set Tolerance to a small number, for example, le-15, to overcome numerical obstacles during estimation.

Example: 'Tolerance',le-15

Data Types: double

'Univariate' — Univariate treatment of multivariate series flag

false (default) | true

Univariate treatment of a multivariate series flag, specified as the comma-separated pair consisting of 'Univariate' and true or false. Univariate treatment of a multivariate series is also known as sequential filtering.

The univariate treatment can accelerate and improve numerical stability of the Kalman filter. However, all observation innovations must be uncorrelated. That is, D_tD_t' must be diagonal, where D_t, t = 1,...,T, is one of the following:

• The matrix D{t} in a time-varying state-space model

• The matrix D in a time-invariant state-space model

Example: 'Univariate',true

Data Types: logical

Output Arguments

X — Smoothed states

matrix | cell vector of vectors

Smoothed states, returned as a matrix or a cell vector of matrices.

If Mdl is time invariant, then the number of rows of X is the sample size, and the number of columns of X is the number of states. The last row of X contains the latest smoothed states.

If Mdl is time varying, then X is a cell vector with length equal to the sample size. Cell t of X contains a vector of smoothed states with length equal to the number of states in period t. The last cell of X contains the latest smoothed states.

Data Types: cell | double

logL — Loglikelihood function value

scalar

Loglikelihood function value, returned as a scalar.

Missing observations do not contribute to the loglikelihood.

Output — Smoothing results by period

structure array

Smoothing results by period, returned as a structure array.

Output is a T-by-1 structure, where element t corresponds to the smoothing recursion at time t.

• If Univariate is false (it is by default), then the following table describes the fields of Output.

  Field	Description	Estimate
  LogLikelihood	Scalar loglikelihood objective function value	N/A
  SmoothedStates	mt-by-1 vector of smoothed states	$$E\left(x_t|y_1,\mathrm{...},y_T\right)$$
  SmoothedStatesCov	mt-by-mt variance-covariance matrix of the smoothed states	$$Var\left(x_t|y_1,\mathrm{...},y_T\right)$$
  SmoothedStateDisturb	kt-by-1 vector of smoothed state disturbances	$$E\left(u_t|y_1,\mathrm{...},y_T\right)$$
  SmoothedStateDisturbCov	kt-by-kt variance-covariance matrix of the smoothed, state disturbances	$$Var\left(u_t|y_1,\mathrm{...},y_T\right)$$
  SmoothedObsInnov	ht-by-1 vector of smoothed observation innovations	$$E\left({\epsilon }_t|y_1,\mathrm{...},y_T\right)$$
  SmoothedObsInnovCov	ht-by-ht variance-covariance matrix of the smoothed, observation innovations	$$Var\left({\epsilon }_t|y_1,\mathrm{...},y_T\right)$$
  KalmanGain	mt-by-nt adjusted Kalman gain matrix	N/A
  DataUsed	ht-by-1 logical vector indicating whether the software filters using a particular observation. For example, if observation i at time t is a NaN, then element i in DataUsed at time t is 0.	N/A

• If Univarite is true, then the fields of Output are the same as in the previous table, but the values in KalmanGain might vary.

Examples

Smooth States of Time-Invariant State-Space Model

Suppose that a latent process is an AR(1). Subsequently, the state equation is

where is Gaussian with mean 0 and standard deviation 0.5.

Generate a random series of 100 observations from , assuming that the series starts at 1.5.

T = 100;
ARMdl = arima('AR',0.5,'Constant',0,'Variance',0.5^2);
x0 = 1.5;
rng(1); % For reproducibility
x = simulate(ARMdl,T,'Y0',x0);

Suppose further that the latent process is subject to additive measurement error. Subsequently, the observation equation is

where is Gaussian with mean 0 and standard deviation 0.05. Together, the latent process and observation equations compose a state-space model.

Use the random latent state process (x) and the observation equation to generate observations.

y = x + 0.05*randn(T,1);

Specify the four coefficient matrices.

A = 0.5;
B = 0.5;
C = 1;
D = 0.05;

Specify the state-space model using the coefficient matrices.

Mdl = ssm(A,B,C,D)

Mdl = 
State-space model type: ssm

State vector length: 1
Observation vector length: 1
State disturbance vector length: 1
Observation innovation vector length: 1
Sample size supported by model: Unlimited

State variables: x1, x2,...
State disturbances: u1, u2,...
Observation series: y1, y2,...
Observation innovations: e1, e2,...

State equation:
x1(t) = (0.50)x1(t-1) + (0.50)u1(t)

Observation equation:
y1(t) = x1(t) + (0.05)e1(t)

Initial state distribution:

Initial state means
 x1 
  0 

Initial state covariance matrix
     x1   
 x1  0.33 

State types
     x1     
 Stationary 

Mdl is an ssm model. Verify that the model is correctly specified using the display in the Command Window. The software infers that the state process is stationary. Subsequently, the software sets the initial state mean and covariance to the mean and variance of the stationary distribution of an AR(1) model.

Smooth the states for periods 1 through 100. Plot the true state values and the smoothed states.

SmoothedX = smooth(Mdl,y);

figure
plot(1:T,x,'-k',1:T,SmoothedX,':r','LineWidth',2)
title({'State Values'})
xlabel('Period')
ylabel('State')
legend({'True state values','Smoothed state values'})

Smooth States of State-Space Model Containing Regression Component

Suppose that the linear relationship between the change in the unemployment rate and the nominal gross national product (nGNP) growth rate is of interest. Suppose further that the first difference of the unemployment rate is an ARMA(1,1) series. Symbolically, and in state-space form, the model is

where:

• is the change in the unemployment rate at time t.

• is a dummy state for the MA(1) effect.

• is the observed unemployment rate being deflated by the growth rate of nGNP ().

• is the Gaussian series of state disturbances having mean 0 and standard deviation 1.

• is the Gaussian series of observation innovations having mean 0 and standard deviation .

Load the Nelson-Plosser data set, which contains the unemployment rate and nGNP series, among other things.

load Data_NelsonPlosser

Preprocess the data by taking the natural logarithm of the nGNP series, and the first difference of each series. Also, remove the starting NaN values from each series.

isNaN = any(ismissing(DataTable),2);       % Flag periods containing NaNs
gnpn = DataTable.GNPN(~isNaN);
u = DataTable.UR(~isNaN);
T = size(gnpn,1);                          % Sample size
Z = [ones(T-1,1) diff(log(gnpn))];
y = diff(u);

Though this example removes missing values, the software can accommodate series containing missing values in the Kalman filter framework.

Specify the coefficient matrices.

A = [NaN NaN; 0 0];
B = [1; 1];
C = [1 0];
D = NaN;

Specify the state-space model using ssm.

Mdl = ssm(A,B,C,D);

Estimate the model parameters. Specify the regression component and its initial value for optimization using the 'Predictors' and 'Beta0' name-value pair arguments, respectively. Restrict the estimate of to all positive, real numbers.

params0 = [0.3 0.2 0.2]; % Chosen arbitrarily
[EstMdl,estParams] = estimate(Mdl,y,params0,'Predictors',Z,...
    'Beta0',[0.1 0.2],'lb',[-Inf,-Inf,0,-Inf,-Inf]);

Method: Maximum likelihood (fmincon)
Sample size: 61
Logarithmic  likelihood:     -99.7245
Akaike   info criterion:      209.449
Bayesian info criterion:      220.003
           |      Coeff       Std Err    t Stat     Prob  
----------------------------------------------------------
 c(1)      |  -0.34098       0.29608    -1.15164  0.24948 
 c(2)      |   1.05003       0.41377     2.53771  0.01116 
 c(3)      |   0.48592       0.36790     1.32079  0.18657 
 y <- z(1) |   1.36121       0.22338     6.09358   0      
 y <- z(2) | -24.46711       1.60018   -15.29024   0      
           |                                              
           |    Final State   Std Dev     t Stat    Prob  
 x(1)      |   1.01264       0.44690     2.26592  0.02346 
 x(2)      |   0.77718       0.58917     1.31912  0.18713 

EstMdl is an ssm model, and you can access its properties using dot notation.

Smooth the states. EstMdl does not store the data or the regression coefficients, so you must pass in them in using the name-value pair arguments 'Predictors' and 'Beta', respectively. Plot the smoothed states. Recall that the first state is the change in the unemployment rate, and the second state helps build the first.

SmoothedX = smooth(EstMdl,y,'Predictors',Z,'Beta',estParams(end-1:end));

figure
plot(dates(end-(T-1)+1:end),SmoothedX(:,1));
xlabel('Period')
ylabel('Change in the unemployment rate')
title('Smoothed Change in the Unemployment Rate')

Tips

• Mdl does not store the response data, predictor data, and the regression coefficients. Supply the data wherever necessary using the appropriate input or name-value pair arguments.

• To accelerate estimation for low-dimensional, time-invariant models, set 'Univariate',true. Using this specification, the software sequentially updates rather then updating all at once during the filtering process.

Algorithms

• The Kalman filter accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.

• For explicitly defined state-space models, smooth applies all predictors to each response series. However, each response series has its own set of regression coefficients.

References

[1] Durbin J., and S. J. Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.