Moving Average
Moving average
Libraries:
DSP System Toolbox /
Statistics
Description
The Moving Average block computes the moving average of the input signal along each channel independently over time. The block uses the sliding window method or the exponential weighting method to compute the moving average. In the sliding window method, a window of specified length moves over the data sample by sample, and the block computes the average over the data in the window. In the exponential weighting method, the block multiplies the data samples with a set of weighting factors and then sums the weighted data to compute the average. For more details on these methods, see Algorithms.
Examples
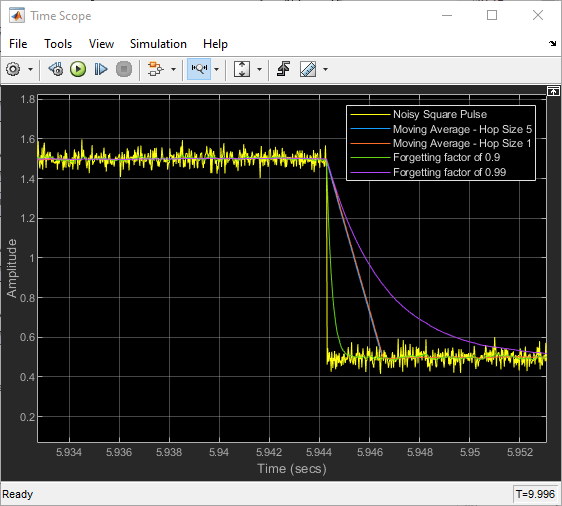
Compute Moving Average of Noisy Step Signal
Compare the sliding window averaging method and the exponentially weighted averaging method in Simulink® using the Moving Average block.
Ports
Input
The block computes the moving average of the data specified at this input port. Specify real- or complex-valued multichannel inputs of the size m-by-n, where m ≥ 1 and n ≥ 1.
When the Allow arbitrary frame length for fixed-size input signals parameter appears and is not selected, and you input a fixed-size signal, the frame length must be a multiple of the hop size (window length − overlap length). In all other cases, the input frame length can be arbitrary.
The block accepts variable-size inputs (frame length changes during simulation). When you input a variable-size signal, the frame length of the signal can be arbitrary.
This port is unnamed until you set Method to
Exponential weighting and select the Specify forgetting
factor from input port parameter.
Data Types: single | double
Complex Number Support: Yes
Specify the forgetting factor as a non-negative real scalar in the range [0,1]. The forgetting factor determines how much weight past data is given. A forgetting factor of 0.9 gives more weight to the older data than does a forgetting factor of 0.1. A forgetting factor of 1.0 indicates infinite memory and all previous samples are given an equal weight. A forgetting factor of 0 indicates no memory and the past samples have no weight on the current computation.
Dependencies
This port appears when you set Method to Exponential
weighting and select the Specify forgetting factor from input
port parameter.
Data Types: single | double
Output
Moving average, returned as a vector or a matrix. The block computes the moving average based on the Method parameter settings using either the sliding window method or the exponential weighting method. For more details, see Algorithms.
This table provides more details on the dimensions of the output signal.
| Input Signal | Input Dimensions | Output Dimensions When Allow arbitrary frame length for fixed-size input signals Appears | Output Dimensions When Allow arbitrary frame length for fixed-size input signals Does Not Appear |
|---|---|---|---|
| Fixed-size signal | m-by-n, where m is a multiple of the hop size (window length − overlap length) | (m/hop size)-by-n | m-by-n |
| Fixed-size signal | m-by-n, where m is not a multiple of the hop size (window length − overlap length) |
If you do not select Allow arbitrary frame length for fixed-size input signals, the block errors. | m-by-n |
| Variable-size signal | m-by-n | ceil(m/hop
size)-by-n | m-by-n |
When the output has an upper bound size of
ceil(m/hop size)-by-n, during
simulation, the size of the first dimension varies within this bound and the size of the
second dimension remains constant. For an example that shows this behavior, see Compute Moving Average of Noisy Step Signal.
Data Types: single | double
Complex Number Support: Yes
Parameters
If a parameter is listed as tunable, then you can change its value during simulation.
Sliding window— A window of length Window length moves over the input data along each channel. For every sample the window moves over, the block computes the average over the data in the window.Exponential weighting— The block multiplies the samples by a set of weighting factors. The magnitude of the weighting factors decreases exponentially as the age of the data increases, but the magnitude never reaches zero. To compute the average, the algorithm sums the weighted data.
When you select this check box, the length of the sliding window is equal to the value you specify in Window length. When you clear this check box, the length of the sliding window is infinite. In this mode, the block computes the average of the current sample and all previous samples in the channel.
Dependencies
To enable this parameter, set Method to Sliding
window.
Specifies the length of the sliding window in samples.
Dependencies
To enable this parameter, set Method to Sliding
window and select the Specify window length check
box.
Specify the overlap length between sliding windows as a nonnegative integer. The value of overlap length varies in the range [0, Window length − 1].
Dependencies
To enable this parameter, set Method to Sliding
window and select the Specify window length check
box.
Specify whether fixed-size input signals (whose size does not change during simulation) can have an arbitrary frame length, where the frame length does not have to be a multiple of the hop size. Hop size is defined as Window length − Overlap length. The block uses this parameter setting only for fixed-size input signals and ignores this parameter if the input has a variable-size.
When the input signal is a variable-size signal, the signal can have arbitrary frame length, that is, the frame length does not have to be a multiple of the hop size.
For fixed-size input signals, if you:
Select the Allow arbitrary frame length for fixed-size input signals parameter, the frame length of the signal does not have to be a multiple of the hop size. If the input is not a multiple of the hop size, then the output is generally a variable-size signal. Therefore, to support arbitrary input size, the block must also support variable-size operations, which you can enable by selecting the Allow arbitrary frame length for fixed-size input signals parameter.
Clear the Allow arbitrary frame length for fixed-size input signals parameter, the input frame length must be a multiple of the hop size.
Dependencies
To enable this parameter, set Method to Sliding
window and select the Specify window length check
box.
When you select this check box, the forgetting factor is input through the lambda port. When you clear this check box, the forgetting factor is specified on the block dialog through the Forgetting factor parameter.
Dependencies
To enable this parameter, set Method to Exponential
weighting.
Specify the exponential weighting factor as a non-negative real scalar in the range [0,1]. This value determines how much weight the past data is given. A forgetting factor of 0.9 gives more weight to the older data than does a forgetting factor of 0.1. A forgetting factor of 1.0 indicates infinite memory and all the past samples are given an equal weight. A forgetting factor of 0 indicates no memory and the past samples have no weight on the current computation.
Tunable: Yes
Dependencies
To enable this parameter, set Method to Exponential
weighting and clear the Specify forgetting factor from input
port check box.
Specify the type of simulation to run. You can set this parameter to:
Interpreted execution–– Simulate model using the MATLAB® interpreter. This option shortens startup time.Code generation–– Simulate model using generated C code. The first time you run a simulation, Simulink generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
In the sliding window method, the output for each input sample is the average of the current sample and Len – 1 previous samples. Len is the length of the window in samples. To compute the first output sample, the algorithm waits until it receives the hop size number of input samples. Hop size is defined as window length – overlap length. Remaining samples in the window are considered to be zero. As an example, if the window length is 5 and the overlap length is 2, then the algorithm waits until it receives 3 samples of input to compute the first sample of the output. After generating the first output, it generates the subsequent output samples for every hop size number of input samples.
When you do not specify the window length, the algorithm chooses an infinite window length. In this mode, the output is the moving average of the current sample and all the previous samples in the channel.
For an example, see Sliding Window Method and Exponential Weighting Method.
In the exponential weighting method, the moving average is computed recursively using these formulas:
— Moving average at the current sample
— Current data input sample
— Moving average at the previous sample
λ — Forgetting factor
— Weighting factor applied to the current data sample
— Effect of the previous data on the average
For the first sample, where N = 1, the algorithm chooses = 1. For the next sample, the weighting factor is updated and used to compute the average, as per the recursive equation. As the age of the data increases, the magnitude of the weighting factor decreases exponentially and never reaches zero. In other words, the recent data has more influence on the current average than the older data.
The value of the forgetting factor determines the rate of change of the weighting factors. A forgetting factor of 0.9 gives more weight to the older data than does a forgetting factor of 0.1. A forgetting factor of 1.0 indicates infinite memory. All the previous samples are given an equal weight.
For an example, see Sliding Window Method and Exponential Weighting Method.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2016bYou can now specify a forgetting factor of 0 in the Moving Average block.
The default value of the Simulate using parameter is now
Interpreted execution. With this change, the block uses the
MATLAB interpreter for simulation by default.
Starting in R2022b, you can specify the overlap length between sliding windows using the Overlap length parameter.
Moving Average block supports input signals with arbitrary frame lengths when the:
Input signal is a fixed-size signal (frame length does not change during simulation). If Allow arbitrary frame length for fixed-size input signals is enabled, select the parameter.
Input signal is a variable-size signal (frame length changes during simulation).
When this block supports an arbitrary frame length input signal, the input frame length does not have to be a multiple of the hop size.
See Also
Blocks
- Moving RMS | Moving Maximum | Moving Minimum | Moving Standard Deviation | Moving Variance | Median Filter
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)