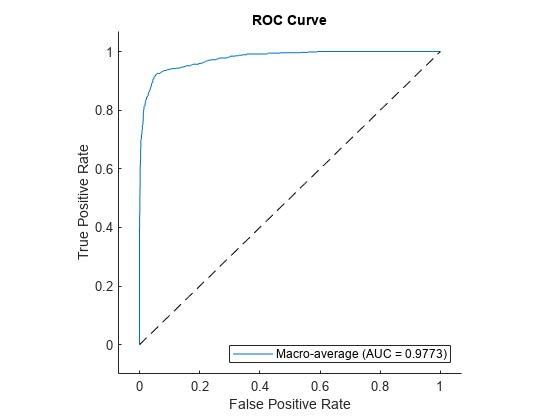
average

Compute performance metrics for average receiver operating characteristic (ROC) curve in multiclass problem

Since R2022b

Syntax

[FPR,TPR,Thresholds,AUC] = average(rocObj,type)

[avg1,avg2,Thresholds,AUC] = average(rocObj,type,metric1,metric2)

Description

[FPR,TPR,Thresholds,AUC] = average(rocObj,type) computes the averages of performance metrics stored in the rocmetrics object rocObj for a multiclass classification problem using the averaging method specified in type. The function returns the average false positive rate (FPR) and the average true positive rate (TPR) for each threshold value in Thresholds. The function also returns AUC, the area under the ROC curve composed of FPR and TPR.

[avg1,avg2,Thresholds,AUC] = average(rocObj,type,metric1,metric2)

Examples

Find Average ROC Curve

Compute the performance metrics for a multiclass classification problem by creating a rocmetrics object, and then compute the average values for the metrics by using the average function. Plot the average ROC curve using the outputs of average.

Load a sample of true labels and the prediction scores for a classification problem. For this example, there are five classes: daisy, dandelion, roses, sunflowers, and tulips. The class names are stored in classNames. The scores are the softmax prediction scores generated using the predict function. scores is an N-by-K array where N is the number of observations and K is the number of classes. The column order of scores follows the class order stored in classNames.

load('flowersDataResponses.mat')

scores = flowersData.scores;
trueLabels = flowersData.trueLabels;

classNames = flowersData.classNames;

Create a rocmetrics object by using the true labels in trueLabels and the classification scores in scores. Specify the column order of scores using classNames.

rocObj = rocmetrics(trueLabels,scores,classNames);

rocmetrics computes the FPR and TPR at different thresholds and finds the AUC value for each class.

Compute the average performance metric values, including the FPR and TPR at different thresholds and the AUC value, using the macro-averaging method.

[FPR,TPR,Thresholds,AUC] = average(rocObj,"macro");

Plot the average ROC curve, which by default displays the average AUC value.

plot(rocObj,AverageCurveType="macro",ClassNames=[])

To see the ROC curves for all the classes, do not specify the ClassNames name-value argument as [].

plot(rocObj,AverageCurveType="macro")

Obtain Macro Averages for Two Metrics

Load the fisheriris data set. The matrix meas contains flower measurements for 150 different flowers. The vector species lists the species for each flower. species contains three distinct flower names.

Train a classification tree that classifies observations into one of the three labels.

load fisheriris
mdl = fitctree(meas,species);

Create a rocmetrics object from the classification tree model.

roc = rocmetrics(mdl,meas,species); % Input data meas and response species required

Obtain the average macro recall and precision statistics in addition to the threshold and AUC statistics.

[avgRecall,avgPrec,thresh,AUC] = average(roc,"macro","recall","precision")

avgRecall = 9×1

         0
    0.6533
    0.9533
    0.9800
    0.9933
    0.9933
    1.0000
    1.0000
    1.0000

avgPrec = 9×1

       NaN
    1.0000
    0.9929
    0.9811
    0.9560
    0.9203
    0.7804
    0.6462
    0.3333

thresh = 9×1

    1.0000
    1.0000
    0.9565
    0.3333
   -0.3333
   -0.6667
   -0.9565
   -0.9783
   -1.0000

AUC = 
0.9972

Plot the ROC curve for the recall and precision metrics.

plot(roc,AverageCurveType="macro",XAxisMetric="recall",YAxisMetric="precision")

Input Arguments

rocObj — Object evaluating classification performance

rocmetrics object

Object evaluating classification performance, specified as a rocmetrics object.

type — Averaging method

"micro" | "macro" | "weighted"

Averaging method, specified as "micro", "macro", or "weighted".

• "micro" (micro-averaging) — average finds the average performance metrics by treating all one-versus-all binary classification problems as one binary classification problem. The function computes the confusion matrix components for the combined binary classification problem, and then computes the average metrics (as specified by the XAxisMetric and YAxisMetric name-value arguments) using the values of the confusion matrix.

• "macro" (macro-averaging) — average computes the average values for the metrics by averaging the values of all one-versus-all binary classification problems.

• "weighted" (weighted macro-averaging) — average computes the weighted average values for the metrics using the macro-averaging method and using the prior class probabilities (the Prior property of rocObj) as weights.

The algorithm type determines the length of the vectors for the output arguments (FPR, TPR, and Thresholds). For more details, see Average of Performance Metrics.

Data Types: char | string

metric1 — Name of metric to average

"FalsePositiveRate" (default) | name in rocObj.Metrics | name of built-in metric

Since R2024b

Name of a metric to average, specified as a name in rocObj.Metrics or as the name of a built-in metric listed in this table.

Name	Description
"TruePositives" or "tp"	Number of true positives (TP)
"FalseNegatives" or "fn"	Number of false negatives (FN)
"FalsePositives" or "fp"	Number of false positives (FP)
"TrueNegatives" or "tn"	Number of true negatives (TN)
"SumOfTrueAndFalsePositives" or "tp+fp"	Sum of TP and FP
"RateOfPositivePredictions" or "rpp"	Rate of positive predictions (RPP), (TP+FP)/(TP+FN+FP+TN)
"RateOfNegativePredictions" or "rnp"	Rate of negative predictions (RNP), (TN+FN)/(TP+FN+FP+TN)
"Accuracy" or "accu"	Accuracy, (TP+TN)/(TP+FN+FP+TN)
"TruePositiveRate", "tpr", or "recall"	True positive rate (TPR), also known as recall or sensitivity, TP/(TP+FN)
"FalseNegativeRate", "fnr", or "miss"	False negative rate (FNR), or miss rate, FN/(TP+FN)
"FalsePositiveRate" or "fpr"	False positive rate (FPR), also known as fallout or 1-specificity, FP/(TN+FP)
"TrueNegativeRate", "tnr", or "spec"	True negative rate (TNR), or specificity, TN/(TN+FP)
"PositivePredictiveValue", "ppv", "prec", or "precision"	Positive predictive value (PPV), or precision, TP/(TP+FP)
"NegativePredictiveValue" or "npv"	Negative predictive value (NPV), TN/(TN+FN)
"f1score"	F1 score, 2*TP/(2*TP+FP+FN)
"ExpectedCost" or "ecost"	Expected cost, (TP*cost(P|P)+FN*cost(N|P)+FP*cost(P|N)+TN*cost(N|N))/(TP+FN+FP+TN), where cost is a 2-by-2 misclassification cost matrix containing [0,cost(N|P);cost(P|N),0]. cost(N|P) is the cost of misclassifying a positive class (P) as a negative class (N), and cost(P|N) is the cost of misclassifying a negative class as a positive class. The software converts the K-by-K matrix specified by the Cost name-value argument of rocmetrics to a 2-by-2 matrix for each one-versus-all binary problem. For details, see Misclassification Cost Matrix.

Data Types: char | string

metric2 — Name of metric to average

"TruePositiveRate" (default) | name in rocObj.Metrics | name of a built-in metric

Since R2024b

Name of a metric to average, specified as a name in rocObj.Metrics or as the name of a built-in metric listed in this table.

Name	Description
"TruePositives" or "tp"	Number of true positives (TP)
"FalseNegatives" or "fn"	Number of false negatives (FN)
"FalsePositives" or "fp"	Number of false positives (FP)
"TrueNegatives" or "tn"	Number of true negatives (TN)
"SumOfTrueAndFalsePositives" or "tp+fp"	Sum of TP and FP
"RateOfPositivePredictions" or "rpp"	Rate of positive predictions (RPP), (TP+FP)/(TP+FN+FP+TN)
"RateOfNegativePredictions" or "rnp"	Rate of negative predictions (RNP), (TN+FN)/(TP+FN+FP+TN)
"Accuracy" or "accu"	Accuracy, (TP+TN)/(TP+FN+FP+TN)
"TruePositiveRate", "tpr", or "recall"	True positive rate (TPR), also known as recall or sensitivity, TP/(TP+FN)
"FalseNegativeRate", "fnr", or "miss"	False negative rate (FNR), or miss rate, FN/(TP+FN)
"FalsePositiveRate" or "fpr"	False positive rate (FPR), also known as fallout or 1-specificity, FP/(TN+FP)
"TrueNegativeRate", "tnr", or "spec"	True negative rate (TNR), or specificity, TN/(TN+FP)
"PositivePredictiveValue", "ppv", "prec", or "precision"	Positive predictive value (PPV), or precision, TP/(TP+FP)
"NegativePredictiveValue" or "npv"	Negative predictive value (NPV), TN/(TN+FN)
"f1score"	F1 score, 2*TP/(2*TP+FP+FN)
"ExpectedCost" or "ecost"	Expected cost, (TP*cost(P|P)+FN*cost(N|P)+FP*cost(P|N)+TN*cost(N|N))/(TP+FN+FP+TN), where cost is a 2-by-2 misclassification cost matrix containing [0,cost(N|P);cost(P|N),0]. cost(N|P) is the cost of misclassifying a positive class (P) as a negative class (N), and cost(P|N) is the cost of misclassifying a negative class as a positive class. The software converts the K-by-K matrix specified by the Cost name-value argument of rocmetrics to a 2-by-2 matrix for each one-versus-all binary problem. For details, see Misclassification Cost Matrix.

Data Types: char | string

Output Arguments

FPR — Average false positive rates

numeric vector

Average false positive rates, returned as a numeric vector.

TPR — Average true positive rates

numeric vector

Average true positive rates, returned as a numeric vector.

Thresholds — Thresholds on classification scores

numeric vector

Thresholds on classification scores at which the function finds each of the average performance metric values (FPR and TPR), returned as a vector.

AUC — Area under average ROC curve

numeric scalar

Area under the average ROC curve composed of FPR and TPR, returned as a numeric scalar.

avg1 — Average of metric1

double or single vector

Since R2024b

Average of metric1, returned as a double or single vector, depending on the data.

avg2 — Average of metric2

double or single vector

Since R2024b

Average of metric2, returned as a double or single vector, depending on the data.

More About

Receiver Operating Characteristic (ROC) Curve

A ROC curve shows the true positive rate versus the false positive rate for different thresholds of classification scores.

The true positive rate and the false positive rate are defined as follows:

• True positive rate (TPR), also known as recall or sensitivity — TP/(TP+FN), where TP is the number of true positives and FN is the number of false negatives

• False positive rate (FPR), also known as fallout or 1-specificity — FP/(TN+FP), where FP is the number of false positives and TN is the number of true negatives

Each point on a ROC curve corresponds to a pair of TPR and FPR values for a specific threshold value. You can find different pairs of TPR and FPR values by varying the threshold value, and then create a ROC curve using the pairs. For each class, rocmetrics uses all distinct adjusted score values as threshold values to create a ROC curve.

For a multiclass classification problem, rocmetrics formulates a set of one-versus-all binary classification problems to have one binary problem for each class, and finds a ROC curve for each class using the corresponding binary problem. Each binary problem assumes one class as positive and the rest as negative.

For a binary classification problem, if you specify the classification scores as a matrix, rocmetrics formulates two one-versus-all binary classification problems. Each of these problems treats one class as a positive class and the other class as a negative class, and rocmetrics finds two ROC curves. Use one of the curves to evaluate the binary classification problem.

For more details, see ROC Curve and Performance Metrics.

Area Under ROC Curve (AUC)

The area under a ROC curve (AUC) corresponds to the integral of a ROC curve (TPR values) with respect to FPR from FPR = 0 to FPR = 1.

The AUC provides an aggregate performance measure across all possible thresholds. The AUC values are in the range 0 to 1, and larger AUC values indicate better classifier performance.

One-Versus-All (OVA) Coding Design

The one-versus-all (OVA) coding design reduces a multiclass classification problem to a set of binary classification problems. In this coding design, each binary classification treats one class as positive and the rest of the classes as negative. rocmetrics uses the OVA coding design for multiclass classification and evaluates the performance on each class by using the binary classification that the class is positive.

For example, the OVA coding design for three classes formulates three binary classifications:

$$\begin{array}{cccc}& \text{Binary 1}& \text{Binary }2& \text{Binary 3}\\ \text{Class 1}& 1& -1& -1\\ \text{Class 2}& -1& 1& -1\\ \text{Class 3}& -1& -1& 1\end{array}$$

Each row corresponds to a class, and each column corresponds to a binary classification problem. The first binary classification assumes that class 1 is a positive class and the rest of the classes are negative. rocmetrics evaluates the performance on the first class by using the first binary classification problem.

Algorithms

Adjusted Scores for Multiclass Classification Problem

For each class, rocmetrics adjusts the classification scores (input argument Scores of rocmetrics) relative to the scores for the rest of the classes if you specify Scores as a matrix. Specifically, the adjusted score for a class given an observation is the difference between the score for the class and the maximum value of the scores for the rest of the classes.

For example, if you have [s₁,s₂,s₃] in a row of Scores for a classification problem with three classes, the adjusted score values are [s₁-max(s₂,s₃),s₂-max(s₁,s₃),s₃-max(s₁,s₂)].

rocmetrics computes the performance metrics using the adjusted score values for each class.

For a binary classification problem, you can specify Scores as a two-column matrix or a column vector. Using a two-column matrix is a simpler option because the predict function of a classification object returns classification scores as a matrix, which you can pass to rocmetrics. If you pass scores in a two-column matrix, rocmetrics adjusts scores in the same way that it adjusts scores for multiclass classification, and it computes performance metrics for both classes. You can use the metric values for one of the two classes to evaluate the binary classification problem. The metric values for a class returned by rocmetrics when you pass a two-column matrix are equivalent to the metric values returned by rocmetrics when you specify classification scores for the class as a column vector.

Alternative Functionality

• You can use the plot function to create the average ROC curve. The function returns a ROCCurve object containing the XData, YData, Thresholds, and AUC properties, which correspond to the output arguments FPR, TPR, Thresholds, and AUC of the average function, respectively. For an example, see Plot ROC Curve.

References

[1] Sebastiani, Fabrizio. "Machine Learning in Automated Text Categorization." ACM Computing Surveys 34, no. 1 (March 2002): 1–47.

Version History

Introduced in R2022b

R2024b: average supports the average of any two metrics

You can compute and plot the rocmetrics average results of any two metrics simultaneously. For an example, see Obtain Macro Averages for Two Metrics.