TPC Decoder
Turbo product code (TPC) decoder
Libraries:
Communications Toolbox /
Error Detection and Correction /
Block
Description
The TPC Decoder block performs 2-D turbo product code (TPC) decoding of the soft input LLRs corresponding to the product code iteratively, using Chase-Pyndiah algorithm. The product code is a 2-D concatenation of linear block codes. The linear block code can be a parity check code, a Hamming code, or a BCH code capable of correcting two errors. Extended and shortened codes can be applied independently on each dimension. For a description of 2-D TPC decoding, see Turbo Product Code Decoding.
For information about valid code pairs and the error-correcting capability for each valid code pair, see Component Code Pairs.
Examples
Perform error rate calculations for a transmission signal that has been TPC encoded and decoded.
A random signal is TPC encoded, QPSK modulated, filtered through an AWGN channel, and QPSK demodulated. The bipolar mapping is converted from negative to positive mapping and then the signal is TPC decoded. An error rate calculation compares the original message to the recovered message.
Open Example Model and Explore Its Contents
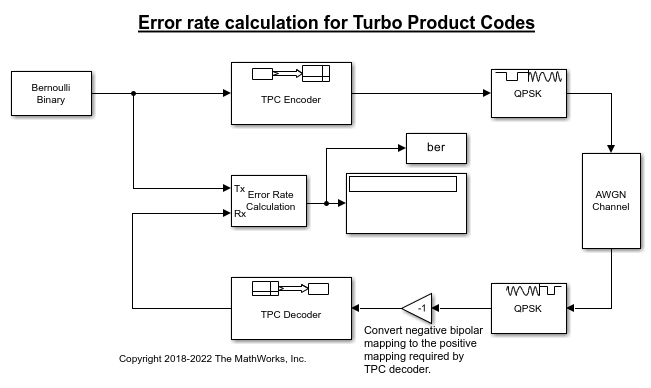
Several settings must be aligned with each other to synchronize encoding and decoding of the message. Start by deciding on a code rate, and aligning the TPC Encoder and TPC Decoder 2-D [N,K] pairs. For this example the default settings are used, [Nr,Kr] = [15,11] and [Nc,Kc] = [32,26].
The number of samples per frame and the sample time used by the Bernoulli Binary Generator block are determined based on the message length parameters, Number of rows in message, Kr and Number of columns in message, Kc.
Number of samples per frame = (Kr*Kc) = 286
Sample time = 1/(Kr*Kc) = 0.0035.
The white Gaussian noise the SNR setting is calculated based on the coding rate, modulation order, and Eb/N0.
Modulation order, M = 2
Eb/N0 = -11
rate = (Kr*Kc)/((Nr-Kr)*(Nc-Kc)) = 14.3
snr = 10*log10(M*rate*10^(ebn0/10)) = 3.5637
The noise variance used in the QPSK Demodulator Baseband block is calculated based on the SNR.
Noise variance = 1/10^(snr/10) = 1/10^(3.5637/10) = 0.4402
Run the model and observe the error rate calculation. Results will vary from run to run due to the use of random input data.
Bit error rate: 0.00042
Further Exploration
To run the model yourself, open the example using the button provided or by entering open slex_tpc_err_rate_calc at the MATLAB® command prompt. Consider modifying the model to change the signal to noise ratio. When adjusting TPC Encoder settings be sure to align settings in the TPC Decoder, Bernoulli Binary Generator, AWGN Channel, and QPSK Demodulator Baseband.
Ports
Input
Log likelihood ratios, specified as a column vector.
For full-length input messages, the length of the column vector is the product of Number of rows in code, Nr and Number of columns in code, Nc.
For shortened input messages, the length of the column vector is the product of (NR–KR+SR) and (NC–KC+SC), where:
NR is the value of Number of rows in code, Nr.
KR is the value of Number of rows in message, Kr.
SR is the value of Number of rows in shortened message, Sr.
NC is the value of Number of columns in code, Nc.
KC is the value of Number of columns in message, Kc.
SC is the value of Number of columns in shortened message, Sc.
Data Types: double | single
Output
TPC decoded message, returned as a column vector of binary values.
For full-length input messages, the length of the column vector is the product of Number of rows in message, Kr and Number of columns in message, Kc.
For shortened input messages, the length of the column vector is the product of Number of rows in shortened message, Sr and Number of columns in shortened message, Sc.
Data Types: Boolean
Actual number of decoding iterations, returned as a positive integer.
Dependencies
To enable this port, select Output number of iterations executed.
Data Types: double
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Row TPC parameters
When Extended codes is selected, the lists for Number of rows in code, Nr and Number of rows in message, Kr contain the valid values for extended individual code pairs (NR,KR).
When Extended codes is cleared, the lists for Number of rows in code, Nr and Number of rows in message, Kr contain the valid values for nonextended individual code pairs (NR,KR).
Number of rows in the product code matrix, NR. The list of integer values varies depending on the setting for Extended codes.
Number of rows in the message matrix, KR. The list of integer values varies depending on the setting for Extended codes and Number of rows in code, Nr.
Select Specify shortened message length to specify a value for Number of rows in shortened message, Sr.
Number of rows in the shortened message matrix, SR, specified as an integer less than or equal to KR. When you specify this parameter, provide full-length NR and KR values to specify the (NR,KR) code pair. This code pair is then shortened to the (NR–KR+SR,SR) code pair, where:
NR is the value of Number of rows in code, Nr.
KR is the value of Number of rows in message, Kr.
SR is the value of Number of rows in shortened message, Sr.
Dependencies
To enable this parameter, select Specify shortened message length.
Column TPC parameters
When Extended codes is selected, the lists for Number of columns in code, Nc and Number of columns in message, Kc contain the valid values for extended individual code pairs (NC,KC).
When Extended codes is cleared, the lists for Number of columns in code, Nc and Number of columns in message, Kc contain the valid values for nonextended individual code pairs (NC,KC).
Number of columns in the product code matrix, NC. The list of integer values varies depending on the setting for Extended codes.
Number of columns in the message matrix, KC. The list of integer values varies depending on the setting for Extended codes and Number of columns in code, Nc.
Select Specify shortened message length to specify a value for Number of columns in shortened message, Sc.
Number of columns in the shortened message matrix, SC, specified as an integer. When you specify this parameter, provide full-length NC and KC values to specify the (NC,KC) code pair. This code pair is then shortened to the (NC–KC+SC, SC) code pair, where:
NC is the value of Number of columns in code, Nc.
KC is the value of Number of columns in message, Kc.
SC is the value of Number of columns in shortened message, Sc.
Dependencies
To enable this parameter, select Specify shortened message length.
Maximum number of decoding iterations, specified as a positive integer.
Select Stop iterating when code converges to terminate decoding early if the calculated syndrome or parity-check of the component code evaluates to zero before Maximum number of iterations.
Select this parameter to add the Iter output
port and output the actual number of TPC decoding iterations performed.
Type of simulation to run, specified as Code generation or
Interpreted execution.
Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
This table lists the supported component code pairs for the row (NR,KR) and column (NC,KC) parameters.
NR and KR represent the number of rows in the product code matrix and message matrix, respectively.
NC and KC represent the number of columns in the product code matrix and message matrix, respectively.
Within each code type, any two component code pairs can form a 2-D TPC code. The table also includes the error-correction capability for each code pair.
| Code type | Component Code Pairs(NR,KR) and (NC,KC) | Error-Correction Capability (T) |
| Hamming code | (255,247) | 1 |
| (127,120) | 1 | |
| (63,57) | 1 | |
| (31,26) | 1 | |
| (15,11) | 1 | |
| (7,4) | 1 | |
| Extended Hamming code | (256,247) | 1 |
| (128,120) | 1 | |
| (64,57) | 1 | |
| (32,26) | 1 | |
| (16,11) | 1 | |
| (8,4) | 1 | |
| BCH code | (255,239) | 2 |
| (127,113) | 2 | |
| (63,51) | 2 | |
| (31,21) | 2 | |
| (15,7) | 2 | |
| Extended BCH code | (256,239) | 2 |
| (128,113) | 2 | |
| (64,51) | 2 | |
| (32,21) | 2 | |
| (16,7) | 2 | |
| Parity check code | (256,255) | - |
| (128,127) | - | |
| (64,63) | - | |
| (32,31) | - | |
| (16,15) | - | |
| (8,7) | - | |
| (4,3) | - |
Turbo product codes (TPC) are a form of concatenated codes used as forward error correcting (FEC) codes. Two or more component block codes, such as systematic linear block codes, are used to construct TPCs. The TPC decoder achieves near-optimum decoding of product codes using Chase decoding and the Pyndiah algorithm to perform iterative soft input, soft output decoding. For a detailed description, see [1] and [2]. This decoder implements an iterative soft input, soft output 2-D product code decoding, as described in [2], using two Linear Block Codes. The decoder expects the soft bit log likelihood ratios (LLRs) obtained from digital demodulation as the input signal.
The TPC decoder accepts either full-length or shortened codes.
 TPC Decoding Full-Length Messages
TPC Decoding Full-Length Messages
TPC encoded full-length input messages are decoded using specified 2-D TPC code pairs. Row-wise decoding uses the (NC,KC) code pair and column-wise decoding uses the (NR,KR) code pair. The input vector length must be NR × NC. To perform the 2-D TPC decoding, the column vector of the input LLRs, composed of the message and parity bits, is arranged into an NR-by-NC matrix.

The TPC decoder achieves near-optimum decoding of product codes using Chase decoding and the Pyndiah algorithm to perform iterative soft input, soft output decoding. Chase decoding forms a set of possible codewords for each row or column. The Pyndiah algorithm calculates soft information required for the next decoding step.
Iterative Soft Input, Soft Output Decoder
The iterative soft input, soft output decoding, as shown in the block diagram, carries out two decoding steps for each iteration.

The soft inputs for decoding are R(m) = R + α(m)W(m).
Iteration loop counter i increments from i = 1 to the specified number of iterations.
m =
2i –1is the decoding step index.R is the received LLR matrix.
R(m) is the soft input for the mth decoding step.
W(m) is the input extrinsic information for the mth decoding step.
α(m) = [0,0.2,0.3,0.5,0.7,0.9,1,1, ...], where α is a weighting factor applied based on the decoding step index. For higher decoding steps, α = 1.
β(m) = [0.2,0.4,0.6,0.8,1,1, ...], where β is a reliability factor applied based on the decoding step index. For higher decoding steps, β = 1.
D contains the decoded message bits. The output message bits are formed from D by mapping –1 to 0 and +1 to 1, then reshaping the message block into a column vector.
The output message bits are formed after iterating through the specified number of iterations, or, if early termination is enabled, after code convergence.
Early Termination of TPC Decoding
If early termination is enabled, a code convergence check is performed on the hard decision of the soft input in each row-wise and column-wise decoding step. Early termination can be triggered after either the row-wise decoding or column-wise decoding converges.

The code is converged if, for all rows or all columns,
The syndrome evaluates to zero in the codes (Hamming codes, Extended Hamming codes, BCH codes, or Extended BCH codes).
The parity check is evaluated to zero in parity check codes.
The reported number of iterations evaluates to the iteration value that is currently in progress. For example, if the code convergence check is satisfied after row-wise decoding in the third iteration (after 2.5 decoding steps), then the number of iteration returned is 3.
 TPC Decoding Shortened Messages
TPC Decoding Shortened Messages
TPC encoded shortened input messages are decoded using specified 2-D TPC code pairs. Row-wise decoding uses the (NC – KC + SC, SC) code pair and column-wise decoding uses the (NR – KR + SR, SR) code pair. The input vector length must be (NR – KR + SR) × (NC– KC + SC). To perform the 2-D TPC decoding of shortened messages, the column vector of the input LLRs, composed of the shortened message and parity bits, is arranged into an (NR – KR + SR)-by-(NC – KC + SC) matrix.
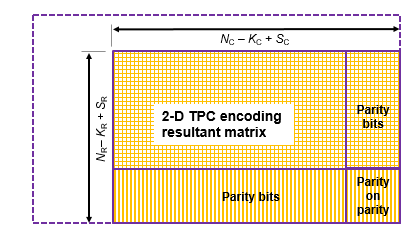
The TPC decoder processes the received shortened message LLRs similar to full length codes, with these exceptions:
The shortened bit positions in the received codeword are set to –1.
The Chase algorithm does not consider the shortened bit positions while choosing the least reliable bits.
References
[1] Chase, D. "Class of Algorithms for Decoding Block Codes with Channel Measurement Information." IEEE Transactions on Information Theory, Volume 18, Number 1, January 1972, pp. 170–182.
[2] Pyndiah, R. M. "Near-Optimum Decoding of Product Codes: Block Turbo Codes." IEEE Transactions on Communications. Vol. 46, Number 8, August 1998, pp. 1003–1010.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2018b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
웹사이트 선택
번역된 콘텐츠를 보고 지역별 이벤트와 혜택을 살펴보려면 웹사이트를 선택하십시오. 현재 계신 지역에 따라 다음 웹사이트를 권장합니다:
또한 다음 목록에서 웹사이트를 선택하실 수도 있습니다.
사이트 성능 최적화 방법
최고의 사이트 성능을 위해 중국 사이트(중국어 또는 영어)를 선택하십시오. 현재 계신 지역에서는 다른 국가의 MathWorks 사이트 방문이 최적화되지 않았습니다.
미주
- América Latina (Español)
- Canada (English)
- United States (English)
유럽
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)