tpcdec

Turbo product code (TPC) decoder

Syntax

decoded = tpcdec(llr,N,K)

decoded = tpcdec(llr,N,K,S)

decoded = tpcdec(llr,N,K,S,maxnumiter)

decoded = tpcdec(llr,N,K,S,maxnumiter,earlyterm)

[decoded,actualnumiter] = tpcdec(___)

Description

decoded = tpcdec(llr,N,K) performs 2-D TPC decoding on input log likelihood ratios, llr, using two linear block codes specified by codeword length N and message length K. For a description of 2-D TPC decoding, see Turbo Product Code Decoding.

decoded = tpcdec(llr,N,K,S) performs 2-D TPC decoding on the shortened llr using a 2-D TPC decoder specified by codeword length (N–K+S) and message length S.

decoded = tpcdec(llr,N,K,S,maxnumiter) performs 2-D TPC decoding for maxnumiter iterations. To use maxnumiter with full-length messages, specify S as empty, [ ].

decoded = tpcdec(llr,N,K,S,maxnumiter,earlyterm) performs 2-D TPC decoding and terminates early if the calculated syndrome or parity-check of the component code evaluates to zero before maxnumiter decoding iterations. To use maxnumiter and earlyterm with full-length messages, specify S as empty, [ ].

[decoded,actualnumiter] = tpcdec(___)also returns the actual number of decoding iterations after performing 2-D TPC decoding using any of the prior syntaxes.

Examples

Decode Using Full-Length TPC Codes

Decode an approximate log-likelihood ratio output signal from 16-QAM demodulation.

Begin by encoding a random bit vector using 2-D turbo product coding (TPC) with extended Hamming codes and extended BCH codes.

Specify the (N,K) code pairs to use for TPC encoding.

N = [32;16]; 
K = [21;11]; 

Generate a column vector of random message bits and TPC-encode the message. Specify the message bits as a vector with length equal to the product of the elements in K.

msg = randi([0 1],prod(K),1);
code = tpcenc(msg,N,K);

Apply 16-QAM modulation. Add AWGN to the signal. Demodulate the signal, outputting approximate LLRs.

M = 16;
snr = 10;

txsig = qammod(code,M,'InputType','bit', ...
    'UnitAveragePower',true);

rxsig = awgn(txsig,snr,'measured');

llr = qamdemod(rxsig,M,'OutputType','approxllr', ...
    'UnitAveragePower',true,'NoiseVariance',10.^(-snr/10));

Perform TPC decoding using three iterations. Because the demodulator output is negative bipolar mapped and TPC decoder expects positive bipolar mapped input, the demodulated signal output must be negated at the decoder input. Check the number of bit errors in the decoded signal.

iterations = 3;
decoded = tpcdec(-llr,N,K,[],iterations);

numerr = biterr(msg,decoded)

numerr = 0

Decode Using Shortened TPC Codes

Decode a shortened TPC code. Apply QPSK modulation and output the approximate log-likelihood ratio signal obtained from QPSK demodulation.

Begin by encoding a random bit vector using 2-D turbo product coding (TPC) with extended Hamming codes and extended BCH codes.

Specify (N,K) code pairs and S for TPC encoding.

N = [32;32];
K = [21;26];
S = [19;24];

Generate a column vector of random message bits and TPC-encode the message. Specify the shortened message bits as a vector with length equal to the product of the elements in S.

msg = randi([0 1],prod(S),1);
code = tpcenc(msg,N,K,S);

Apply QPSK modulation. Add AWGN to the signal. Demodulate the signal and output approximate LLRs.

M = 4;
snr = 3;

txsig = qammod(code,M,'InputType','bit', ...
    'UnitAveragePower',true);

rxsig = awgn(txsig,snr,'measured');

llr = qamdemod(rxsig,M,'OutputType','approxllr', ...
    'UnitAveragePower',true,'NoiseVariance',10.^(-snr/10));

Perform TPC decoding using two iterations. Because the demodulator output is negative bipolar mapped and TPC decoder expects positive bipolar mapped input, the demodulated signal output must be negated at the decoder input. Check the bit error rate of the decoded signal.

iterations = 2;
decoded = tpcdec(-llr,N,K,S,iterations);

[~,ber] = biterr(msg,decoded)

ber = 0

TPC Decoding with Shortening and Early Termination

Decode a shortened TPC code and specify early termination of decoding. Apply QPSK modulation and output the approximate log-likelihood ratio signal obtained from QPSK demodulation.

Begin by encoding a random bit vector using 2-D turbo product coding (TPC) with extended Hamming codes and extended BCH codes. Specify (N,K) code pairs and S for TPC encoding, and a maximum of 10 decoding iterations. Perform QPSK modulation on the signal.

n = [64; 32];
k = [51; 26];
s = [49; 24];
maxnumiter = 10;
M = 4;

msg = randi([0 1],prod(s),1);  % Random bits
code = tpcenc(msg,n,k,s);

txsig = qammod(code,M,'InputType','bit', ...
    'UnitAveragePower',true);

Add noise to the transmitted signal.

snr = 5;
rxsig = awgn(txsig,snr,'measured');

Demodulate the received signal using approximate LLR demapping.

llr = qamdemod(rxsig,M,'OutputType', ...
    'approxllr','UnitAveragePower',true, ...
    'NoiseVariance',10.^(-snr/10));

Specify the maximum number of TPC decoding iterations and return the actual number of iterations performed. Early termination of the TPC decoding is on by default. Display the number of errors and the number of iterations performed.

[decoded,actualNumIter] = tpcdec(-llr,n,k,s,maxnumiter);
numErr = biterr(msg,decoded);
disp(['Terminated after ' num2str(actualNumIter) ' iterations.' ...
    ' Number of errors = ' num2str(numErr) '.']);

Terminated after 4 iterations. Number of errors = 0.

Input Arguments

llr — Log likelihood ratios

column vector

Log likelihood ratios, specified as a column vector.

• For full-length codes, the length of the input column vector is the product of the elements in N.

• For shortened codes, the length of the input column vector is the product of the elements in (N–K+S).

Data Types: double | single

N — Codeword length

two-element integer vector

Codeword length, specified as a two-element integer vector, [N_R; N_C]. N_R represents the number of rows in the product code matrix. N_C represents the number of columns in the product code matrix. For more information about N_R and N_C, see Turbo Product Code Decoding. For a list of valid (N(i), K(i)) code pairs, see More About.

Data Types: double

K — Message length

two-element integer vector

Message length, specified as a two-element integer vector, [K_R; K_C]. For a full-length message, the input column vector containing the input LLRs is arranged into a K_R-by-K_C matrix. K_R represents the number of rows in the message matrix. K_C represents the number of columns in the message matrix. For more information about K_R and K_C, see Turbo Product Code Decoding. For a list of valid (N(i), K(i)) code pairs, see More About.

Data Types: double

S — Shortened message length

two-element integer vector

Shortened message length, specified as a two-element integer vector, [S_R; S_C]. For a shortened message, the input column vector containing the input LLRs is arranged into an S_R-by-S_C matrix. S_R represents the number of rows in the matrix. S_C represents the number of columns in the matrix. For more information about S_R and S_C, see Turbo Product Code Decoding.

When you specify this parameter, specify N and K vectors for the full-length TPC codes that are shortened to (N(i) – K(i) + S(i), S(i)) codes.

Data Types: double

maxnumiter — Maximum number of decoding iterations

4 (default) | positive integer

Maximum number of decoding iterations, specified as a positive integer.

Data Types: double

earlyterm — Enable early termination

true (default) | false

Enable early termination of decoding, specified as a logical. When earlyterm is true the decoding terminates early if the calculated syndrome or parity-check of the component code evaluates to zero before maxnumiter decoding iterations.

Data Types: double

Output Arguments

decoded — TPC decoded message

column vector

TPC decoded message, returned as a column vector.

• For full-length codes, the length of the returned column vector is the product of the elements in K.

• For shortened codes, the length of the returned column vector is the product of the elements in S.

Data Types: logical

actualnumiter — Actual number of decoding iterations

positive integer

Actual number of decoding iterations performed, returned as a positive integer.

Data Types: double

More About

Component Codes

This table lists the supported component code pairs for the row (N_R,K_R) and column (N_C,K_C) parameters.

• N_R and K_R represent the number of rows in the product code matrix and message matrix, respectively.

• N_C and K_C represent the number of columns in the product code matrix and message matrix, respectively.

Within each code type, any two component code pairs can form a 2-D TPC code. The table also includes the error-correction capability for each code pair.

Code type	Component Code Pairs(NR,KR) and (NC,KC)	Error-Correction Capability (T)
Hamming code	(255,247)	1
	(127,120)	1
	(63,57)	1
	(31,26)	1
	(15,11)	1
	(7,4)	1
Extended Hamming code	(256,247)	1
	(128,120)	1
	(64,57)	1
	(32,26)	1
	(16,11)	1
	(8,4)	1
BCH code	(255,239)	2
	(127,113)	2
	(63,51)	2
	(31,21)	2
	(15,7)	2
Extended BCH code	(256,239)	2
	(128,113)	2
	(64,51)	2
	(32,21)	2
	(16,7)	2
Parity check code	(256,255)	-
	(128,127)	-
	(64,63)	-
	(32,31)	-
	(16,15)	-
	(8,7)	-
	(4,3)	-

Turbo Product Code Decoding

Turbo product codes (TPC) are a form of concatenated codes used as forward error correcting (FEC) codes. Two or more component block codes, such as systematic linear block codes, are used to construct TPCs. The TPC decoder achieves near-optimum decoding of product codes using Chase decoding and the Pyndiah algorithm to perform iterative soft input, soft output decoding. For a detailed description, see [1] and [2]. This decoder implements an iterative soft input, soft output 2-D product code decoding, as described in [2], using two Linear Block Codes. The decoder expects the soft bit log likelihood ratios (LLRs) obtained from digital demodulation as the input signal.

Note

The TPC decoder expects a positive bipolar mapped input, specifically –1 mapped to 0 and +1 mapped to 1. The output from demodulators in the Communications Toolbox™ is negative bipolar mapping, specifically +1 mapped to 0 and –1 mapped to +1. Therefore, the LLR output from demodulators must be negated to provide the positive bipolar mapped input expected by the TPC decoder.

The TPC decoder decodes either full-length or shortened codes.

 TPC Decoding Full-Length Messages

TPC encoded full-length input messages are decoded using specified 2-D TPC code pairs. Row-wise decoding uses the (N_C,K_C) code pair and column-wise decoding uses the (N_R,K_R) code pair. The input vector length must be N_R × N_C. To perform the 2-D TPC decoding, the column vector of the input LLRs, composed of the message and parity bits, is arranged into an N_R-by-N_C matrix.

The TPC decoder achieves near-optimum decoding of product codes using Chase decoding and the Pyndiah algorithm to perform iterative soft input, soft output decoding. Chase decoding forms a set of possible codewords for each row or column. The Pyndiah algorithm calculates soft information required for the next decoding step.

Iterative Soft Input, Soft Output Decoder

The iterative soft input, soft output decoding, as shown in the block diagram, carries out two decoding steps for each iteration.

The soft inputs for decoding are R(m) = R + α(m)W(m).

• Iteration loop counter i increments from i = 1 to the specified number of iterations.

• m = 2i – 1 is the decoding step index.

• R is the received LLR matrix.

• R(m) is the soft input for the mth decoding step.

• W(m) is the input extrinsic information for the mth decoding step.

• α(m) = [0,0.2,0.3,0.5,0.7,0.9,1,1, ...], where α is a weighting factor applied based on the decoding step index. For higher decoding steps, α = 1.

• β(m) = [0.2,0.4,0.6,0.8,1,1, ...], where β is a reliability factor applied based on the decoding step index. For higher decoding steps, β = 1.

• D contains the decoded message bits. The output message bits are formed from D by mapping –1 to 0 and +1 to 1, then reshaping the message block into a column vector.

The output message bits are formed after iterating through the specified number of iterations, or, if early termination is enabled, after code convergence.

Early Termination of TPC Decoding

If early termination is enabled, a code convergence check is performed on the hard decision of the soft input in each row-wise and column-wise decoding step. Early termination can be triggered after either the row-wise decoding or column-wise decoding converges.

The code is converged if, for all rows or all columns,

• The syndrome evaluates to zero in the codes (Hamming codes, Extended Hamming codes, BCH codes, or Extended BCH codes).

• The parity check is evaluated to zero in parity check codes.

The reported number of iterations evaluates to the iteration value that is currently in progress. For example, if the code convergence check is satisfied after row-wise decoding in the third iteration (after 2.5 decoding steps), then the number of iteration returned is 3.

 TPC Decoding Shortened Messages

TPC encoded shortened input messages are decoded using specified 2-D TPC code pairs. Row-wise decoding uses the (N_C – K_C + S_C, S_C) code pair and column-wise decoding uses the (N_R – K_R + S_R, S_R) code pair. The input vector length must be (N_R – K_R + S_R) × (N_C– K_C + S_C). To perform the 2-D TPC decoding of shortened messages, the column vector of the input LLRs, composed of the shortened message and parity bits, is arranged into an (N_R – K_R + S_R)-by-(N_C – K_C + S_C) matrix.

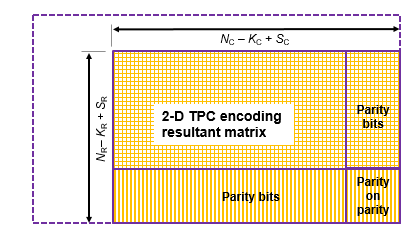
The TPC decoder processes the received shortened message LLRs similar to full length codes, with these exceptions:

• The shortened bit positions in the received codeword are set to –1.

• The Chase algorithm does not consider the shortened bit positions while choosing the least reliable bits.

References

[1] Chase, D. "Class of Algorithms for Decoding Block Codes with Channel Measurement Information." IEEE Transactions on Information Theory, Volume 18, Number 1, January 1972, pp. 170–182.

[2] Pyndiah, R. M. "Near-Optimum Decoding of Product Codes: Block Turbo Codes." IEEE Transactions on Communications. Volume 46, Number 8, August 1998, pp. 1003–1010.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• TPC parameters N, K, and S must be constant values. If the value used for each of these parameters does not change, then you can assign them by expression or variable.

Version History

Introduced in R2018a