sph2cartvec
Convert vector from spherical basis components to Cartesian components
Description
vr = sph2cartvec(vs,az,el)vs, from their
spherical basis representation to their representation in a local
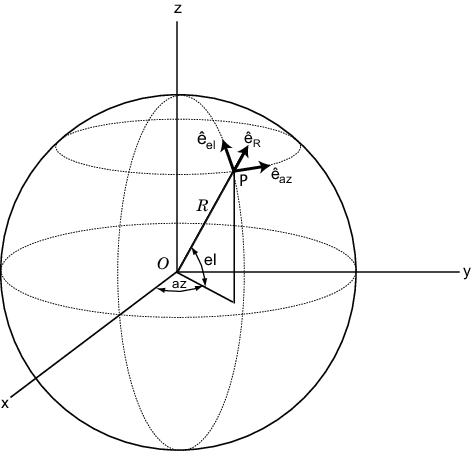
Cartesian coordinate system. A spherical basis representation is the set of components of a
vector projected into the right-handed spherical basis given by . The orientation of a spherical basis depends upon its location on the
sphere as determined by azimuth, az, and elevation,
el.
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2020a