Continuous and Discrete Wavelet Analysis of Frequency Break
This example shows the difference between the discrete wavelet transform (DWT) and the continuous wavelet transform (CWT).
When is Continuous Analysis More Appropriate than Discrete Analysis?
To answer this, consider the related questions: Do you need to know all values of a continuous decomposition to reconstruct the signal exactly? Can you perform nonredundant analysis? When the energy of the signal is finite, not all values of a decomposition are needed to exactly reconstruct the original signal, provided that you are using a wavelet that satisfies some admissibility condition. Usual wavelets satisfy this condition. In this case, a continuous-time signal is characterized by the knowledge of the discrete transform. In such cases, discrete analysis is sufficient and continuous analysis is redundant.
Continuous analysis is often easier to interpret, since its redundancy tends to reinforce the traits and makes all information more visible. This is especially true of very subtle information. Thus, the analysis gains in "readability" and in ease of interpretation what it loses in terms of saving space.
DWT and CWT of a Signal with a Frequency Break
Show how analysis using wavelets can detect the exact instant when a signal changes. Use a discontinuous signal that consists of a slow sine wave abruptly followed by a medium sine wave.
load freqbrk;
signal = freqbrk;Perform the discrete wavelet transform (DWT) at level 5 using the Haar wavelet.
lev = 5;
wname = 'db1';
nbcol = 64;
[c,l] = wavedec(signal,lev,wname);Expand discrete wavelet coefficients for plot.
len = length(signal); cfd = zeros(lev,len); for k = 1:lev d = detcoef(c,l,k); d = d(:)'; d = d(ones(1,2^k),:); cfd(k,:) = wkeep(d(:)',len); end cfd = cfd(:); I = find(abs(cfd)<sqrt(eps)); cfd(I) = zeros(size(I)); cfd = reshape(cfd,lev,len); cfd = wcodemat(cfd,nbcol,'row'); h211 = subplot(2,1,1); h211.XTick = []; plot(signal,'r'); title('Analyzed signal.'); ax = gca; ax.XLim = [1 length(signal)]; subplot(2,1,2); colormap(cool(128)); image(cfd); tics = 1:lev; labs = int2str(tics'); ax = gca; ax.YTickLabelMode = 'manual'; ax.YDir = 'normal'; ax.Box = 'On'; ax.YTick = tics; ax.YTickLabel = labs; title('Discrete Transform, absolute coefficients.'); ylabel('Level');

Perform the continuous wavelet transform (CWT) and visualize results
figure; [cfs,f] = cwt(signal,1,'waveletparameters',[3 3.1]); hp = pcolor(1:length(signal),f,abs(cfs)); hp.EdgeColor = 'none'; set(gca,'YScale','log'); xlabel('Sample'); ylabel('log10(f)');

If you just look at the finest scale CWT coefficients, you can localize the frequency change precisely.
plot(abs(cfs(1,:))); grid on;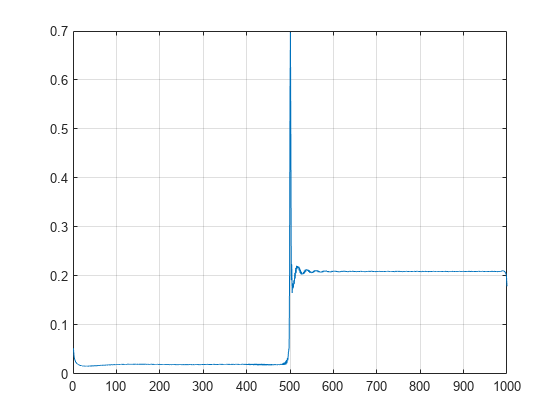
This example shows an important advantage of wavelet analysis over Fourier. If the same signal had been analyzed by the Fourier transform, we would not have been able to detect the instant when the signal's frequency changed, whereas it is clearly observable here.