Mixed-Effects Models
Introduction to Mixed-Effects Models
In statistics, an effect is anything that influences the value of a response variable at a particular setting of the predictor variables. Effects are translated into model parameters. In linear models, effects become coefficients, representing the proportional contributions of model terms. In nonlinear models, effects often have specific physical interpretations, and appear in more general nonlinear combinations.
Fixed effects represent population parameters, assumed to be the same each time data is collected. Estimating fixed effects is the traditional domain of regression modeling. Random effects, by comparison, are sample-dependent random variables. In modeling, random effects act like additional error terms, and their distributions and covariances must be specified.
For example, consider a model of the elimination of a drug from the bloodstream. The model uses time t as a predictor and the concentration of the drug C as the response. The nonlinear model term C0e–rt combines parameters C0 and r, representing, respectively, an initial concentration and an elimination rate. If data is collected across multiple individuals, it is reasonable to assume that the elimination rate is a random variable ri depending on individual i, varying around a population mean . The term C0e–rt becomes
where β = is a fixed effect and bi = is a random effect.
Random effects are useful when data falls into natural groups. In the drug elimination model, the groups are simply the individuals under study. More sophisticated models might group data by an individual's age, weight, diet, etc. Although the groups are not the focus of the study, adding random effects to a model extends the reliability of inferences beyond the specific sample of individuals.
Mixed-effects models account for both fixed and random effects. As with all regression models, their purpose is to describe a response variable as a function of the predictor variables. Mixed-effects models, however, recognize correlations within sample subgroups. In this way, they provide a compromise between ignoring data groups entirely and fitting each group with a separate model.
Mixed-Effects Model Hierarchy
Suppose data for a nonlinear regression model falls into one of m distinct groups i = 1, ..., m. To account for the groups in a model, write response j in group i as:
yij is the response, xij is a vector of predictors, φ is a vector of model parameters, and εij is the measurement or process error. The index j ranges from 1 to ni, where ni is the number of observations in group i. The function f specifies the form of the model. Often, xij is simply an observation time tij. The errors are usually assumed to be independent and identically, normally distributed, with constant variance.
Estimates of the parameters in φ describe the population, assuming those estimates are the same for all groups. If, however, the estimates vary by group, the model becomes
In a mixed-effects model, φi may be a combination of a fixed and a random effect:
The random effects bi are usually described as multivariate normally distributed, with mean zero and covariance Ψ. Estimating the fixed effects β and the covariance of the random effects Ψ provides a description of the population that does not assume the parameters φi are the same across groups. Estimating the random effects bi also gives a description of specific groups within the data.
Model parameters do not have to be identified with individual effects. In general, design matrices A and B are used to identify parameters with linear combinations of fixed and random effects:
If the design matrices differ among groups, the model becomes
If the design matrices also differ among observations, the model becomes
Some of the group-specific predictors in xij may not change with observation j. Calling those vi, the model becomes
Specifying Mixed-Effects Models
Suppose data for a nonlinear regression model falls into one of m distinct groups i = 1, ..., m. (Specifically, suppose that the groups are not nested.) To specify a general nonlinear mixed-effects model for this data:
Define group-specific model parameters φi as linear combinations of fixed effects β and random effects bi.
Define response values yi as a nonlinear function f of the parameters and group-specific predictor variables Xi.
The model is:
This formulation of the nonlinear mixed-effects model uses the following notation:
| φi | A vector of group-specific model parameters |
| β | A vector of fixed effects, modeling population parameters |
| bi | A vector of multivariate normally distributed group-specific random effects |
| Ai | A group-specific design matrix for combining fixed effects |
| Bi | A group-specific design matrix for combining random effects |
| Xi | A data matrix of group-specific predictor values |
| yi | A data vector of group-specific response values |
| f | A general, real-valued function of φi and Xi |
| εi | A vector of group-specific errors, assumed to be independent, identically, normally distributed, and independent of bi |
| Ψ | A covariance matrix for the random effects |
| σ2 | The error variance, assumed to be constant across observations |
For example, consider a model of the elimination of a drug from the bloodstream. The model incorporates two overlapping phases:
An initial phase p during which drug concentrations reach equilibrium with surrounding tissues
A second phase q during which the drug is eliminated from the bloodstream
For data on multiple individuals i, the model is
where yij is the observed concentration in individual i at time tij. The model allows for different sampling times and different numbers of observations for different individuals.
The elimination rates rpi and rqi must be positive to be physically meaningful. Enforce this by introducing the log rates Rpi = log(rpi) and Rqi = log(rqi) and reparameterizing the model:
Choosing which parameters to model with random effects is an important consideration when building a mixed-effects model. One technique is to add random effects to all parameters, and use estimates of their variances to determine their significance in the model. An alternative is to fit the model separately to each group, without random effects, and look at the variation of the parameter estimates. If an estimate varies widely across groups, or if confidence intervals for each group have minimal overlap, the parameter is a good candidate for a random effect.
To introduce fixed effects β and random effects bi for all model parameters, reexpress the model as follows:
In the notation of the general model:
where ni is the number of observations of individual i. In this case, the design matrices Ai and Bi are, at least initially, 4-by-4 identity matrices. Design matrices may be altered, as necessary, to introduce weighting of individual effects, or time dependency.
Fitting the model and estimating the covariance matrix Ψ often leads to further refinements. A relatively small estimate for the variance of a random effect suggests that it can be removed from the model. Likewise, relatively small estimates for covariances among certain random effects suggests that a full covariance matrix is unnecessary. Since random effects are unobserved, Ψ must be estimated indirectly. Specifying a diagonal or block-diagonal covariance pattern for Ψ can improve convergence and efficiency of the fitting algorithm.
Statistics and Machine Learning Toolbox™ functions nlmefit and nlmefitsa fit the general nonlinear mixed-effects
model to data, estimating the fixed and random effects. The functions
also estimate the covariance matrix Ψ for
the random effects. Additional diagnostic outputs allow you to assess
tradeoffs between the number of model parameters and the goodness
of fit.
Specifying Covariate Models
If the model in Specifying Mixed-Effects Models assumes a group-dependent covariate such as weight (w) the model becomes:
Thus, the parameter φi
for any individual in the ith group is:
To specify a covariate model, use the
'FEGroupDesign' name-value argument of nlmefit or nlmefitsa.
'FEGroupDesign' is a p-by-q-by-m array
specifying a different p-by-q fixed-effects design
matrix for each of the m groups. Using the previous
example, the array resembles the following:
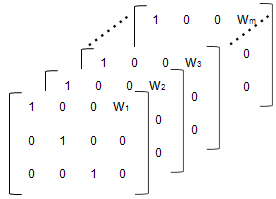
% Number of parameters in the model (Phi) num_params = 3; % Number of covariates num_cov = 1; % Assuming number of groups in the data set is 7 num_groups = 7; % Array of covariate values covariates = [75; 52; 66; 55; 70; 58; 62 ]; A = repmat(eye(num_params, num_params+num_cov),... [1,1,num_groups]); A(1,num_params+1,1:num_groups) = covariates(:,1)
Specify 'FEGroupDesign',A to use the design matrix
A.
Choosing nlmefit or nlmefitsa
Statistics and Machine Learning Toolbox provides two functions, nlmefit and nlmefitsa for fitting nonlinear mixed-effects models. Each function
provides different capabilities, which may help you decide which to use.
Approximation Methods
nlmefit provides the following
four approximation methods for fitting nonlinear mixed-effects models:
'LME'— Use the likelihood for the linear mixed-effects model at the current conditional estimates ofbetaandB. This is the default.'RELME'— Use the restricted likelihood for the linear mixed-effects model at the current conditional estimates ofbetaandB.'FO'— First-order Laplacian approximation without random effects.'FOCE'— First-order Laplacian approximation at the conditional estimates ofB.
nlmefitsa provides an additional
approximation method, Stochastic Approximation Expectation-Maximization (SAEM)
[1] with three steps :
Simulation: Generate simulated values of the random effects b from the posterior density p(b|Σ) given the current parameter estimates.
Stochastic approximation: Update the expected value of the log likelihood function by taking its value from the previous step, and moving part way toward the average value of the log likelihood calculated from the simulated random effects.
Maximization step: Choose new parameter estimates to maximize the log likelihood function given the simulated values of the random effects.
Both nlmefit and nlmefitsa
attempt to find parameter estimates to maximize a likelihood function, which is
difficult to compute. nlmefit deals with the problem by
approximating the likelihood function in various ways, and maximizing the
approximate function. It uses traditional optimization techniques that depend on
things like convergence criteria and iteration limits.
nlmefitsa, on the other hand, simulates random values of
the parameters in such a way that in the long run they converge to the values
that maximize the exact likelihood function. The results are random, and
traditional convergence tests don't apply. Therefore
nlmefitsa provides options to plot the results as the
simulation progresses, and to restart the simulation multiple times. You can use
these features to judge whether the results have converged to the accuracy you
desire.
Parameters Specific to nlmefitsa
The following parameters are specific to nlmefitsa. Most control the
stochastic algorithm.
Cov0— Initial value for the covariance matrixPSI. Must be an r-by-r positive definite matrix. If empty, the default value depends on the values ofBETA0.ComputeStdErrors—trueto compute standard errors for the coefficient estimates and store them in the outputSTATSstructure, orfalse(default) to omit this computation.LogLikMethod— Specifies the method for approximating the log likelihood.NBurnIn— Number of initial burn-in iterations during which the parameter estimates are not recomputed. Default is 5.NIterations— Controls how many iterations are performed for each of three phases of the algorithm.NMCMCIterations— Number of Markov Chain Monte Carlo (MCMC) iterations.
Model and Data Requirements
There are some differences in the capabilities of nlmefit
and nlmefitsa. Therefore some data and models are usable with
either function, but some may require you to choose just one of them.
Error models —
nlmefitsasupports a variety of error models. For example, the standard deviation of the response can be constant, proportional to the function value, or a combination of the two.nlmefitfits models under the assumption that the standard deviation of the response is constant. One of the error models,'exponential', specifies that the log of the response has a constant standard deviation. You can fit such models usingnlmefitby providing the log response as input, and by rewriting the model function to produce the log of the nonlinear function value.Random effects — Both functions fit data to a nonlinear function with parameters, and the parameters may be simple scalar values or linear functions of covariates.
nlmefitallows any coefficients of the linear functions to have both fixed and random effects.nlmefitsasupports random effects only for the constant (intercept) coefficient of the linear functions, but not for slope coefficients. So in the example in Specifying Covariate Models,nlmefitsacan treat only the first three beta values as random effects.Model form —
nlmefitsupports a very general model specification, with few restrictions on the design matrices that relate the fixed coefficients and the random effects to the model parameters.nlmefitsais more restrictive:The fixed effect design must be constant in every group (for every individual), so an observation-dependent design is not supported.
The random effect design must be constant for the entire data set, so neither an observation-dependent design nor a group-dependent design is supported.
As mentioned under Random Effects, the random effect design must not specify random effects for slope coefficients. This implies that the design must consist of zeros and ones.
The random effect design must not use the same random effect for multiple coefficients, and cannot use more than one random effect for any single coefficient.
The fixed effect design must not use the same coefficient for multiple parameters. This implies that it can have at most one nonzero value in each column.
If you want to use
nlmefitsafor data in which the covariate effects are random, include the covariates directly in the nonlinear model expression. Don't include the covariates in the fixed or random effect design matrices.Convergence — As described in the Model form,
nlmefitandnlmefitsahave different approaches to measuring convergence.nlmefituses traditional optimization measures, andnlmefitsaprovides diagnostics to help you judge the convergence of a random simulation.
In practice, nlmefitsa tends to be more
robust, and less likely to fail on difficult problems. However,
nlmefit may converge faster on problems where it
converges at all. Some problems may benefit from a combined strategy, for
example by running nlmefitsa for a while to get reasonable
parameter estimates, and using those as a starting point for additional
iterations using nlmefit.
Using Output Functions with Mixed-Effects Models
The Outputfcn field of the options structure
specifies one or more functions that the solver calls after each iteration.
Typically, you might use an output function to plot points at each
iteration or to display optimization quantities from the algorithm.
To set up an output function:
Write the output function as a MATLAB® file function or local function.
Use
statsetto set the value ofOutputfcnto be a function handle, that is, the name of the function preceded by the@sign. For example, if the output function isoutfun.m, the commandoptions = statset('OutputFcn', @outfun);specifies
OutputFcnto be the handle tooutfun. To specify multiple output functions, use the syntax:options = statset('OutputFcn',{@outfun, @outfun2});Call the optimization function with
optionsas an input argument.
For an example of an output function, see Sample Output Function.
Structure of the Output Function
The function definition line of the output function has the following form:
stop = outfun(beta,status,state)
beta is the current fixed effects.
status is a structure containing data from the current iteration. Fields in status describes the structure in detail.
state is the current state of the algorithm. States of the Algorithm lists the possible values.
stop is a flag that is
trueorfalsedepending on whether the optimization routine should quit or continue. See Stop Flag for more information.
The solver passes the values of the input arguments
to outfun at each iteration.
Fields in status
The following table lists the fields of the status structure:
| Field | Description |
|---|---|
procedure |
|
iteration | An integer starting from 0. |
inner |
A structure describing the status of the inner iterations
within the
|
fval | The current log likelihood |
Psi | The current random-effects covariance matrix |
theta | The current parameterization of Psi |
mse | The current error variance |
States of the Algorithm
The following table lists the possible values for state:
| state | Description |
|---|---|
| The algorithm is in the initial state before the first iteration. |
| The algorithm is at the end of an iteration. |
| The algorithm is in the final state after the last iteration. |
The following code illustrates how the output function might
use the value of state to decide which tasks to
perform at the current iteration:
switch state
case 'iter'
% Make updates to plot or guis as needed
case 'init'
% Setup for plots or guis
case 'done'
% Cleanup of plots, guis, or final plot
otherwise
endStop Flag
The output argument stop is a flag that is true or false.
The flag tells the solver whether it should quit or continue. The
following examples show typical ways to use the stop flag.
Stopping an Optimization Based on Intermediate
Results. The output function can stop the estimation at any iteration
based on the values of arguments passed into it. For example, the
following code sets stop to true based on the value of the log likelihood
stored in the 'fval'field of the status structure:
stop = outfun(beta,status,state)
stop = false;
% Check if loglikelihood is more than 132.
if status.fval > -132
stop = true;
endStopping an Iteration Based on GUI
Input. If you design a GUI to perform nlmefit iterations, you
can make the output function stop when a user clicks a
Stop button on the GUI. For example, the
following code implements a dialog box to cancel calculations:
function retval = stop_outfcn(beta,str,status)
persistent h stop;
if isequal(str.inner.state,'none')
switch(status)
case 'init'
% Initialize dialog
stop = false;
h = msgbox('Press STOP to cancel calculations.',...
'NLMEFIT: Iteration 0 ');
button = findobj(h,'type','uicontrol');
set(button,'String','STOP','Callback',@stopper)
pos = get(h,'Position');
pos(3) = 1.1 * pos(3);
set(h,'Position',pos)
drawnow
case 'iter'
% Display iteration number in the dialog title
set(h,'Name',sprintf('NLMEFIT: Iteration %d',...
str.iteration))
drawnow;
case 'done'
% Delete dialog
delete(h);
end
end
if stop
% Stop if the dialog button has been pressed
delete(h)
end
retval = stop;
function stopper(varargin)
% Set flag to stop when button is pressed
stop = true;
disp('Calculation stopped.')
end
end
Sample Output Function
nmlefitoutputfcn is the sample Statistics and Machine Learning Toolbox output
function for nlmefit and nlmefitsa.
It initializes or updates a plot with the fixed-effects (BETA)
and variance of the random effects (diag(STATUS.Psi)).
For nlmefit, the plot also includes the log-likelihood
(STATUS.fval).
nlmefitoutputfcn is the default output function
for nlmefitsa. To use it with nlmefit,
specify a function handle for it in the options structure:
opt = statset('OutputFcn', @nlmefitoutputfcn, …)
beta = nlmefit(…, 'Options', opt, …)nlmefitsa from using of this function,
specify an empty value for the output function:opt = statset('OutputFcn', [], …)
beta = nlmefitsa(…, 'Options', opt, …)nlmefitoutputfcn stops nlmefit or nlmefitsa if
you close the figure that it produces.See Also
Topics
References
[1] Delyon, B., M. Lavielle, and E. Moulines, Convergence of a stochastic approximation version of the EM algorithm, Annals of Statistics, 27, 94-128, 1999.