PMSM (Six-Phase)
Six-phase permanent magnet synchronous motor with sinusoidal flux distribution
Libraries:
Simscape /
Electrical /
Electromechanical /
Permanent Magnet
Description
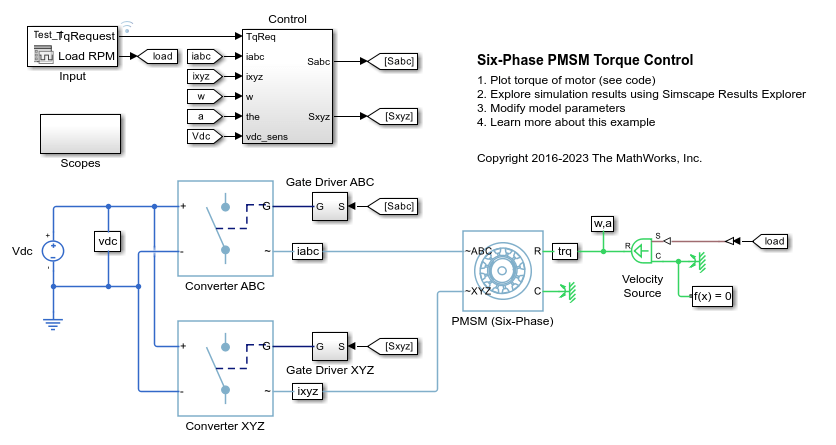
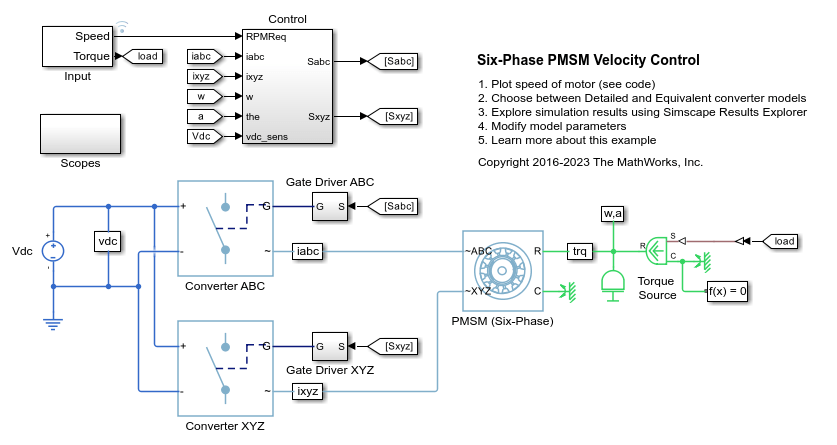
The PMSM (Six-Phase) block models a permanent magnet synchronous machine (PMSM) with a six-phase star-wound stator. Use this block to model these types of motor if the motor has six stator windings: an interior permanent magnet synchronous machine (IPMSM), surface permanent magnet synchronous machine (SPMSM), axial flux (pancake) motor, or PMSM servomotor.
A six-phase PMSM has two groups of three-phase stator windings: the ABC group and the XYZ group. These two groups have a 30 degree phase shift.
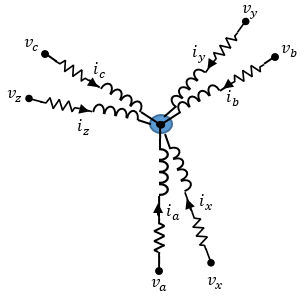
The figure shows the equivalent electrical circuit for the stator windings.
Equations
The voltages across the stator windings are
where:
va, vb, and vc are the individual phase voltages from port ~ABC to neutral port n1.
vx, vy, and vz are the individual phase voltages from port ~XYZ to neutral port n2.
Rs is the equivalent resistance of each stator winding.
ia, ib, and ic are the currents flowing from port ~ABC to port n1.
ix, iy, and iz are the currents flowing from port ~XYZ to port n2.
and are the rates of change for the magnetic flux in each stator winding.
The permanent magnet and the six windings contribute to the total flux linking each winding. The total flux is
where:
ψa, ψb, ψc, ψx, ψy, and ψz are the total fluxes that link each stator winding.
Laa, Lbb, Lcc, Lxx, Lyy, and Lzz are the self-inductances of the stator windings. These self-inductances are a function of the rotor electrical angle, θe, and depend on the stator per-phase self-inductance, Ls, and the stator inductance fluctuation, Lm.
where θr is the rotor mechanical angle.
rotor offset is
0if you define the rotor electrical angle with respect to the d-axis, or-pi/2if you define the rotor electrical angle with respect to the q-axis.Ls is the stator per-phase self-inductance. This value is the average self-inductance of each of the stator windings.
Lm is the stator inductance fluctuation. This value is the amount the self-inductance and mutual inductance fluctuate with the changing of the rotor angle.
Lab, Lac, Lba, and so on, are the mutual inductances of the stator windings. These mutual inductances are a function of the rotor electrical angle, θe, and depend on the stator mutual inductance, Ms, and the stator per-phase self-inductance, Ls.
Ms is the stator mutual inductance. This value is the average mutual inductance between the stator windings.
ψam, ψbm, ψcm, ψxm, ψym, and ψzm are the permanent magnet fluxes linking the stator windings.
The permanent magnet flux linking winding a-a' is at maximum when θe = 0° and zero when θe = 90°. Therefore, the linked motor flux is defined by:
where ψm is the permanent magnet flux linkage.
Simplified Electrical Equations
Applying a decoupled transformation to the block electrical equations produces an expression for torque that is independent of the rotor angle.
The decoupled transformation is defined by:
The transformation matrix, P, has this pseudo-orthogonal property:
Using the decoupled transformation on the stator winding voltages and currents transforms them to the dq0 frame, which is independent of the rotor angle.
To obtain the d-axis, q-axis, and zero-sequence stator voltages and flux linkages for the ABC and XYZ groups, apply the transformation to the voltage and flux linkage equations:
where:
vd, vq, vz1, vz2, v01, and v02 are the d, q, z1, and z2 components and zero-sequence stator voltages for the ABC and XYZ groups, defined by:
id, iq, iz1, iz2, i01, and i02 are the d-axis, q-axis, and zero-sequence stator currents for the ABC and XYZ groups, defined by:
is the stator d-axis inductance.
is the stator q-axis inductance.
is the stator zero-sequence inductance.
ω is the rotor mechanical rotational speed.
N is the number of rotor permanent magnet pole pairs.
The torque equation is defined by:
Model Thermal Effects
You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block contains expanded electrical conserving ports associated with the stator windings, but does not contain thermal ports.Show thermal port— The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Ports
Conserving
Parameters
References
[1] Krause, Paul, Oleg Wasynczuk, Scott Sudhoff, and Steven Pekarek, eds. Analysis of electric machinery and drive systems. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2013. https://doi.org/10.1002/9781118524336.
[2] Su, Jian Yong, Jin Bo Yang, and Gui Jie Yang. Research on Vector Control and PWM Technique of Six-Phase PMSM. Advanced Materials Research 516–517 (May 2012): 1626–31. https://doi.org/10.4028/www.scientific.net/AMR.516-517.1626.
Extended Capabilities
Version History
Introduced in R2020b