Park to Clarke Angle Transform

dq0에서 αβ0으로의 변환 구현

• 

×

라이브러리:
Simscape / Electrical / Control / Mathematical Transforms

설명

Park to Clarke Angle Transform 블록은 회전자 기준 프레임에서의 직접 성분, 직교 성분, 제로 성분을 고정자 기준 프레임에서의 alpha 성분, beta 성분, 제로 성분으로 변환합니다. 평형 시스템에서 제로 성분은 0입니다.

3상 시스템의 a상 축을 시간 t = 0에서 회전자 기준 프레임의 q축 또는 d축에 정렬되도록 블록을 구성할 수 있습니다. 아래 그림은 3상 시스템, 고정자 αβ0 기준 프레임, 회전자 dq0 기준 프레임에서 고정자 권선의 자기적 축의 방향을 보여줍니다.

• a축과 q축은 초기에 정렬됩니다.

  

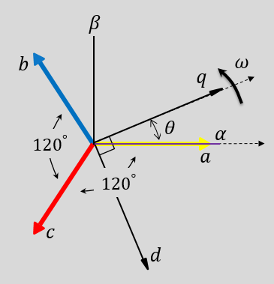
• a축과 d축은 초기에 정렬됩니다.

  

두 경우 모두 각도 θ = ωt입니다. 여기서 각각은 다음과 같습니다.

• θ는 q축 정렬의 경우 a축과 q축 사이의 각도이거나 d축 정렬의 경우 a축과 d축 사이의 각도입니다.

• ω는 d-q 기준 프레임의 회전 속도입니다.

• t는 초기 정렬에서의 시간(단위: 초)입니다.

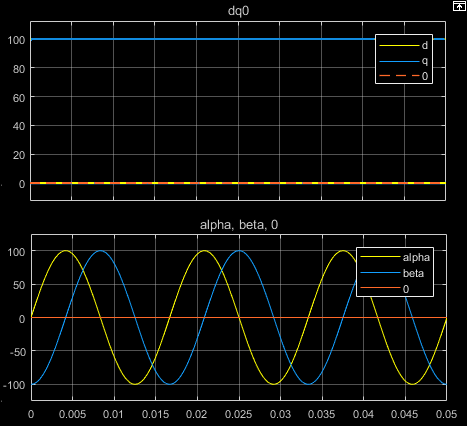
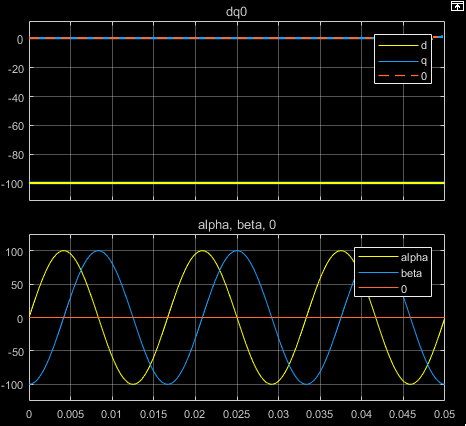
아래 그림은 등가인 평형 dq0과 αβ0의 개별 성분의 시간 응답을 보여줍니다.

• a상 벡터를 q축에 정렬

  

• a상 벡터를 d축에 정렬

  

방정식

Park to Clarke Angle Transform 블록은 a상에서 q축으로의 정렬을 위한 변환을 다음과 같이 구현합니다.

$\left[\begin{array}{c}\alpha \\ \beta \\ 0\end{array}\right]=\left[\begin{array}{ccc}\text{sin}(\theta )& \text{cos}(\theta )& 0\\ -\text{cos}(\theta )& \text{sin}(\theta )& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}d\\ q\\ 0\end{array}\right]$

여기서 각각은 다음과 같습니다.

• d와 q는 회전자 기준 프레임에서의 2상 시스템의 직접 축 성분과 직교 축 성분입니다.

• 0은 제로-시퀀스 성분입니다.

• α와 β는 고정자 기준 프레임에서의 2상 시스템의 alpha 축 성분과 beta 축 성분입니다.

a상에서 d축으로의 정렬의 경우, 블록은 다음 방정식을 사용하여 변환을 구현합니다.

$\left[\begin{array}{c}\alpha \\ \beta \\ 0\end{array}\right]=\left[\begin{array}{ccc}\text{cos}(\theta )& -\text{sin}(\theta )& 0\\ \text{sin}(\theta )& \text{cos}(\theta )& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}d\\ q\\ 0\end{array}\right]$

포트

입력

dq0 — d-q축과 제로-시퀀스 성분

벡터

회전자 기준 프레임에서의 시스템의 직접 축 성분 및 직교 축 성분과 제로-시퀀스 성분입니다.

데이터형: single | double

θ_abc — 회전 각도

스칼라 | 라디안

회전자 기준 프레임의 각위치입니다. 이 파라미터의 값은 abc 기준 프레임에서의 a상 벡터에서 dq0 기준 프레임의 초기 정렬된 축까지의 극좌표 거리와 같습니다.

데이터형: single | double

출력

αβ0 — α-β축과 제로-시퀀스 성분

벡터

고정자 기준 프레임에서의 2상 시스템의 alpha 축 성분 α, beta 축 성분 β, 제로 성분입니다.

데이터형: single | double

파라미터

a상 축 정렬 — dq0 기준 프레임 정렬

Q축 (디폴트 값) | D축

abc 기준 프레임의 a상 벡터를 회전자 기준 프레임의 d축 또는 q축에 정렬합니다.

참고 문헌

[1] Krause, P., O. Wasynczuk, S. D. Sudhoff, and S. Pekarek. Analysis of Electric Machinery and Drive Systems. Piscatawy, NJ: Wiley-IEEE Press, 2013.

확장 기능

C/C++ 코드 생성
Simulink® Coder™를 사용하여 C 코드나 C++ 코드를 생성할 수 있습니다.

버전 내역

R2017b에 개발됨

참고 항목

블록

• Clarke Transform | Clarke to Park Angle Transform | Inverse Clarke Transform | Inverse Park Transform | Park Transform