Cross-Correlation of Two Exponential Sequences
Compute and plot the cross-correlation of two 16-sample exponential sequences, and , with .
N = 16; n = 0:N-1; a = 0.84; b = 0.92; xa = a.^n; xb = b.^n; r = xcorr(xa,xb); stem(-(N-1):(N-1),r)

Determine analytically to check the correctness of the result. Use a larger sample rate to simulate a continuous situation. The cross-correlation function of the sequences and for , with , is
fs = 10;
nn = -(N-1):1/fs:(N-1);
cn = (1 - (a*b).^(N-abs(nn)))/(1 - a*b) .* ...
(a.^nn.*(nn>0) + (nn==0) + b.^-(nn).*(nn<0));Plot the sequences on the same figure.
hold on plot(nn,cn) xlabel('Lag') legend('xcorr','Analytic')
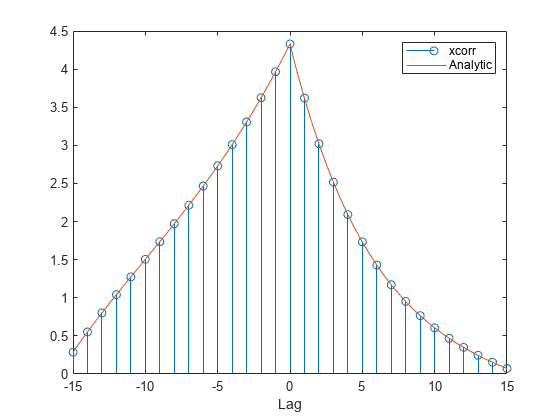
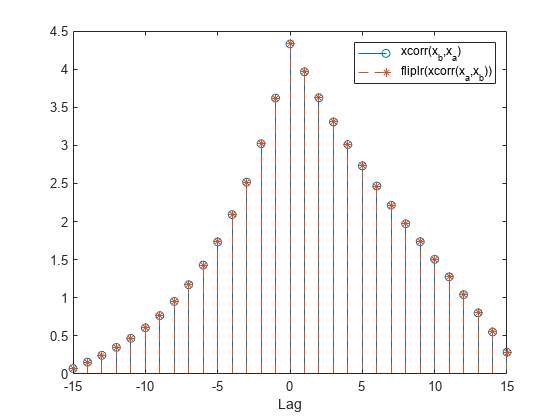
Verify that switching the order of the operands reverses the sequence.
figure stem(-(N-1):(N-1),xcorr(xb,xa)) hold on stem(-(N-1):(N-1),fliplr(r),'--*') xlabel('Lag') legend('xcorr(x_b,x_a)','fliplr(xcorr(x_a,x_b))')
Generate the 20-sample exponential sequence . Compute and plot its cross-correlations with and . Output the lags to make the plotting easier. xcorr appends zeros at the end of the shorter sequence to match the length of the longer one.
xc = 0.77.^(0:20-1);
[xca,la] = xcorr(xa,xc);
[xcb,lb] = xcorr(xb,xc);
figure
subplot(2,1,1)
stem(la,xca)
subplot(2,1,2)
stem(lb,xcb)
xlabel('Lag')