Tire (Magic Formula)

Tire defined by Magic Formula coefficients

• 

Libraries:
Simscape / Driveline / Tires & Vehicles

Description

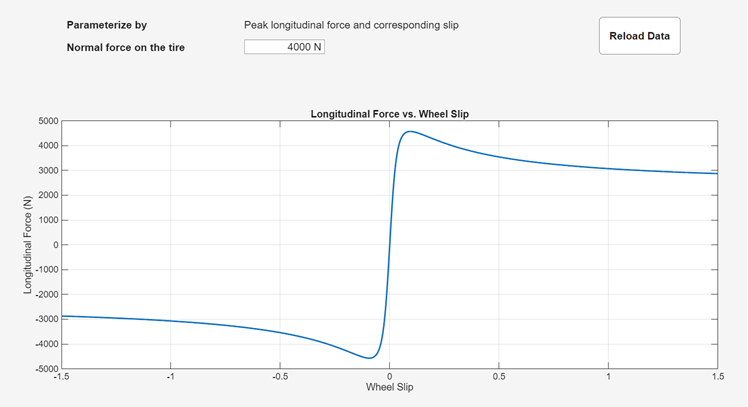
The Tire (Magic Formula) block represents a tire with longitudinal behavior given by the Magic Formula [1], an empirical equation based on four fitting coefficients. You can model tire dynamics under constant or variable pavement conditions.

The longitudinal direction of the tire is the same as its direction of motion as it rolls on pavement. This block is a structural component based on the Tire-Road Interaction (Magic Formula) block.

To increase the fidelity of the tire model, you can specify properties such as compliance, inertia, rolling resistance, and varying effective rolling radius. However, these properties increase the complexity of the tire model and can slow down simulation. Consider neglecting tire compliance and inertia if simulating the model in real time or if preparing the model for hardware-in-the-loop (HIL) simulation.

Tire Model

The block treats the tire as a rigid wheel-tire combination that is in contact with the road and subject to slip. When torque drives the wheel axle, the tire transmits longitudinal force, F_x, to the road. The tire transfers the resulting reaction as a force back on the wheel. This action rotates the wheel to generate longitudinal motion. If you model tire compliance, the tire also flexibly deforms under load. If you set the Effective rolling radius model to Load and velocity dependent (Magic Formula), the tire radius also changes depending on the load and rotational velocity.

The figure shows the forces acting on the tire. The table defines the tire model variables.

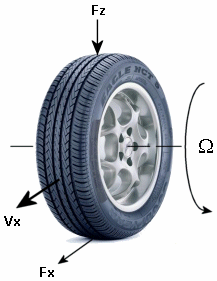
Tire Model Variables

Symbol	Description
rw	Tire rolling radius.
Vx	Wheel hub longitudinal velocity.
u	Tire longitudinal deformation.
Ω	Wheel angular velocity.
$${\Omega }^{\prime }=\Omega +\frac{\dot{u}}{r_W}$$	Contact point angular velocity. If there is no tire longitudinal deformation, $$u=0$$.
$$V_T=r_w{\Omega }^{\prime }=r_w\Omega +\dot{u}$$	Tire tread longitudinal velocity. Typically, the tire tread longitudinal velocity has a component due to tire rotation, rwΩ, and an optional component due to tire deformation, $$\dot{u}$$.
$$V_{sx}=V_x-V_T$$	Contact patch slip velocity. If there is no tire longitudinal compliance, $$u=0$$.
$$k=-\frac{V_{sx}}{{\left|V_x\right|}_{smooth}}$$	Wheel slip for a tire without compliance.
Vth	Wheel hub threshold velocity.
VXLOW	Lower boundary of slip denominator.
Fz	Vertical load on tire.
Fx	Longitudinal force exerted on the tire at the contact point.
$$C_{F_x}={\left(\frac{\partial F_x}{\partial u}\right)}_0$$	Tire longitudinal stiffness under deformation.
$$b_{F_x}={\left(\frac{\partial F_x}{\partial \dot{u}}\right)}_0$$	Tire longitudinal damping under deformation.
Iw	Wheel-tire inertia, such that the effective mass is equal to $$\frac{I_w}{r_w^2}$$
τdrive	Torque applied by the axle to the wheel.

Tire Kinematics and Response

You can model roll, slip, and deformation.

Roll and Slip

The equation for translational motion of a non-slipping, non-compliant tire is $$V_x=r_w\Omega$$. When tires experience slip, they develop a longitudinal force, F_x.

The contact patch slip velocity is $$V_{sx}=V_x-r_w\Omega -\dot{u}$$. For a tire without compliance, u = 0. The unsmoothed contact patch slip is

$$k=-\frac{V_{sx}}{\left|V_x\right|},$$

and the block saturates the slip denominator as

$$\left|V_x\right|=\{\begin{array}{ll}{V}_{XLOW}\hfill & \text{if }\left|V_x\right|<V_{XLOW}\hfill \\ \left|V_x\right|\hfill & \text{otherwise}\hfill \end{array}$$

where V_XLOW is the Lower boundary of slip denominator, VXLOW parameter. The block smoothly transitions |V_x| to V_XLOW over the transition regions -V_XLOW - V_th/2 < V_x < -V_XLOW + V_th/2 and V_XLOW - V_th/2 < V_x < V_XLOW + V_th/2. The block saturates slip according to

$$k=\{\begin{array}{ll}kpumin\hfill & \text{if }-\frac{V_{sx}}{\left|V_x\right|}<kpumin\hfill \\ kpumax\hfill & \text{if }-\frac{V_{sx}}{\left|V_x\right|}>kpumax\hfill \\ -\frac{V_{sx}}{\left|V_x\right|}\hfill & \text{otherwise}\hfill \end{array}$$

where kpumin is the Minimum valid wheel slip, KPUMIN parameter and kpumax is the Maximum valid wheel slip, KPUMAX parameter. The block transitions k over the regions kpumin - k_th/2 < k < kpumin + k_th/2 and kpumax - k_th/2 < k < kpumax + k_th/2. The block defines the slip smoothing threshold as

$$k_{th}=\frac{V_{th}}{1m/s}.$$

For this equation, a locked, sliding wheel has k = -1. For perfect rolling, k = 0.

Deformation

When you set Compliance to Specify stiffness and damping, the block treats the tire as flexible. When the tire deforms, the tire-road contact point turns at a slightly different angular velocity, Ω′, from the wheel velocity, Ω, which generates contact patch slip. The block defines the deforming tire as a translational spring-damper of stiffness, C_Fx, and damping, b_Fx.

When you set Compliance to No compliance - Suitable for HIL simulation, $$u=0$$, and there is no tire longitudinal deformation at any time in the simulation, such that $${\Omega }^{\prime }=\Omega$$.

Tire and Wheel Dynamics

The block is equivalent to this component diagram. The block simulates both transient and steady-state behavior and represents starting and stopping. The Translational Spring and Translational Damper blocks are equivalent to the tire stiffness C_Fx and damping b_Fx, respectively. The Tire-Road Interaction (Magic Formula) block represents the longitudinal force F_x on the tire as a function of F_z, and k using the Magic Formula, where k is the independent slip variable and F_z is the input signal at port N.

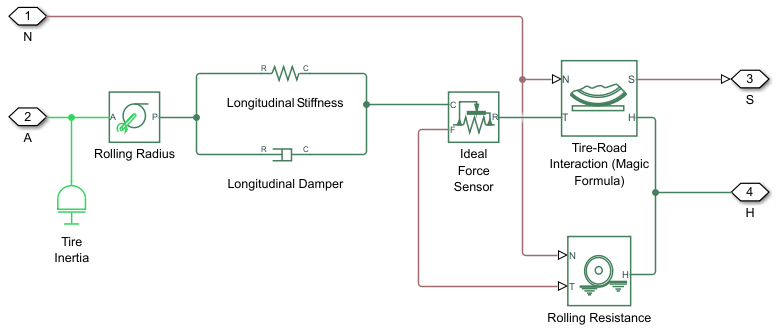
The block labeled Rolling Radius is the tire rolling radius r_w. The inertia value is the effective inertia, $$\frac{I_w}{r_w^2}$$. The tire characteristic function f(k′, F_z) determines the longitudinal force F_x. Together with the driveshaft torque applied to the wheel axis, F_x determines the wheel angular motion and longitudinal motion.

When you do not model tire compliance, the block omits the Longitudinal Stiffness and Longitudinal Damper blocks in the diagram, and contact variables revert to wheel variables. In this case, the tire effectively has infinite stiffness, and port P of Rolling Radius connects directly to port C of Ideal Force Sensor block.

When you set Rolling Resistance to a setting other than Pressure and velocity dependent (Magic Formula), the block omits the Ideal Force Sensor block and connection T of the Rolling Resistance block. When you set Compliance to No compliance - Suitable for HIL simulation, Port P of the Rolling Radius connects directly to the Ideal force sensor port C or port T of the Tire-Road Interaction (Magic Formula) block.

Effective Rolling Radius

The block determines an effective rolling radius to account for centrifugal growth and reduction due to loading such that

$$\begin{array}{l}{r}_w=R_{\Omega }-\frac{F_{z0}}{c_z}\left(D_{reff}\arctan \left(B_{reff}\frac{F_z}{F_{z0}}\right)+F_{reff}\frac{F_z}{F_{z0}}\right)\\ R_{\Omega }=R_0\left(q_{re0}+q_{v1}{\left(\frac{\Omega R_0}{V_0}\right)}^2\right)\end{array}$$

where:

• r_w is the effective rolling radius.

• R_Ω is the centrifugal growth of the free tire radius.

• F_z is the vertical load on the tire.

• F_z0 is the Tire nominal vertical load, FNOMIN parameter.

• c_z is the Vertical stiffness parameter.

• Ω is the wheel rotational velocity.

The quantities F_z and Ω vary with time.

These quantities correspond to TIR file values and block parameters:

Variable	TIR File Identifier	Parameter Name
Breff	BREFF	Low load stiffness effective rolling radius, BREFF
Dreff	DREFF	Peak value of effective rolling radius, DREFF
Freff	FREFF	High load stiffness effective rolling radius, FREFF
qre0	Q_RE0	Ratio of nominal tire radius with non-rolling free tire radius, Q_RE0
qv1	Q_V1	Tire radius increase with speed, Q_V1

Note

If your TIR file does not provide Q_RE0 and Q_V1, set these values to 1 and 0, respectively. The sdlUtility.tirread function handles this automatically.

Assumptions and Limitations

• The block assumes only longitudinal motion and includes no camber, turning, or lateral motion.

• Tire compliance implies a time lag in the response of the tire to the forces on it. Time lag simulation increases model fidelity but reduces simulation performance. See Adjust Model Fidelity.

Examples

Limited Slip Differential with Clutches

A comparison between the behavior of an open differential and a limited slip differential with clutch packs. The limited slip differential is modeled using components from the Gears library and Clutches library in Simscape™ Driveline™. Wheel slip is limited by clutches that engage when the torque applied to the input of the differential exceeds a threshold. The clutches lock the differential so that the output shafts of the differential spin at the same speed.

Open Model

Tire Parameterization and Performance

Use Simscape™ Driveline™ to fit tire Magic Formula coefficients to experimental data and to measure the simulated stopping distance of a vehicle supported by the tires. The example uses the sdlUtility.tirread function to load initial tire parameters from a .TIR file. Then, the example uses the MATLAB® optimization function fminsearch with a test harness model to fit the tire coefficients to the experimental data. Other products available for performing this type of parameter fitting with Simscape Driveline models are the Optimization Toolbox™ and Simulink® Design Optimization™. These products provide predefined functions to manipulate and analyze blocks using GUIs or a command line approach. This example uses Fast Restart to quickly simulate tire response for different parameters during the optimization.

Open Model

Torsen Differential

A comparison between the behavior of an open differential and a Torsen limited slip differential. The Torsen differential is modeled using components from the Gears library in Simscape™ Driveline™. Slip is limited in the Torsen differential because it uses non-backdrivable worm gears, which are modeled by Sun-Planet Worm Gear components. The result is higher torque applied to the wheel with greater traction, and identical speeds for the left and right axles.

Open Model

Vehicle with Dual Clutch Transmission

A vehicle with a five-speed dual-clutch transmission. Gear shifts are implemented via the two clutches, one clutch pressure being ramped up as the other clutch pressure is ramped down. Gear pre-selection via dog clutches ensures that the correct gear is fully selected before the on-going clutch is enabled.

Open Model

Vehicle with Four-Speed Transmission

A complete vehicle with Simscape™ Driveline™ components, including the engine, drivetrain, four-speed transmission, tires, and longitudinal vehicle dynamics. The transmission controller is implemented as a state machine in Stateflow®, selecting the gear based on throttle and vehicle speed.

Open Model

Vehicle with Four-Wheel Drive

A four-wheel drive vehicle starting from rest and ascending a 15 degree incline. Initially the vehicle rolls backwards until the engine develops sufficient torque to counter the slope. The tire compliance dynamics can be seen as the vehicle starts to accelerate. The model variant chosen for all of the tires can be set to the Simple, Friction Parameterized, or Magic Formula tire model using the hyperlinks in the model.

Open Model

Ports

Input

N — Normal force, N

physical signal

Physical signal input port associated with the normal force acting on the tire, in N. The normal force is positive if it acts downward on the tire, pressing it against the pavement.

M — Magic formula coefficients, unitless

physical signal | vector

Physical signal input port associated with the Magic Formula coefficients. Provide the Magic Formula coefficients as a four-element vector, specified in the order [B, C, D, E].

Dependencies

To enable this port, set Parameterize by to Physical signal Magic Formula coefficients.

Output

S — Slip

physical signal

Physical signal output port associated with the relative slip, k, between the tire and road.

Conserving

A — Axle

mechanical rotational

Mechanical rotational port associated with the axle that the tire sits on.

H — Hub

mechanical translational

Mechanical translational port associated with the wheel hub that transmits the thrust generated by the tire to the remainder of the vehicle.

Parameters

Main

Parameterize by — Parameterization method

Peak longitudinal force and corresponding slip (default) | Constant Magic Formula coefficients | Load-dependent Magic Formula coefficients | Physical signal Magic Formula coefficients

Magic Formula tire simulation option. Select how the block parameterizes the tire using the Magic Formula:

• Peak longitudinal force and corresponding slip — Parameterize the Magic Formula with the physical characteristics of the tire.

• Constant Magic Formula coefficients — Specify the parameters that define the constant B, C, D, and E coefficients as scalars.

• Load-dependent Magic Formula coefficients — Specify the parameters that define the load-dependent C, D, E, K, H, and V coefficients as vectors, one for each coefficient.

• Physical signal Magic Formula coefficients — Specify the Magic Formula coefficients using port M as a four-element vector in the order [B, C, D,E].

Rated vertical load — Rated load force

3000 N (default) | positive scalar

Rated vertical load force F_z0.

Dependencies

To enable this parameter, set Parameterize by to Peak longitudinal force and corresponding slip.

Peak longitudinal force at rated load — Maximum longitudinal force at rated load

3500 N (default) | positive scalar

Maximum longitudinal force F_x0 that the tire exerts on the wheel when the vertical load equals its rated value F_z0.

Dependencies

To enable this parameter, set Parameterize by to Peak longitudinal force and corresponding slip.

Slip at peak force at rated load (percent) — Percent slip at maximum longitudinal force and rated load

10 (default) | positive scalar

Contact slip, k₀, expressed as a percentage (%), when the longitudinal force equals its maximum value F_x0 and the vertical load equals its rated value F_z0.

Dependencies

To enable this parameter, set Parameterize by to Peak longitudinal force and corresponding slip.

Magic Formula B coefficient — Constant Magic Formula B coefficient

10 (default) | positive scalar

Load-independent Magic Formula B coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Magic Formula C coefficient — Constant Magic Formula C coefficient

1.9 (default) | positive scalar

Load-independent Magic Formula C coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Magic Formula D coefficient — Constant Magic Formula D coefficient

1 (default) | positive scalar

Load-independent Magic Formula D coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Magic Formula E coefficient — Constant Magic Formula E coefficient

0.97 (default) | positive scalar

Load-independent Magic Formula E coefficient.

Dependencies

To enable this parameter, set Parameterize by to Constant Magic Formula coefficients.

Tire nominal vertical load, FNOMIN — Normal force

4000 N (default) | positive scalar

Nominal normal force F_z0 on the tire.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula C-coefficient parameter, p_Cx1 — Variable Magic Formula C coefficient

1.685 (default) | scalar

Load-dependent Magic Formula C coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula D-coefficient parameters, [p_Dx1 p_Dx2] — Variable Magic Formula D coefficient

[1.21, -.037] (default) | vector

Load-dependent Magic Formula D coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula E-coefficient parameters, [p_Ex1 p_Ex2 p_Ex3 p_Ex4] — Variable Magic Formula E coefficient

[.344, .095, -.02, 0] (default) | vector

Load-dependent Magic Formula E coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula BCD-coefficient parameters, [p_Kx1 p_Kx2 p_Kx3] — Variable Magic Formula K coefficient

[21.51, -.163, .245] (default) | vector

Load-dependent Magic Formula K coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula H-coefficient parameters, [p_Hx1 p_Hx2] — Variable Magic Formula H coefficient

[-.002, .002] (default) | vector

Load-dependent Magic Formula H coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Magic Formula V-coefficient parameters, [p_Vx1 p_Vx2] — Variable Magic Formula V coefficient

[0, 0] (default) | vector

Load-dependent Magic Formula V coefficient.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients.

Geometry

Effective rolling radius model — Rolling radius model option

Constant radius (default) | Load and velocity dependent (Magic Formula)

Whether to treat the rolling radius as constant or dependent on load and velocity.

Dependencies

To enable this parameter, set Parameterize to Load-dependent Magic Formula coefficients.

Rolling radius — Loaded tire radius

0.3 m (default) | positive scalar

Loaded tire-wheel radius, r_w.

Dependencies

To enable this parameter, either set:

• Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Constant radius, or

• Parameterize by to Peak longitudinal force and corresponding slip, Constant Magic Formula coefficients, or Physical signal Magic Formula coefficients.

Non-rolling free tire radius, R0 — Non-rolling free tire radius

0.3 m (default) | positive scalar

Non-rolling free tire radius value associated with the Magic Formula. R0 is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Low load stiffness effective rolling radius, BREFF — B_reff variable

8.39 (default) | positive scalar

Effective rolling radius at low load stiffness. BREFF is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Peak value of effective rolling radius, DREFF — D_reff variable

0.26 (default) | positive scalar

Peak value of effective rolling radius. DREFF is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

High load stiffness effective rolling radius, FREFF — F_reff variable

0.074 (default) | positive scalar

Effective rolling radius at high load stiffness. FREFF is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Ratio of nominal tire radius with non-rolling free tire radius, Q_RE0 — q_re0 variable

0.99 (default) | positive scalar

Ratio of the nominal tire radius to the non-rolling free tire radius. Q_RE0 is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Tire radius increase with speed, Q_V1 — q_v1 variable

0.008 (default) | positive scalar

Tire radius increase with respect to speed. Q_V1 is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Nominal hub longitudinal speed, LONGVL — Nominal hub longitudinal speed

17 m/s (default) | positive scalar

Nominal hub longitudinal speed. LONGVL is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Vertical stiffness — Vertical stiffness

5e5 N/m (default) | positive scalar

Vertical stiffness of the tire.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and Effective rolling radius model to Load and velocity dependent (Magic Formula).

Rolling Resistance

Model rolling resistance — Rolling resistance option

off (default) | on

Whether to include rolling resistance in the tire simulation.

Resistance model — Rolling resistance option

Constant coefficient (default) | Pressure and velocity dependent SAE J2452 | Pressure and velocity dependent (Magic Formula)

Whether to include resistance using a constant coefficient or pressure and velocity dependent resistance:

• Constant coefficient — Neglect rolling resistance.

• Pressure and velocity dependent SAE J2452 — Parameterize rolling resistance in accordance with SAE J2452.

• Pressure and velocity dependent (Magic Formula) — Parameterize rolling resistance in accordance with the Magic Formula.

Dependencies

To enable this parameter, select Model rolling resistance.

Constant coefficient — Proportionality constant

0.015 (default) | positive scalar

Coefficient that sets the proportionality between the normal force and the rolling resistance force. The parameter must be greater than zero.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Constant coefficient.

Tire pressure — Tire pressure

250e3 Pa (default) | positive scalar

Inflation pressure of the tire. The parameter must be greater than zero.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Pressure and velocity dependent SAE J2452 or Pressure and velocity dependent (Magic Formula).

Alpha — Tire pressure equation exponent

-0.003 (default) | scalar

Exponent of the tire pressure in the model equation.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Pressure and velocity dependent SAE J2452.

Beta — Normal force equation exponent

0.97 (default) | scalar

Exponent of the normal force model equation.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Pressure and velocity dependent SAE J2452.

Coefficient A — Velocity-independent force component A

84e-4 (default)

Velocity-independent force component in the model equation. The parameter must be greater than zero.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Pressure and velocity dependent SAE J2452.

Coefficient B — Velocity-dependent force component B

6.2e-4 s/m (default) | positive scalar

Velocity-dependent force component in the model equation. The parameter must be greater than zero.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Pressure and velocity dependent SAE J2452.

Coefficient C — Velocity-dependent force component C

1.6e-4 s^2/m^2 (default) | positive scalar

Force component that depends on the square of the velocity term in the model equation. The parameter must be greater than zero.

Dependencies

To enable this parameter, select Model rolling resistance and set Rolling resistance to Pressure and velocity dependent SAE J2452.

Tire nominal pressure, NOMPRES — Nominal tire pressure

240e3 Pa (default) | positive scalar

Nominal tire pressure. NOMPRES it the TIR file identifier.

Dependencies

To enable this parameter, set Resistance model to Pressure and velocity dependent (Magic Formula).

Tire nominal vertical load, FNOMIN — Normal force

4000 N (default) | positive scalar

Nominal normal force, F_z0, on tire. FNOMIN is the TIR file identifier.

Dependencies

To enable this parameter, set Resistance model to Pressure and velocity dependent (Magic Formula).

Nominal hub longitudinal speed, LONGVL — Nominal hub longitudinal speed

16 m/s (default) | positive scalar

Nominal hub longitudinal speed. LONGVL is the TIR file identifier.

Dependencies

To enable this parameter, set Resistance model to Pressure and velocity dependent (Magic Formula).

Q-coefficient parameters [qsy1 qsy2 qsy3 qsy4 qsy5 qsy6 qsy7 qsy8] — Magic Formula Q-coefficients

[.0082, 0, .0014, .001, 0, 0, 1.08, -.5] 1 (default) | vector of length 8

Magic Formula Q coefficients. qsy1,…, qsy8 correspond to the TIR file identifiers.

Dependencies

To enable this parameter, set Resistance model to Pressure and velocity dependent (Magic Formula).

Velocity threshold for rolling resistance — Wheel hub velocity threshold for mathematical slip model

0.001 m/s (default) | positive scalar

Velocity at which the full rolling resistance force is transmitted to the rolling hub. The parameter ensures that the force remains continuous during velocity direction changes, which increases the numerical stability of the simulation. The parameter must be greater than zero.

Dependencies

To enable this parameter, select Model rolling resistance.

Scaling

Enable scaling coefficients — Scaling option

off (default) | on

Whether to include scaling coefficients in the Magic Formula parameterization.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients or set Resistance model to Pressure and velocity dependent (Magic Formula).

Scale factor of Fx nominal vertical load, LFZO — F_x nominal vertical load

1 (default) | positive scalar

Scale factor of the F_x nominal vertical load, λ_FZO. LFZO is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx shape factor, LCX — F_x shape factor

1 (default) | positive scalar

Scale factor of the F_x shape factor, λ_LCX. LCX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx peak friction coefficient, LMUX — F_x peak friction coefficient

1 (default) | positive scalar

Scale factor of the F_x peak friction coefficient, λ_μX. LMUX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx curvature factor, LEX — F_x curvature factor

1 (default) | positive scalar

Scale factor of the F_x curvature factor, λ_EX. LEX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx slip stiffness, LKX — F_x slip stiffness

1 (default) | positive scalar

Scale factor of the F_x slip stiffness, λ_KX. LKX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx horizontal shift, LHX — F_x horizontal shift

1 (default) | positive scalar

Scale factor of the F_x horizontal shift, λ_hX. LHX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of Fx vertical shift, LVX — F_x vertical shift

1 (default) | positive scalar

Scale factor of the F_x vertical shift, λ_VX. LVX is the TIR file identifier.

Dependencies

To enable this parameter, set Parameterize by to Load-dependent Magic Formula coefficients and select Enable scaling coefficients.

Scale factor of rolling resistance, LMY — Rolling resistance

1 (default) | positive scalar

Scale factor of the rolling resistance, λ_MY. LMY is the TIR file identifier.

Dependencies

To enable this parameter, either set

• Parameterize by to Load and velocity dependent (Magic Formula), or

• Resistance model to Pressure and velocity dependent (Magic Formula)

and select Enable scaling coefficients.

Dynamics

Compliance — Dynamical compliance option

No compliance - Suitable for HIL simulation (default) | Specify stiffness and damping

Whether to the include dynamical compliance of the tire:

• No compliance - Suitable for HIL simulation — The block neglects dynamical compliance.

• Specify stiffness and damping — The block treats the tire as a spring-damper system under load.

Longitudinal stiffness — Longitudinal stiffness

1e6 N/m (default) | positive scalar

Tire longitudinal stiffness C_Fx.

Dependencies

To enable this parameter, set Compliance to Specify stiffness and damping.

Longitudinal damping — Longitudinal damping

1000 N/(m/s) (default) | positive scalar

Tire longitudinal damping b_Fx.

Dependencies

To enable this parameter, set Compliance to Specify stiffness and damping.

Inertia — Inertia model

No inertia (default) | Specify inertia and initial velocity

Model for the rotational inertia of the tire.

• No inertia — The block neglects dynamical compliance.

• Specify inertia and initial velocity — The block treats the tire as a stiff, damped spring and deforms under load.

Tire inertia — Rotational inertia

1 kg*m^2 (default) | positive scalar

Rotational inertia I_w of the wheel-tire assembly.

Dependencies

To enable this parameter, set Inertia to Specify inertia and initial velocity.

Initial velocity — Initial rotational velocity

0 rad/s (default) | scalar

Initial angular velocity, Ω(0), of the tire.

Dependencies

To enable this parameter, set Inertia to Specify inertia and initial velocity.

Advanced

Lower boundary of slip denominator, VXLOW — Lower boundary of slip denominator

1 m/s (default) | positive scalar

Lower boundary of slip denominator, V_XLOW. VXLOW is the TIR file identifier.

Velocity threshold — Wheel hub velocity threshold for mathematical slip model

0.1 m/s (default) | positive scalar

Threshold velocity the block uses to transition between slip regimes, V_th. To learn more, see Roll and Slip.

Minimum valid wheel slip, KPUMIN — Minimum wheel slip threshold

-1.5 (default) | scalar

Minimum valid wheel slip. A negative value represents wheel slip in the reverse rotational direction.

Maximum valid wheel slip, KPUMAX — Maximum wheel slip threshold

1.5 (default) | scalar

Maximum valid wheel slip.

More About

Real-Time and Hardware-in-the-Loop Simulation

For optimal simulation performance, set the Dynamics > Compliance parameter to No compliance - Suitable for HIL simulation.

References

[1] Besselink, I. J.M., A. J.C. Schmeitz, and H. B. Pacejka. “An Improved Magic Formula/Swift Tyre Model That Can Handle Inflation Pressure Changes.” Vehicle System Dynamics 48, no. sup1 (December 2010): 337–52. https://doi.org/10.1080/00423111003748088.

[2] Pacejka, H. B. Tire and Vehicle Dynamics. Elsevier Science, 2005.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2011a

R2023a: Magic Formula compatibility enhancements

The block includes a wider set of Magic Formula parameters. You can now parameterize the block or the effective rolling radius by using load-dependent Magic Formula coefficients by using these parameter settings:

• Parameterize by to Load-dependent Magic Formula coefficients

• Effective rolling radius model to Load and velocity dependent (Magic Formula)

You can also model scaling coefficients when you select Enable scaling coefficients.

These parameters are new for all parameterizations:

• Lower boundary of slip denominator, VXLOW

• Minimum valid wheel slip, KPUMIN

• Maximum valid wheel slip, KPUMAX