엔드포인트 힘과 모멘트의 균형을 맞추기 위해 조인트 토크 계산하기

라이브 스크립트 열기

평면 로봇의 엔드 이펙터에 작용하는 엔드포인트 힘의 균형을 맞추기 위해 토크를 생성합니다. 엔드 이펙터는 엔드 이펙터의 바디 프레임에 정의하거나, 엔드 이펙터 프레임에서 일정 거리 떨어진 지점에 고정된 툴팁(tool-tip) 프레임으로 정의할 수 있습니다. 다양한 방법을 사용하여 조인트 토크를 계산하려면 rigidBodyTree 로봇 모델에 geometricJacobian 객체 함수와 inverseDynamics 객체 함수를 사용합니다.

로봇 초기화하기

twoJointRigidBodyTree 로봇은 2차원 평면 로봇입니다. 조인트 컨피규레이션은 열 벡터로 출력됩니다.

twoJointRobot = twoJointRigidBodyTree("column");

이 예제에서는 "tool" 바디의 바디 프레임에 작용하는 외력을 에뮬레이션해 보겠습니다. 이 힘은 "tool" 바디에서 일정 거리 떨어진 프레임에도 작용할 수 있습니다. 이 프레임을 "toolTip"이라고 하겠습니다. "tool" 바디 프레임에서 "[0.1,0,0]" 평행 이동 벡터를 사용하여 새 "toolTip" 프레임을 "tool" 바디에 추가합니다.

toolBody = twoJointRobot.Bodies{end};
addFrame(toolBody,"toolTip","tool",trvec2tform([0.1,0,0]));

엔드 이펙터를 "toolTip" 프레임으로 지정합니다. 드롭다운에서 엔드 이펙터를 선택하여 "tool" 바디 프레임으로 전환할 수도 있습니다. 그 이후의 계산은 프레임에 관계없이 일관적으로 유지됩니다.

eeFrameName = "toolTip"
eeFrameName = 
"toolTip"

문제 설정

엔드포인트 힘 eeForce는 엔드 이펙터 바디("tool" or "toolTip" frame)에 작용하는 선형적인 힘과 모멘트의 조합으로 이루어진 열 벡터입니다. 참고로 이 벡터는 베이스 좌표 프레임에서 표현되며, 아래와 같습니다.

endpointforcedepiction.PNG

fx = 2; 
fy = 2;
fz = 0;
nx = 0;
ny = 0;
nz = 3;
eeForce = [nx;ny;nz;fx;fy;fz];

균형 토크에 대한 로봇의 조인트 컨피규레이션을 지정합니다.

q = [pi/3;pi/4];
Tee = getTransform(twoJointRobot,q,eeFrameName);

기하 야코비 행렬 방법

가상 일(virtual work)[1] 원리를 적용하여, geometricJacobian 객체 함수를 사용하고 해당 야코비 행렬의 전치에 엔드포인트 힘 벡터를 곱해서 균형 토크를 구합니다.

J = geometricJacobian(twoJointRobot,q,eeFrameName);
jointTorques = J' * eeForce;
fprintf("Joint torques using geometric Jacobian (Nm): [%.3g, %.3g]",jointTorques);
Joint torques using geometric Jacobian (Nm): [1.16, 1.53]

공간적으로 변환된 힘에 대한 역동역학

또 다른 방법으로, 엔드포인트 힘을 베이스 프레임으로 공간적으로 변환하여 역동역학을 계산하는 방법을 사용하여 균형 토크를 구할 수 있습니다.

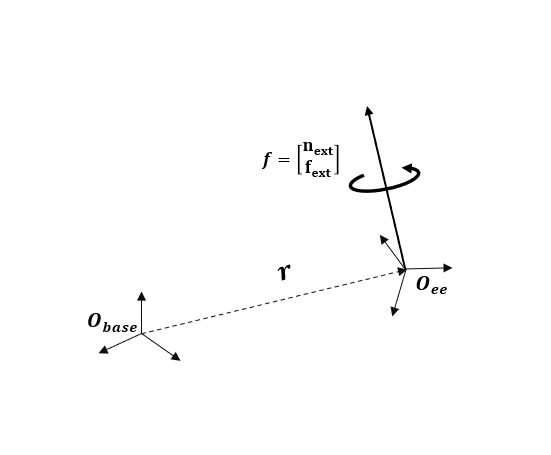
렌치를 엔드 이펙터 프레임에서 베이스 프레임으로 공간적으로 변환한다는 것은 새로운 렌치가 공간적으로 베이스 프레임과 동일한 프레임에 가해지되, 여전히 엔드 이펙터 바디에 고정된 채로 작용한다는 의미입니다. 이 새로운 렌치는 엔드 이펙터 원점에서 가해진 원래의 렌치와 동일한 효과를 가집니다. 아래 그림에서 fext와 next 는 각각 엔드포인트의 선형적 힘과 모멘트이고, feebase 와 neebase 는 엔드 이펙터("tool" 프레임 또는 "toolTip" 프레임)에서 각각 공간적으로 변환된 힘과 모멘트입니다. 아래 코드 조각에서 fbase_ee가 공간적으로 변환된 렌치입니다.

r = tform2trvec(Tee);
fbase_ee = [cross(r,[fx fy fz])' + [nx;ny;nz]; fx;fy;fz];
fext = -externalForce(twoJointRobot, eeFrameName, fbase_ee);
jointTorques2 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques2)
Joint torques using inverse dynamics (Nm): [1.16, 1.53]

엔드 이펙터 힘에 대한 역동역학

엔드포인트 힘을 베이스 프레임으로 공간적으로 변환하는 대신에 세 번째 가능한 방법은 엔드 이펙터 힘을 자체 좌표 프레임(fee_ee)으로 표현하는 것입니다. 모멘트와 선형적 힘으로 구성된 벡터를 엔드 이펙터 좌표 프레임으로 변환합니다. 그런 다음, 그 힘과 현재 컨피규레이션을 externalForce 함수에 지정합니다. 이 힘 벡터로부터 역동역학을 계산합니다.

eeLinearForce = Tee \ [fx;fy;fz;0];
eeMoment = Tee \ [nx;ny;nz;0];
fee_ee = [eeMoment(1:3); eeLinearForce(1:3)];
fext = -externalForce(twoJointRobot,eeFrameName,fee_ee,q);
jointTorques3 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques3);
Joint torques using inverse dynamics (Nm): [1.16, 1.53]

참고 문헌

[1]Siciliano, B., Sciavicco, L., Villani, L., & Oriolo, G. (2009). Differential kinematics and statics. Robotics: Modelling, Planning and Control, 105-160.

[2]Harry Asada, and John Leonard. 2.12 Introduction to Robotics. Fall 2005. Chapter 6 Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. 라이선스: Creative Commons BY-NC-SA.

참고 항목

객체

함수