Vectors in 3-D Coordinate Systems
Vectors represent quantities such as velocity and acceleration. Mapping Toolbox™ functions transform vector components between Earth-centered Earth-fixed (ECEF) and east-north-up (ENU) or north-east-down (NED) systems. For more information about ECEF, ENU, and NED coordinate systems, see Comparison of 3-D Coordinate Systems.
Unlike coordinates that measure position, vector components in a Cartesian system do not depend on a position in space. Therefore, when you transform a vector from one system to another, only the components of the vector change. The magnitude of the vector remains the same.
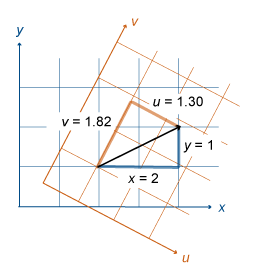
For example, this image shows a 2-D vector transformation from an x-y system to a u-v system. The vector has components x = 2 and y = 1 in the x-y system, and components u = 1.30 and v = 1.82 in the u-v system. The components of the vector are different, but in each system the magnitude of the vector is 2.24 units.
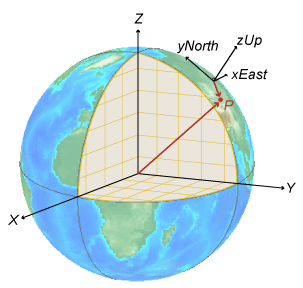
This image shows a coordinate transformation from a global ECEF system to a local ENU
system using ecef2enu. The position vectors start at the origin
of each system and end at point P. Therefore, the transformation changes
the magnitude of the position vector.
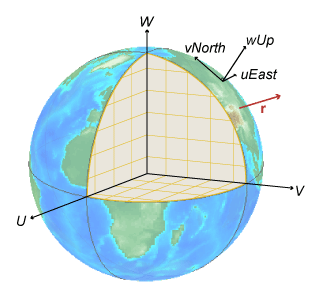
This image shows a vector transformation from a global ECEF system to a local ENU system
using ecef2enuv. The vector r does not depend on a position. Therefore, the transformation changes the
components of the vector, but the magnitude of the vector is the same.
Tips
Unlike coordinate transformation functions such as ecef2enu, vector transformation functions such as ecef2enuv do not require you to specify a reference spheroid or the
ellipsoidal height of the local origin. The geodetic latitude and longitude of the local
origin is sufficient to define the orientation of the uEast,
vNorth, and wUp axes.
See Also
enu2ecefv | ned2ecefv | ecef2nedv | ecef2enuv