Vectorize the Objective and Constraint Functions
Vectorize for Speed
Direct search often runs faster if you vectorize the
objective and nonlinear constraint functions. This means your functions
evaluate all the points in a poll or search pattern at once, with
one function call, without having to loop through the points one at
a time. Therefore, the option UseVectorized = true works
only when UseCompletePoll or UseCompleteSearch is
also set to true. However, when you set UseVectorized = true, patternsearch checks
that the objective and any nonlinear constraint functions give outputs
of the correct shape for vectorized calculations, regardless of the
setting of the UseCompletePoll or UseCompleteSearch options.
If there are nonlinear constraints, the objective function and the nonlinear constraints all need to be vectorized in order for the algorithm to compute in a vectorized manner.
Note
Write your vectorized objective function or nonlinear constraint
function to accept a matrix with an arbitrary number of points. patternsearch sometimes
evaluates a single point even during a vectorized calculation.
Vectorized Objective Function
A vectorized objective function accepts a matrix as input and
generates a vector of function values, where each function value corresponds
to one row or column of the input matrix. patternsearch resolves
the ambiguity in whether the rows or columns of the matrix represent
the points of a pattern as follows. Suppose the input matrix has m rows
and n columns:
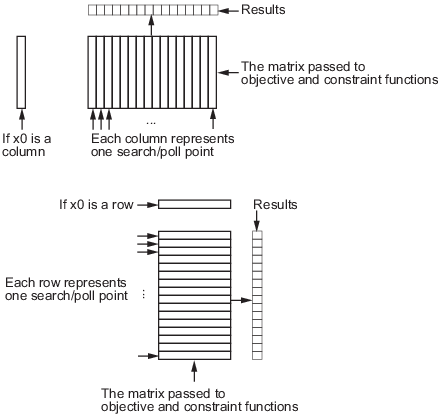
If the initial point
x0is a column vector of sizem, the objective function takes each column of the matrix as a point in the pattern and returns a row vector of sizen.If the initial point
x0is a row vector of sizen, the objective function takes each row of the matrix as a point in the pattern and returns a column vector of sizem.If the initial point
x0is a scalar,patternsearchassumes thatx0is a row vector. Therefore, the input matrix has one column (n= 1, the input matrix is a vector), and each entry of the matrix represents one row for the objective function to evaluate. The output of the objective function in this case is a column vector of sizem.
Pictorially, the matrix and calculation are represented by the following figure.
Structure of Vectorized Functions
For example, suppose the objective function is
If the initial vector x0 is
a column vector, such as [0;0], a function for
vectorized evaluation is
function f = vectorizedc(x)
f = x(1,:).^4+x(2,:).^4-4*x(1,:).^2-2*x(2,:).^2 ...
+3*x(1,:)-.5*x(2,:);x0 is a row vector, such as [0,0],
a function for vectorized evaluation isfunction f = vectorizedr(x)
f = x(:,1).^4+x(:,2).^4-4*x(:,1).^2-2*x(:,2).^2 ...
+3*x(:,1)-.5*x(:,2);Tip
If you want to use the same objective (fitness) function for
both pattern search and genetic algorithm, write your function to
have the points represented by row vectors, and write x0 as
a row vector. The genetic algorithm always takes individuals as the
rows of a matrix. This was a design decision—the genetic algorithm
does not require a user-supplied population, so needs to have a default
format.
To minimize vectorizedc, enter the following commands:
options=optimoptions('patternsearch','UseVectorized',true,'UseCompletePoll',true);
x0=[0;0];
[x,fval]=patternsearch(@vectorizedc,x0,...
[],[],[],[],[],[],[],options)MATLAB® returns the following output:
Optimization terminated: mesh size less than options.MeshTolerance.
x =
-1.5737
1.0575
fval =
-10.0088Vectorized Constraint Functions
Only nonlinear constraints need to be vectorized; bounds and linear constraints are handled automatically. If there are nonlinear constraints, the objective function and the nonlinear constraints all need to be vectorized in order for the algorithm to compute in a vectorized manner.
The same considerations hold for constraint functions as for
objective functions: the initial point x0 determines
the type of points (row or column vectors) in the poll or search.
If the initial point is a row vector of size k,
the matrix x passed to the constraint function
has k columns. Similarly, if the initial point
is a column vector of size k, the matrix of poll
or search points has k rows. The figure Structure of Vectorized Functions may make
this clear. If the initial point is a scalar, patternsearch assumes
that it is a row vector.
Your nonlinear constraint function returns two matrices, one
for inequality constraints, and one for equality constraints. Suppose
there are nc nonlinear inequality
constraints and nceq nonlinear
equality constraints. For row vector x0, the constraint
matrices have nc and nceq columns
respectively, and the number of rows is the same as in the input matrix.
Similarly, for a column vector x0, the constraint
matrices have nc and nceq rows
respectively, and the number of columns is the same as in the input
matrix. In figure Structure of Vectorized Functions, “Results”
includes both nc and nceq.
Example of Vectorized Objective and Constraints
Suppose that the nonlinear constraints are
Write a function for these constraints for row-form x0 as
follows:
function [c ceq] = ellipsecosh(x) c(:,1)=x(:,1).^2/9+x(:,2).^2/4-1; c(:,2)=cosh(x(:,1))-x(:,2)-1; ceq=[];
Minimize vectorizedr (defined in Vectorized Objective Function) subject to the constraints
ellipsecosh:
x0=[0,0];
options = optimoptions('patternsearch','UseVectorized',true,'UseCompletePoll',true);
[x,fval] = patternsearch(@vectorizedr,x0,...
[],[],[],[],[],[],@ellipsecosh,options)MATLAB returns the following output:
Optimization terminated: mesh size less than options.MeshTolerance and constraint violation is less than options.ConstraintTolerance. x = -1.3516 1.0612 fval = -9.5394