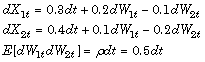interpolate
Brownian interpolation of stochastic differential equations (SDEs) for
SDE, BM, GBM,
CEV, CIR, HWV,
Heston, SDEDDO, SDELD, or
SDEMRD models
Description
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
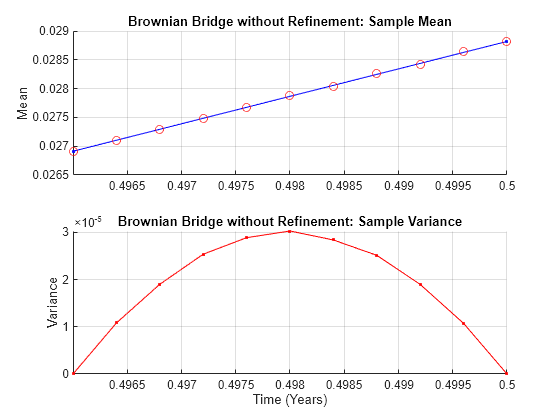
This function performs a Brownian interpolation into a user-specified time series array, based on a piecewise-constant Euler sampling approach.
Consider a vector-valued SDE of the form:
where:
X is an NVars-by-
1state vector.F is an NVars-by-
1drift-rate vector-valued function.G is an NVars-by-NBrowns diffusion-rate matrix-valued function.
W is an NBrowns-by-
1Brownian motion vector.
Given a user-specified time series array associated with this equation, this function performs a Brownian (stochastic) interpolation by sampling from a conditional Gaussian distribution. This sampling technique is sometimes called a Brownian bridge.
Note
Unlike simulation methods, the interpolation function does not
support user-specified noise processes.
The
interpolatefunction assumes that all model parameters are piecewise-constant, and evaluates them from the most recent observation time inTimesthat precedes a specified interpolation time inT. This is consistent with the Euler approach of Monte Carlo simulation.When an interpolation time falls outside the interval specified by
Times, a Euler simulation extrapolates the time series by using the nearest available observation.The user-defined time series
Pathsand corresponding observationTimesmust be fully observed (no missing observations denoted byNaNs).The
interpolatefunction assumes that the user-specified time series arrayPathsis associated with thesdeobject. For example, theTimesandPathsinput pair are the result of an initial course-grained simulation. However, the interpolation ignores the initial conditions of thesdeobject (StartTimeandStartState), allowing the user-specifiedTimesandPathsinput series to take precedence.
References
[1] Aït-Sahalia, Y. “Testing Continuous-Time Models of the Spot Interest Rate.” The Review of Financial Studies, Spring 1996, Vol. 9, No. 2, pp. 385–426.
[2] Aït-Sahalia, Y. “Transition Densities for Interest Rate and Other Nonlinear Diffusions.” The Journal of Finance, Vol. 54, No. 4, August 1999.
[3] Glasserman, P. Monte Carlo Methods in Financial Engineering. New York, Springer-Verlag, 2004.
[4] Hull, J. C. Options, Futures, and Other Derivatives, 5th ed. Englewood Cliffs, NJ: Prentice Hall, 2002.
[5] Johnson, N. L., S. Kotz, and N. Balakrishnan. Continuous Univariate Distributions. Vol. 2, 2nd ed. New York, John Wiley & Sons, 1995.
[6] Shreve, S. E. Stochastic Calculus for Finance II: Continuous-Time Models. New York: Springer-Verlag, 2004.
Version History
Introduced in R2008a