Hadamard Code Generator
Generate Hadamard code from orthogonal set of codes
Library
Sequence Generators sublibrary of Comm Sources
Description
The Hadamard Code Generator block generates a Hadamard code from a Hadamard matrix, whose rows form an orthogonal set of codes. Orthogonal codes can be used for spreading in communication systems in which the receiver is perfectly synchronized with the transmitter. In these systems, the despreading operation is ideal, as the codes are decorrelated completely.
The Hadamard codes are the individual rows of a Hadamard matrix. Hadamard matrices are square matrices whose entries are +1 or -1, and whose rows and columns are mutually orthogonal. If N is a nonnegative power of 2, theN-by-N Hadamard matrix, denoted HN, is defined recursively as follows.
The N-by-N Hadamard matrix has the property that
HNHNT = NIN
where IN is the N-by-N identity matrix.
The Hadamard Code Generator block outputs a row of HN. The output is bipolar. You specify the length of the code, N,by the Code length parameter. The Code length must be a power of 2. You specify the index of the row of the Hadamard matrix, which is an integer in the range [0, 1, ... , N-1], by the Code index parameter.
Parameters
- Code length
A positive integer that is a power of two specifying the length of the Hadamard code.
- Code index
An integer between 0 and N-1, where N is the Code length, specifying a row of the Hadamard matrix.
- Sample time
Positive scalars specify the time in seconds between each sample of the output signal. If you set the sample time to
-1, the output signal inherits the sample time from downstream. For information on the relationship between the Sample time and Samples per frame parameters, see Sample Timing.- Samples per frame
Samples per frame, specified as a positive integer indicating the number of samples per frame in one channel of the output data. For information on the relationship between Sample time and Samples per frame, see Sample Timing.
- Output data type
The output type of the block can be specified as an
int8ordouble. By default, the block sets this todouble.- Simulate using
Select the simulation mode.
Code generationOn the first model run, simulate and generate code. If the structure of the block does not change, subsequent model runs do not regenerate the code.
If the simulation mode is
Code generation, System objects corresponding to the blocks accept a maximum of nine inputs.Interpreted executionSimulate model without generating code. This option results in faster start times but can slow subsequent simulation performance.
Examples
Orthogonal Spreading for Multiuser System in Single-Path Channel
This model compares data recovery for a single-user system versus a two-user system. Transmission data passes through a single-path AWGN channel in two data streams that are independently spread by different orthogonal codes.
The model uses random binary data, which is BPSK modulated (real), spread by orthogonal codes of length 64, and then transmitted over an AWGN channel. The receiver consists of a despreader followed by a BPSK demodulator.
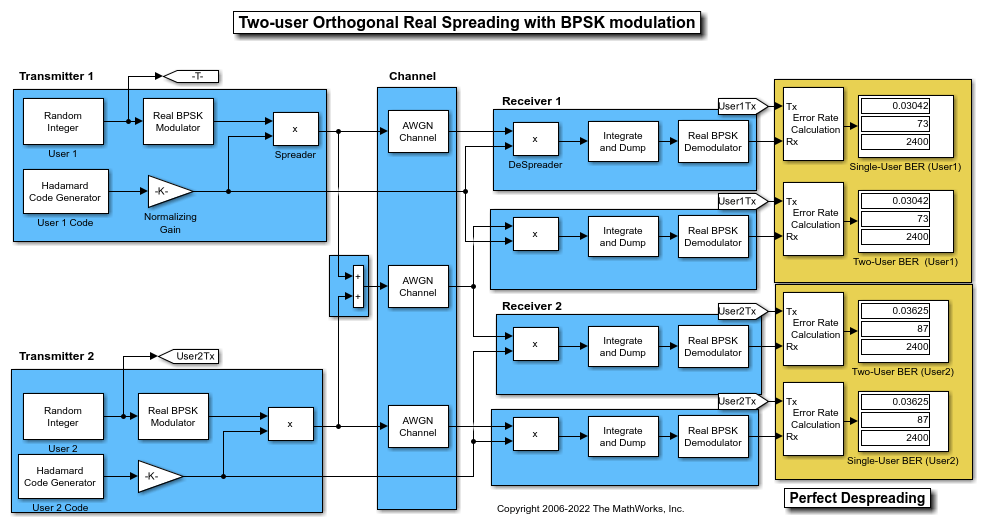
Using the same transmission data, the model calculates the BER performance for recovery of the single-user and two-user transmissions through identically configured AWGN channels.
The bit error rate results are exactly the same for the individual users in both cases. The matching error rates result from perfect despreading due to the ideal cross-correlation properties of the orthogonal codes selected.
To experiment further, open the model. Modify the settings to see how the performance varies with different Hadamard codes for the individual users.
Orthogonal Spreading for Single-User System in Multipath Channel
This model simulates orthogonal spreading for a single-user system in a multipath transmission environment. This is similar to a mobile channel environment where the signals are received over multiple paths. Each path can have different amplitudes and delays. The receiver combines the independent paths coherently by using diversity reception to realize gains from the multipath transmissions received. The modeled system does not simulate fading effects and the receiver gets perfect knowledge of the number of paths and their respective delays.
The model uses random binary data, which is BPSK modulated (real), spread by orthogonal codes of length 64, and then transmitted over a multipath AWGN channel. The receiver consists of a despreader, a diversity combiner, and a BPSK demodulator.

The non-ideal, auto-correlation values of the chosen orthogonal spreading codes prevent perfect resolution of the individual paths. As a consequence, BER performance is not improved by using diversity combining in the receiver. For a multipath example that uses PN sequences when spreading user data and uses diversity combining in the receiver, see PN Spreading for Single-User System in Multipath Channel.
To experiment further, open the model. Modify the settings to see how the performance varies for different path delays or with different Hadamard codes.