comm.GMSKModulator
Modulate using GMSK method
Description
The comm.GMSKModulator
System object™ modulates using the Gaussian minimum shift keying (GMSK) method. The output is a
baseband representation of the modulated signal. For more detail, see Algorithms.
To modulate a signal by using the GMSK method:
Create the
comm.GMSKModulatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
gmskmodulator = comm.GMSKModulator
gmskmodulator = comm.GMSKModulator(Name,Value)comm.GMSKModulator(PulseLength=6)
specifies the length of the Gaussian pulse shape as 6 symbol intervals.
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
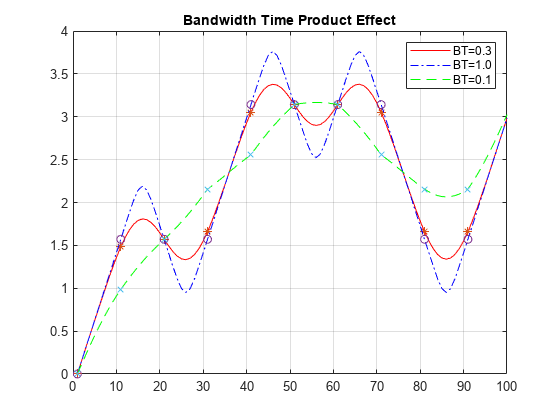
The BandwidthTimeProduct
property represents the bandwidth multiplied by time. Use this property to reduce the
bandwidth at the expense of increased intersymbol interference. The PulseLength property measures the length of the Gaussian pulse shape in symbol
intervals. These equations define the frequency pulse shape.
Bb represents the bandwidth of the pulse and
T is the symbol durations. Q(t) is the complementary
cumulative distribution function.
For this System object, an input symbol of 1 causes a phase shift of π/2 radians, which corresponds to a modulation index of 0.5.
References
[1] Anderson, John B., Tor Aulin, and Carl-Erik Sundberg. Digital Phase Modulation. New York: Plenum Press, 1986.